一类时间模上的半线性脉冲方程的振荡问题

2017-06-23宋里宏李耀红

宿州学院学报 2017年4期

关键词：宿州时滞序号

芦伟,宋里宏,李耀红

1.宿州学院数学与统计学院，宿州，234000；2.海军航空工程学院7系，烟台，264001

一类时间模上的半线性脉冲方程的振荡问题

芦伟1,宋里宏2,李耀红1

1.宿州学院数学与统计学院，宿州，234000；2.海军航空工程学院7系，烟台，264001

本文研究了带阻尼项的时间模上的半线性脉冲时滞动力方程:

的振荡性问题，通过使用一个特殊的脉冲不等式和Riccati技巧，得到此类方程解的振荡性的若干判定准则，并通过例子验证了结论的实际意义。

时间模；脉冲；半线性；时滞；振荡性

近年来，对微分方程振荡理论的研究与应用几乎渗入所有学科和应用领域，尤其是时间模上的动力方程的研究广泛出现在工业控制理论、生物数学模型、电磁理论、神经系统理论等领域[1-18]。脉冲的引入为时间模上的动力方程的研究提出了新的课题[3]。本文讨论如下带阻尼项的分数阶脉冲时滞方程：

(1)

(2)

(H2)F(t),f(t):C(T→R)且uF(u)>0,uf(u)>0；

(H3)δ(t),θ(t):T→T满足δ(t)≤t,θ(t)≤t,limt→∞δ(t)=+∞,limt→∞θ(t)=+∞；

(H4)存在正常数L,κ使得F(u)/u≥L,f(u)/u≤κ(u≠0)且φ(t)=Lp(t)-κq(t)>0；

(H6)F(t):C1(T→R)满足对所有的不为零的变量u有F′(u)>0，对任意ab>0有F(ab)≥F(a)F(b)。

本文使用的时间模上的微积分基本概念参见文献[1-2]。

近年来，研究时间模上动力方程的振荡性问题已有较多的成果[4-18],而对时标上脉冲型动力方程的研究并不深入。文献[15]和[16]研究了非线性项带σ(t)的特殊情况，得出了一些判定振荡性的充分条件，本人在此基础上进一步推广振荡问题的研究，并考虑多时滞的影响，较之文献[18]考虑更为一般的方程，并且使用积分平均技巧和一个特殊的不等式，因此得到的结果具有一定的理论意义。

1 主要结果

下面使用积分平均技巧建立方程(1)的如下类型的振荡定理，为此，假设在域Ω:={(t,s):t≥s≥t0}上，存在函数H,H′s∈C1(Ω,R)，满足：

H(t,t)=0,t≥t0,H(t,s)>0,H′s(t,s)≤0,t>s≥t0

(3)

则当t≥t0时，有：

(4)

引理2[2]假设g∈R+，即g∈Crd(T，R)并且对于任意的tk,t∈[t0,+∞]T，满足1+μ(t)g(t)>0，则初值问题yΔ(t)=g(t)y(t),y(t0)=y0∈R在[t0,+∞]T上有唯一的正解eg(t,t0)，也记为eg(·,t0)，它满足半群性质eg(a,b)eg(b,c)=eg(a,c)。

引理3[19]假设X和Y都是非负数，则有：

Xλ+(λ-1)Y-λXYλ-1≥0,λ>1

当且仅当X=Y时等式成立。

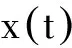
(5)

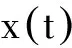
(6)

根据引理2和(6)式，对t∈(tk,tk+1]T,k=1,2,3,…，又可得到：

(7)

(8)

(9)

(10)

(11)

则方程(1)是振荡的。

证明设x(t)是方程(1)在[t0,∞)T上的一个非振荡解，不失一般性，可假设x(t)是方程(1)的最终正解(x(t)是方程(1)的最终负解可类似证明)，不妨设当t≥T≥t0时x(t)>0，由定理的条件知引理4成立。下面定义广义的Riccati变换：

由引理4知，当t≥T≥t0时，w(t)>0,又：

(12)

根据xΔ(t)和A(t)(xΔ(t))γ的单调性知，当t>tk>T时：

A(t)(xΔ(t))γ≤A(σ(t))(xΔ(σ(t)))γ,x(σ(t))≥x(t)

(13)

将(13)式代入(12)式得：

(14)

使用时间模上指数函数微分的链式法则[2]得：

(15)

(16)

(17)

由(16)和(17)得到：

(18)

移项并以s代替t得：

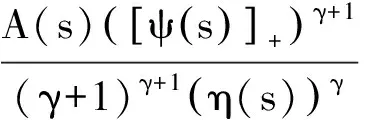
(19)

(19)式两边同乘以H(t,s)，并对s在t>s>tk≥t1上进行分段积分，则：

(20)

再由条件(H5)知，对t∈(tk,tk+1],k=1,2,…有：

(21)

使用分部积分法可推出对所有的t>s>tk≥t1>T都有：

(22)

将(22)带入(20)得：

因此

(23)

从而

(24)

这与条件(11)发生矛盾，因此方程(1)是振荡的。证毕。

定理2 假设(H1)～(H5)和(5)成立,并且假设：

(25)

这里[ψ(t)]+如定理1一样定义，则方程(1)是振荡的。

(26)

(27)

根据引理1可知：

(28)

取t→∞时由条件(25)知(28)式的右端小于零，这与w(t)>0相矛盾。命题得证。

接下来考虑当f(t)=0,F′(t)>0时方程(1)的振荡定理。

定理3 假设(H1)～(H6)和条件(5)成立，并且进一步假设：

(29)

则方程(1)的解是振荡的。

证明设x(t)是方程(1)的一个非振荡解，不失一般性，假设x(t)>0最终成立，沿袭引理4的证明，可以得到x(t)>0,xΔ(t)>0,t∈(tk,tk+1]T,tk>t0,k=1,2,…，

(30)

(31)

根据(H3)(H4)(H5)可以看出：

(32)

使用引理1可得：

(31)

根据条件(29)，式(31)右端当t→∞时为负，这与w(t)>0矛盾。命题得证。

2 例子

例1 考虑方程：

(32)

不难验证条件(H2)(H3)(H5)满足，取L=1易看出(H4)满足。

所以条件(5)被满足。又因为：

根据定理3得方程(32)是振动的。

例2 考虑方程：

(33)

3 结论

考虑的时间模上的脉冲动力方程较以往的脉冲动力方程更加一般化，同时还考虑了双时滞的影响和二阶项系数函数的脉冲问题。定理的结果可涵盖非时滞方程的情况并且对脉冲的影响又加以说明，因此本文的结果是对已有定理的进一步推广,并且更加细致和新颖。脉冲振动的判定准则可作为桥梁、轮船甲板等材料耐受力的检测工具，因此本文所研究的问题又具有很好的实际应用意义。

[1]PRavi,RPAgarwal,MBohner，etal.Nonoscillationandoscillation:Theoryforfunctionaldifferentialedquations[M].NewYork:MarcelDekker,2004:377-717

[2]MBohner,APeterson.DynamicEquationsonTimeScales:AnIntroductionwithApplication[M].Boston：Birkhaser,2001:3-155

[3]RPAgarwal,MBenchohra,DO’ReganA.Ouahab.Secondorderimpulsivedynamicequationsontimescales[J].FunctDifferEqu,2004,11:223-234

[4]VLakshmikantham,DDBainov,PSSimeonov.TheoryofImpulsiveDifferentialEquations[M].Singapore：WorldScientific,1989:1-288

[5]EABohner,JHoffacker.OscillationpropertiesofanEmden-Fowlertypeequationondiscretetimescales[J].JDifferenceEquAppl,2003,9:602-612

[6]AZafer.Onoscillationandnonoscillationofsecond-orderdynamicequations[J].AppliedMathematicsLetters,2009,22:136-141

[7]SHSaker.Oscillationcriteriaofsecond-orderhalf-lineardynamicequationsontimescales[J].JComputApplMath,2005,177:375-387

[8]SSun,ZHan,CZhang.Oscillationofsecondorderdelaydynamicequationsontimescales[J].JApplMathComput,2009,30:459-468

[9]SRGrace,MBohner,RPAgarwal.Ontheoscillationofsecond-orderhalf-lineardynamicequations[J].JDifferenceEquAppl,2009,15(5):451-460

[10]ZHan,TLi,SSun,CZhang.Oscillationforsecond-ordernonlineardelaydynamicequationsontimescales[J].AdvDifferEqu,2009(9):1-13

[11]QZhang,LGao,LWang.Oscillationofsecond-ordernonlineardelaydynamicequationsontimescales[J].ComputMathAppl,2011,61:2342-2348

[12]QZhang.Oscillationofsecond-orderhalf-lineardelaydynamicequationswithdampingontimescales[J].JComputApplMath,2011,235:1180-1188

[13]JiashanYang,XuewenQin.Oscillationcriteriaforcertainsecond-orderEmden-Fowlerdelayfunctionaldynamicequationswithdampingontimescales[J].AdvDifferenceEqu,2015:1-16

[14]MBenchohra,SHamani,JHenderson.Oscillationandnonoscillationforimpulsivedynamicequationsoncertaintimescales[J].AdvDifferenceEqu，2006(6):1-12

[15]MugenHuang.Oscillationcriteriaforsecondordernonlineardynamicequationswithimpulses[J].ComputersandMathematicswithApplications,2010,59:31-41

[16]MugenHuang,WeizhenFeng.Oscillationcriteriaforimpulsivedynamicequationsontimescales[J].ElectronJDifferentialEquations，2007,169:1-9

[17]杨甲山，谭伟明，覃学文，等.时间模上二阶非线性阻尼动力方程的振动性分析[J].浙江大学学报:理学版,2016,43(1):64-70

[18]芦伟，葛渭高.时标上二阶脉冲阻尼动力方程解的振动性和渐近性[J].生物数学学报，2013,28(2)：343-349

[19]GHHardy,JELittlewood,GPlya.Inequalities[M].Cambridge,UK：CambridgeUniversityPress,1988:1-314

(责任编辑：汪材印)

几种常见参考文献的著录格式

一、专著

[序号]主要责任者.文献题名[文献类型标识].出版地：出版者，出版年.起止页码.

例：[1]范琳，周红.二语语篇阅读推理的心理学研究[M].北京：北京大学出版社，2011:3

二、期刊文章