弹箭滚转姿态地磁测角仪的卡尔曼滤波算法

田利伟,陈国光,孙汉琴,杨 东,白敦卓

(1 中北大学机电工程学院,太原 030051;2 豫西工业集团有限公司,河南南阳 473000)

弹箭滚转姿态地磁测角仪的卡尔曼滤波算法

田利伟1,陈国光1,孙汉琴1,杨 东2,白敦卓2

(1 中北大学机电工程学院,太原 030051;2 豫西工业集团有限公司,河南南阳 473000)

为降低地磁测角仪测量地磁场矢量信息解算弹箭滚转姿态角误差,文中运用卡尔曼滤波算法对弹体滚转角进行估计。通过对火箭弹滚转角速度变化规律的分析,用二阶近似表达弹体滚转运动规律作为卡尔曼滤波算法的系统方程,以磁场强度与数字量输出之间的非线性关系作为卡尔曼滤波算法的量测模型。通过实验仿真分析结果表明,滤波所得弹体滚转角、滚转角速度精度满足弹道修正弹要求,可用于弹道修正弹药被动段的弹道控制。

地磁测角仪;卡尔曼滤波算法;弹箭滚转角测量

0 引言

弹道修正弹箭系统中,滚转角的实时测量是实施弹道修正控制的先决条件。弹体滚转角测量的方法多种多样,而地磁测量法是恰当、经济、稳定并有适用精度的方法。地磁法的一般过程为:利用全球地磁模型[1-2]、当地的地磁图或测量仪器,获得当地的地磁场七要素;在射击诸元准备阶段,利用弹道计算软件获得弹箭速度矢量随时间的变化曲线,也可根据弹道方案的需要,进一步计算出地磁场矢量在弹轴坐标系下三分量随时间的变化曲线;用磁传感器敏感地磁分量,经放大后进一步数字化,解出地磁场矢量在测量坐标系下的方位角;用提前测取的基准对其参数校准,解出弹体滚转角。在整个测量过程中地磁组建安装误差角、器件参数随环境温度变化、其他随机的噪声等不良因素的影响,难以实现弹体滚转角度的高精度测量。为了实现对滚转角度的高精度测量,文中以量测的数字量与地磁场强度的非线性关系为量测方程,以弹体滚转角的二阶近似作为系统方程进行滤波。滤波结果所得的弹体滚转角、滚转角速度与理想弹道模型样本分别进行比较,并给出相应的滤波精度图。通过仿真实验结果表明滤波处理能够降低随机噪声、环境因素等对量测地磁矢量解算弹体滚转角的影响,可用于弹道修正类弹药被动段的弹道控制过程。

1 火箭弹滚转运动

由外弹道学理论可知弹体滚转角速度的动力学方程[3]:

(1)

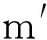
根据弹箭飞行的轨迹、速度的一般规律,分析式(1)可知:弹丸飞行速度爬升、高度增加弹箭角速度在导转力矩和极阻尼力矩作用下在主动段快速升高,其后,缓慢下降。在降弧段随着弹丸速度和空气密度增加,角速度稍有回升。

图1是一种典型的火箭弹滚转角速度变化规律。

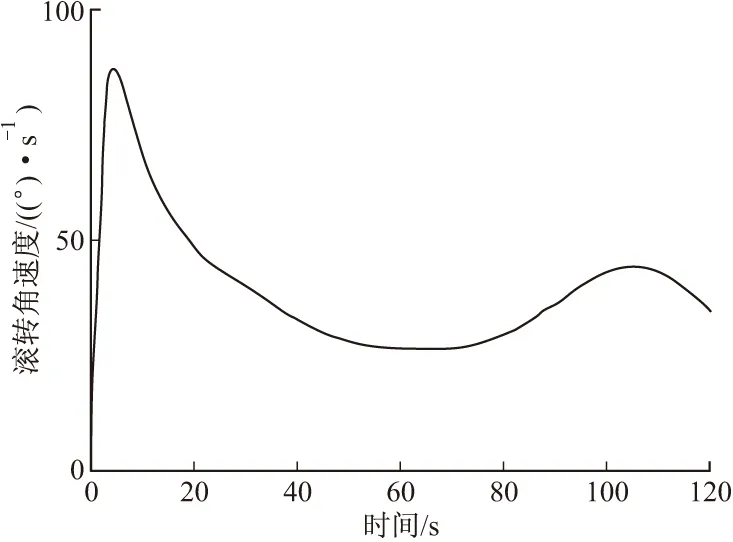
图1 弹箭滚转角速度

2 地磁信号的数字化

基地磁组件测量磁场强度解算弹体滚转过程是正交双轴磁强计感应磁场强度,输出相应的微弱电压。将磁传感器输出信号经放大器、跟随器调理后,由AD转换器将电压模拟信号转换为数字信号,并对该数字信号进行适当速率的数据采集。

通过进一步分析归纳,发现水边植物群落评分结果与驳岸的硬质化程度有明显关系,而建筑周边植物群落得分与植物群落所处的位置有明显的相关性(图4)。

Ny=Ny0+kyhsinγ

Nz=Nz0+kzhcosγ

(2)

或

Ny=Ny0+Aysinγ

Nz=Nz0+Azcosγ

(3)

式中:Ny0、Nz0为信号基线;ky、kz为灵敏度;h为弹体横截面磁场强度分量;γ为弹体滚转角;Ay、Az为输出信号幅值。

3 地磁测角仪的卡尔曼滤波

实际工作环境中,信号基线Ny0、Nz0灵敏度ky、kz因环境温度的差异而有变动。弹丸在飞行过程中弹轴与地磁场矢量夹角时刻发生变化,数字信号的幅值Ay、Az也发生相应的变化。信号基线Ny0、Nz0和幅值Ay、Az直接影响数字量输出,数字量输出精度,决定解算弹体滚转角精度所以需要对信号基线、幅值进行最优估计。数字化的地磁矢量信号Ny、Nz

双轴弹载地磁组件的数字输出与弹体横截面磁场强度分量h的关系如下[4-5]:

（4）酒店机电安装专业多、专业性强、整体协调质量管理难度大：酒店机电工程包括管道工程、通风工程、强电系统、弱电系统、给排水系统等，不同专业关联性、系统性极强，并与精装饰整体协调质量难度大。

一步预测方程:

Xk+1=Φk+1,kXk+ΓkWk

(4)

式中:Φk+1,k为tk时刻至tk+1时刻的一步转移阵;Γk为系统的噪声驱动矩阵;Wk为系统噪声序列。

状态转移矩阵:

在启动滤波器递推算法之前,对弹体滚转一定周期内两轴输出的数字量进行平滑估计。平滑结果如图3所示,通过搜索算法获取平滑结果中y、z两轴数字量的最大值Ny,max、Nz,max和最小值Ny,min、Nz,min。

x是待优化的相机内外参数，c是代价函数，L是损失函数。对于重构过程中的优化调整，代价函数为点云中三维点通过相机内外参数计算投影到图像的像素坐标与该三维点所对应实际像素坐标之间的差值，由于c的返回值为一个表示误差的向量（图像齐次坐标差值），故取该向量的2范式作为总体的代价。而最小化这个误差则可视作是一个优化相机内外参数和点云数据的过程。设Ki，[Ri|Ti]分别表示图像i的内参矩阵和外参矩阵[8]，点云中某点三维坐标为Pj，并与之在图像上对应像素坐标，投影误差则表示为式（15）

系统噪声序列:

治愈:患者咳嗽、咳痰、气短、体温等临床症状均恢复正常,肺部啰音消失,影像学检查肺部炎症全部吸收,外周血白细胞计数恢复正常;好转:患者咳嗽、咳痰、气短、体温等临床症状均减轻,肺部啰音好转,影像学检查肺部炎症大部分吸收;无效:患者临床症状及体征无任何改变甚至加重[7]。治疗有效率=治愈率+好转率。

最优状态向量估计:

Qk为系统噪声序列的方差矩阵,且:

根据双轴弹载地磁组件的数字输出与弹体横截面上磁场强度分量的关系,量测向量Z的量测方程为:

(5)

由于卡尔曼滤波针对的是线性方程,需要对上式进行线性化。线性化如下:

Zk=HkXk+Vk

(6)

式中:

(7)

信号基线的初始值计为Ny0、Nz0,信号基线初始值与搜索算法获取最大值最小值的关系:

解码器的构建。解码器可以有多种不同的配置。通过对HDecode的实验，得出最优参数为：字插入代价为0、语言模型的权重为10、修剪阈值为150。总结出的Julius评估的解码参数如表4所示。表4中的参数值增加了计算资源的使用，减缓了解码过程，但提高了识别的准确性。

本文中所说的“冰臼”、“冰壁龛”等类冰川地质遗迹现象，是否最终认定确实是冰川形成，还需要更多的证据，因为，上述地质现象的成因至今尚存在着争议，即除了“冰说”外，还存在着“壶说”、“风说”、“风雨说”等多种说法。

弹箭滚转角运动的卡尔曼滤波递推算法为[6]:

根据选取的滤波状态向量及弹体滚转角的二阶近似则状态方程如下:

(8)

协方差矩阵预测:

近日，据媒体报道，山东济南又有数十名大学生落入“培训贷”陷阱。原本是为了找工作，结果公司直接把他们的信息输入一个第三方小额贷款平台，导致每个人背上了从9800元到19800元不等的贷款。

(9)

滤波增益矩阵:

(10)

同时,Wk满足:

(11)

式中:

协方差最优估计:

(12)

4 卡尔曼滤波器初值估计

仿扩展卡尔曼滤波是递推算法,初值精度会影响滤波器的收敛速度。在实际工作环境中,为了获得较快的收敛速度和滤波精度,需要对初始值有较为准确的估计。文中对滤波初值估计如下:

式中,V(z)为z高度处水平风速；zmax为水平最大风速Vmax所在高度。Wood等提出的冲击风风剖面表达式为

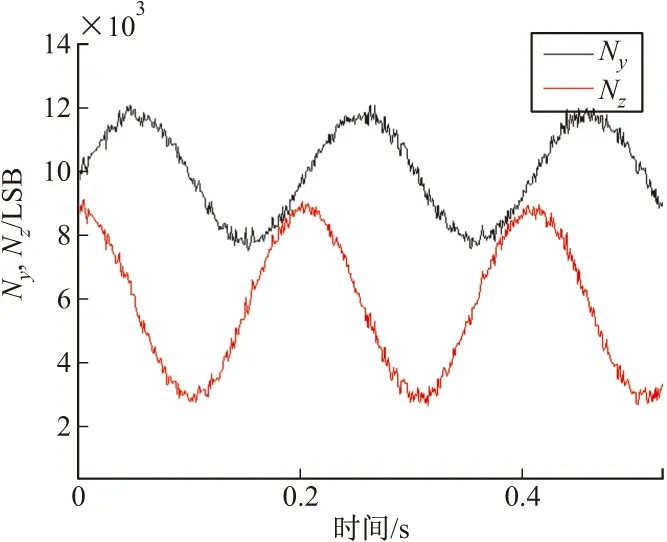
图2 起始阶段数字量输出

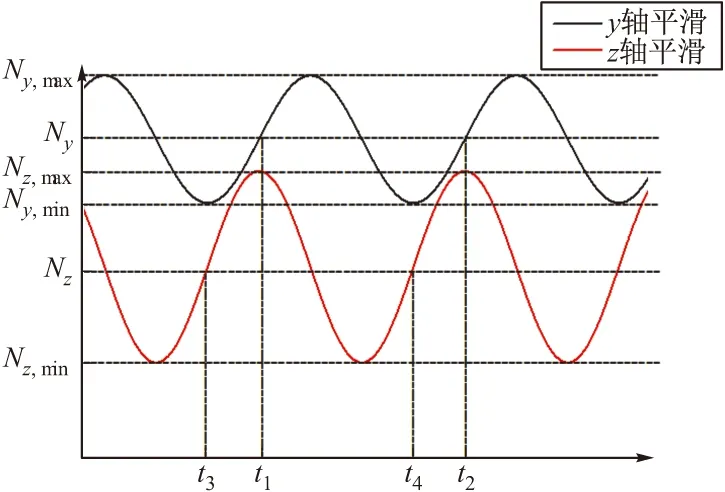
图3 数字量平滑

噪声驱动矩阵:

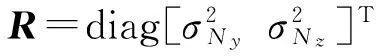
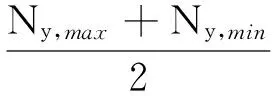
Nz0=

信号幅值的初始值计为Ay0、Az0,信号幅值的初始值与搜索算法获取最大值最小值的关系:

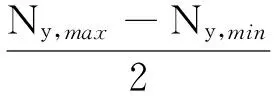
Az0=

弹体滚转角的初始值计为γ0,γ0初始值是由式(3)双轴弹载地磁组件的数字输出与弹体横截面磁场强度分量h的关系确定:

γ0=arctan

乌拉特前旗生态环境天然脆弱。辖区范围内的草原生态局部好转，整体恶化的局面并没有得到根本性转变。天然草原呈现严重恶化现象，目前，该旗已经退化的草原超过了460.28亩，占草原总面积的72.58%。草地生态环境恶化，草地生产能力退化，不仅严重影响产量，而且还会进一步影响草原生态系统的植物群落和土壤理化性质，有毒有害杂草逐渐增加，土壤生产能力逐渐下降，有机质含量不足，水土严重流失。另外，农牧民群众长期超载过量放牧，使很多天然草场、牧草资源严重被掠夺、被践踏，草地供给能力严重不足，威胁草原畜牧业健康发展。

5 仿真分析

高职院校实训基地建设要注重社会效益与经济效益的结合，建立健全实训基地管理机制，创新管理理念，采用企业管理项目管理结合的管理模式。在投资建设实训基地过程中，要多样性考虑资金投入渠道，例如学院自筹资金与政府投资、企业投资相结合，增强实训基地建设经济效益。建立健全各项规章制度，规范管理实训基地，合理配置人员，明确岗位职责，考核奖惩有度。

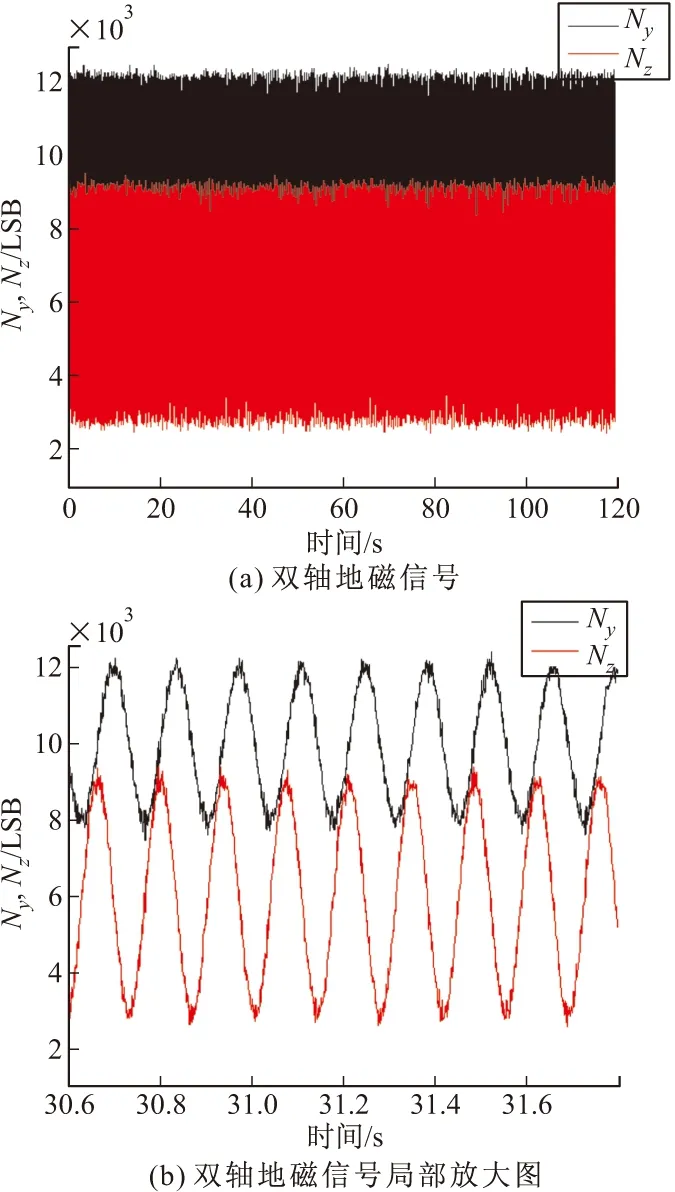
图4 地磁数字信号

图5 滚转角滤波结果

利用MDEA溶液吸收性能评价装置采集40组实验样本，其中，第1～30组数据作为训练样本用于输入BP人工神经网络预测模型进行训练，第31～40组数据作为测试样本不参加训练。当BP人工神经网络预测模型经过反复训练满足指定的容许收敛误差后，将第31～40组数据输入训练好的神经网络，比较模型预测结果与实际测试结果，见表2。

图6 滚转角滤波误差

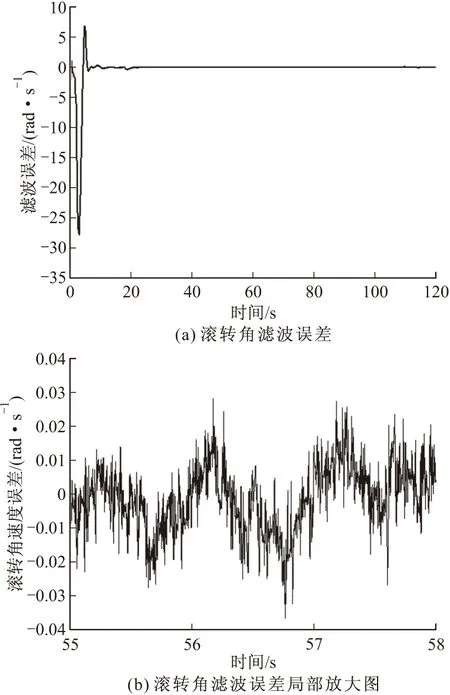
图7 滚转角速度滤波误差

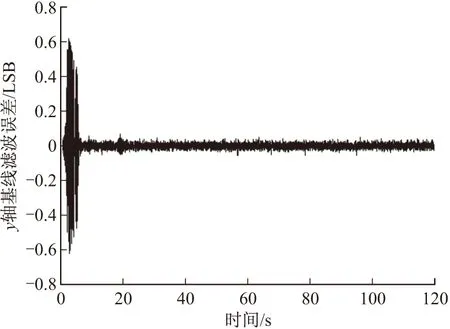
图8 y轴基线滤波误差

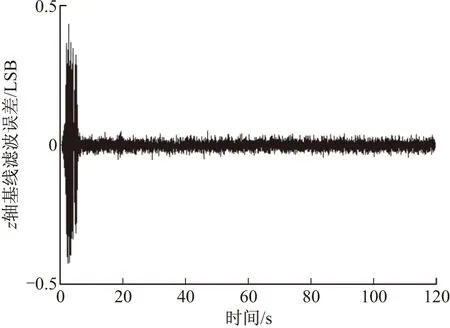
图9 z轴基线滤波误差

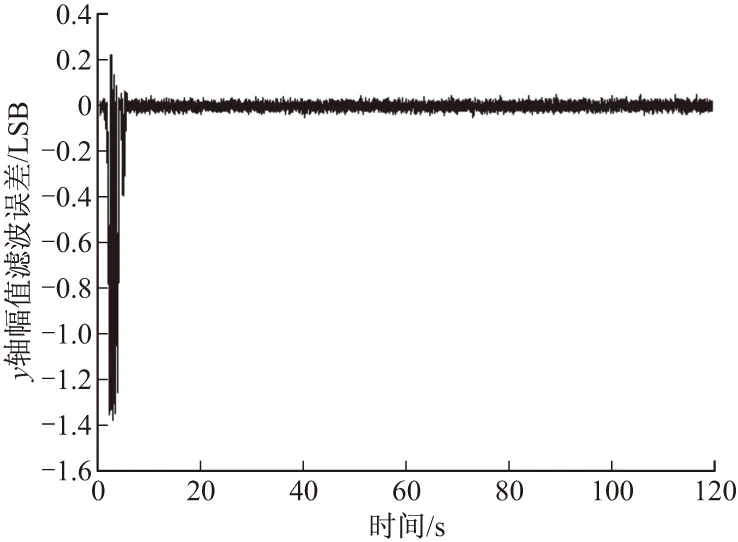
图10 y轴幅值滤波误差

6 结论

对双轴滚转角测量装置,用一阶近似扩展卡尔曼滤波算法, 可以对数字信号进行滤波处理, 有效滤除数字信号采集过程中的噪声干扰,滤波器具有较好的收敛性。当数字地磁信号噪声为2%标准差时,该算法所得弹体滚转角滤波精度在小于0.01 rad范围内(如图6所示),弹体滚转角速度滤波精度在小于0.02 rad/s范围内(如图7所示),满足弹道修正弹系统的技术要求,可用于弹道修正类弹药被动段的弹道控制过程。

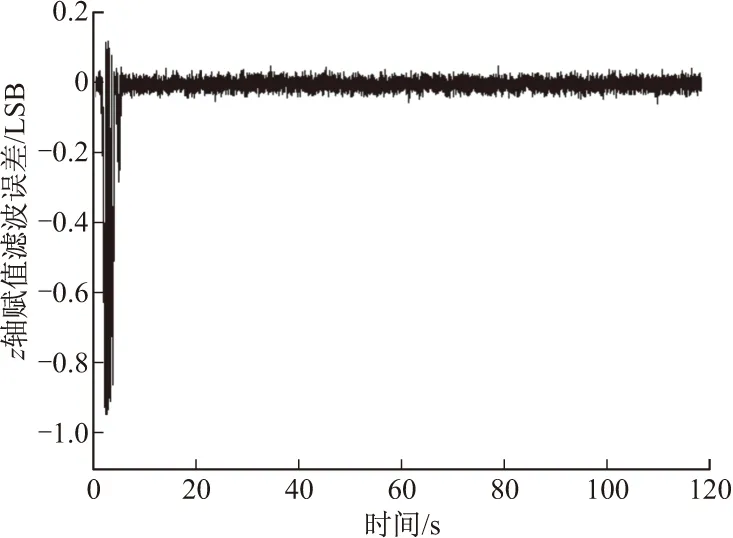
图11 z轴幅值滤波误差

[1] 李忠亮, 边少锋. 世界地磁模型WMM2010及其应用 [J]. 舰船电子工程, 2011, 31(2): 58-61.

[2] CHULLIAT A, MACMILLAN S, ALKEN P, et al. The US/UK World Magnetic Model for 2015-2020 [R]. [S.l.]: National Geophysical Data Center, 2015.

[3] 韩子鹏. 弹箭外弹道学 [M]. 北京: 北京理工大学出版社, 2008: 146-147.

[4] Magnetic Displacement Sensors HMC1501/1512 [OL]. [2016-11-11]. https: ∥aerocontent. honeywell. com/aero/common/documents/myaerospacecatalog-documents/Missiles-Munitions/HMC1501-1512.

[5] 陈铭, 辛长范, 文云, 等. 基于地磁传感器和UKF的灵巧弹药滚转估计 [J]. 弹箭与制导学报, 2012, 32(6): 83-86.

[6] 秦永元, 张洪钺, 汪叔华. 卡尔曼滤波与组合导航原理 [M]. 西安: 西北工业大出版社, 1998: 33-41.

Kalman Filtering Algorithm of Projectil Rolling Attitude Geomagnetic Goniometer

TIAN Liwei1,CHEN Guoguang1,SUN Hanqin1,YANG Dong2,BAI Dunzhuo2

(1 School of Mechatronics Engineering, North University of China, Taiyuan 030051, China; 2 Yuxi Industries Group Co. Ltd, Henan Nanyang 473000, China)

In order to reduce the geomagnetic goniometer measured magnetic field vector information solver projectile rolling attitude angle error, Kalman filtering algorithm was used to estimate the projectile rolling angle in this article. Through the analysis of the change rule of rolling angular velocity, the second order approximate expression of rolling movement law of the elastomer was used as system equations of the Kalman filtering algorithm, and the nonlinear relationship between the strength of the magnetic field and the digital output was used as the measurement model of the kalman filtering algorithm. The simulation results showed that the precision of rolling angle and rolling angular velocity obtained by filtering met the requirement of trajectory correction projectile, which could be used to control the trajectory of the trajectory correction ammunition passive segment.

geomagnetic goniometer; Kalman filtering algorithm; projectile rolling angle measurement

2016-03-29

田利伟(1990-),男,安徽阜阳人,硕士研究生,研究方向:智能弹药。

TP393

A