旋转弹箭数值虚拟飞行研究
2017-06-23梁益铭
梁益铭,康 顺
(中国兵器工业第203研究所,西安 710065)
旋转弹箭数值虚拟飞行研究
梁益铭,康 顺
(中国兵器工业第203研究所,西安 710065)
为了抑制甚至消除陀螺不稳定性以提高旋转弹箭的飞行稳定性和命中精度,采用耦合求解URANS方程和刚体运动方程组对M852弹丸和Basic Finner导弹模型进行了虚拟飞行的数值仿真,计算结果与试验结果吻合。不同的初始偏航角对M852子弹俯仰/偏航的周期影响不大,但初始偏航角越大,运动幅值越大,横向偏移越大,速度降低越快;对于低速旋转的Basic Finner模型,不同发射速度飞行特性差异较大,体现在速度演化、位移波动和锥动幅度等方面。
旋转弹箭;虚拟飞行;六自由度;M852;Basic Finner
0 引言
在飞行过程中以一定角速度旋转的弹箭称为旋转弹箭。旋转也可能诱发弹体发生陀螺不稳定和马格努斯不稳定等动态不稳定现象,严重影响弹箭的飞行距离和命中精度。为了提高旋转弹箭的飞行稳定性和命中精度,文献[1-3]等采用外弹道学理论和定常气动力参数建立了一些抑制弹体飞行不稳定性的方法。然而,在上述的动态不稳定发生与发展的过程中,必然伴随空气动力载荷的非定常演变。
目前,获得弹箭非定常空气动力学特性的技术主要有四种:1)多自由度运动风洞试验测试技术;2)基于气动靶道自由飞试验的空气动力学参数测试技术;3)基于求解URANS方程的CFD技术;4)计算流体力学(CFD)与刚体动力学(RBD)耦合数值虚拟飞行模拟技术[4]。1)、2)为实验技术,3)、4)为数值模拟技术。第一种技术试验成本高,周期长,而且受限于风洞试验段的尺度,很难测试动导数、马格努斯效应以及非定常气动特性。第二种技术是在气动靶道中进行自由飞试验,弹箭实体或者模型完全处于六自由度状态,获得弹箭空气动力参数最精确的方法,但高成本、高风险、周期长、效率低。第三种技术已经发展得非常成熟,多用于翼型震荡、弹体俯仰/偏航等过程中的非定常绕流场的研究,但公开发表的文献中少有对旋转弹箭陀螺运动过程中非定常气动特性的模拟。第四种是近几年逐渐发展起来的新的CFD技术,可以获得弹箭六自由度运动过程中详细的非定常气动力,虽然耗时长,但却是一种很有应用前景的方法,随着CFD技术的飞速发展和计算机性能的日益提高,基于CFD/RBD耦合的数值虚拟飞行模拟技术将成为研究弹箭气动与运动规律的主流技术[5-8]。
1 数值计算方法
采用CFD++软件及刚性动网格技术,耦合求解URANS方程与刚体运动方程,进行弹箭模型的六自由度虚拟飞行模拟。选用Batten-Goldberg混合RANS /LES湍流模型求解。远场边界为黎曼边界条件,固体壁面为绝热、粘性无滑移条件。
假设弹体为刚性体、弹道为无控无动力弹道、飞行过程中弹体的质量及质心均不发生变化、飞行大气条件不变。
图1为六自由度飞行的求解过程[9],假设已知n时刻流场信息Qn和弹箭的飞行姿态Pn,从n时刻到n+1时刻的求解过程为:第①步,积分Qn得到气动力参数作为刚体运动方程的输入;第②步,代入刚体运动方程求解得到弹箭n+1时刻的姿态Pn+1,并让网格随之变化;第③步,将求解得到的弹箭飞行速度、加速度、角速度和角加速度输入流动控制方程求解;第④步,通过求解流动控制方程组获得n+1时刻的流场信息Qn+1;第⑤步,重复前四步,继续下一时刻的求解,直到整个飞行过程结束。

图1 六自由度飞行的求解过程
2 M852子弹
M852子弹属于无尾翼、无控、无动力旋转弹丸。美国弹道研究实验室(BRL)[10]将它定为枪弹试验的标准模型,并且已经获得了大量与其相关的气动数据和靶道试验数据。
该子弹的重量为10.89 g,弹径为7.82 mm,质心距弹体头部的距离为19.080 8 mm,轴向惯性矩为0.722 g·cm2,横向惯性矩5.38 g·cm2(尺寸如图2所示)。

图2 M852子弹模型
计算采用结构网格,网格数目为236万。网格整体为一个O型,法向第一层网格都是5×10-6m,网格增长率为1.2,周向网格平均分布,远场为一球形远场,半径为弹长的50倍。
2.2 BRL标准工况计算
试验工况的初始转速为:ωx=-16 336.3 rad/s,ωy=-25 rad/s,初始欧拉角均为零,Ma=2.329。计算时间步长为0.01 ms。
靶道试验数据[11]提供了枪口一段距离(发射后0.02 s)子弹的俯仰偏航相位图,图3将数值计算结果与试验结果进行了对比,数值计算结果与试验结果基本吻合,能很好的捕捉子弹的运动规律,整体满足计算要求。

图3 数值计算结果与试验结果对比图
2.3 不同初始偏航角飞行对比
本小节主要研究了相同的初始转速(ωx=-16 336.3 rad/s,ωy=-25 rad/s),初始欧拉角均为0,Ma=2.329,不同初始偏航角对六自由度飞行的影响。分别对3个不同初始偏航角0°、7°以及15°进行六自由度飞行计算。计算方法、计算设置、飞行时间0.1 s和之前2.2和2.3小节选定的相同,同时考虑重力加速度。
土建工程的施工质量和人们的生命财产安全密不可分,高质量的工程会增加建筑物的寿命。因此在建筑工程施工中,应当始终严把建筑工程质量关不动摇,伴随科学的日新月异,建筑施工技术也在不断的革新,出现了很多的施工技术,大大的提升了我国土建工程的质量。
图4为M852子弹不同初始偏航旋转状态的空间姿态角变化历程对比。对于俯仰角,初始偏航角越大俯仰角振荡的幅度越大;三种初始偏航角的幅值都在衰减,有向0收敛的趋势;偏航角的变化规律和俯仰角一样。

图4 不同初始偏航角飞行俯仰/偏航角的变化历程
通过图5分析各个阶段(每隔0.025 s)不同初始偏航角的俯仰偏航相位图变化:三种初始偏航角的俯仰偏航相位图形状都如同花朵一样,这是章动与锥动运动耦合的结果。发射角越大,章动幅值较大;锥动与章动的幅值均随着时间的推移都有缩小的趋势。

图5 不同初始偏航角飞行俯仰/偏航相位的变化历程
图6是初始偏航角对高度和横向位移的影响。可以发现同样时间内,15°初始偏航角高度上升的更快、更高,0°初始偏航角高度反而下降;横向位移方面,初始偏航角越大偏移的越大,振荡的幅值越大。

图6 不同初始偏航角高度和横向偏移的变化历程
观察图7,分析初始偏航角对转速和速度的影响。转速方面,整个过程初始偏航角7°工况转速下降的最慢,0°初始偏航角最快,15°初始偏航角的转速开始阶段降低的最快,0.02 s后减慢并越来越接近7°初始偏航角的转速;速度方面,初始偏航角越大速度降低的越快。

图7 不同初始偏航角转速和速度的变化历程
3 Basic Finner导弹
3.1 计算模型与网格
Basic Finner导弹模型属于有尾翼、无控、无动力旋转导弹。由炮管发射,在膛内由高温高压的燃气使其获得出口处的速度、转速。出口转速很低,靠斜置尾翼提供滚转力矩使其加速到稳定的转速。Basic Finner为十字布局的基本带翼导弹外形,美国ARL采用Basic Finner标模进行了大量的静态气动试验和动态试验研究,已获得丰富的静态和动态试验数据以及计算数据[9-10]。尺寸如图8所示。

图8 Basic Finner导弹模型
该导弹的重量为1 589.4 g,弹径为30 mm,质心距弹体头部的距离为0.165 m,轴向惯性矩为1 924.07 g·cm2,横向惯性矩98 743.38 g·cm2。
本次计算采用的是结构网格如图9所示,网格数目为331万。网格整体为一个O型,法向第一层网格都是5×10-6m,网格增长率为1.2,周向网格平均分布,远场为一球形远场,半径为弹长的50倍。

图9 Basic Finner物面及空间网格示意图
3.2 DRDC试验工况计算
DRDC标准工况[12-13]的飞行速度为345 m/s,在音速附近,初始欧拉角均为0,初始俯仰角速度为3.5 rad/s,初始偏航角速度为0.680 7 rad/s,初始滚转角速度为-1.75 rad/s。
图10描述的是俯仰/偏航角的变化历程,计算结果和试验结果的吻合规律基本相同,在飞行距离大于100 m以后出现小范围的偏差,分析原因是由于误差累积的结果。

图10 俯仰角和偏航角随飞行距离的变化历程
从图11可以看出:在0<飞行距离<200 m,Basic Finner导弹在飞行过程中俯仰偏航相位图变化的计算结果和试验结果的相位点吻合得很好。
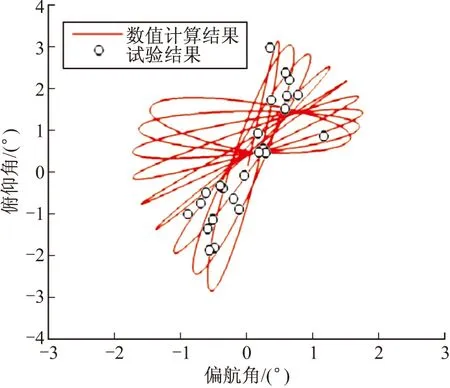
图11 俯仰偏航相位图
3.3 不同发射速度虚拟飞行计算
为了研究不同发射速度对导弹运动飞行过程中的姿态、气动参数带来的影响,本小节计算了3个不同的发射速度150 m/s、345 m/s、500 m/s分别代表亚音速、跨音速、超音速三种典型的飞行状态进行六自由度无动力飞行计算。初始欧拉角都为零,初始转速(弹轴方向)为-1.75 rad/s,初始扰动均为0。
从图12分析俯仰角的变化历程:发射速度越大,俯仰角的变化的频率越大,周期越小;在时间小于0.3 s时,发射速度越小,俯仰角的振幅越大,都有变小的趋势,而当时间大于0.3 s后,发射速度500 m/s俯仰角的振荡幅度开始增大,而发射速度150 m/s俯仰角的振幅依旧缓慢减小。同样分析偏航角的变化历程:发射速度越大,偏航角的变化的频率越大,周期越小;第一个偏航周期,发射速度越小振幅越大;发射速度345 m/s偏航角的振幅是先增大后减小的过程,而其他两个发射速度则一直保持增长趋势。再看合攻角的变化:发射速度越大,变化的周期越小;150 m/s、300 m/s发射速度的合攻角呈现出减小的趋势,而500 m/s发射速度的合攻角呈现出增大的趋势。

图12 不同发射速度俯仰角、偏航角以及合攻角的变化历程
图13给出了整个飞行过程中不同发射速度的俯仰偏航相位图的变化历程。150 m/s和345 m/s的形状相似,但是150 m/s的变化范围比345 m/s大,周期长;345 m/s发射速度,曲线的变化方向由开始的顺时针变为逆时针;500 m/s工况呈现出螺旋状增长,俯仰角的幅值逐渐增大达到了±6°,飞行开始出现失稳,弹体的马格努斯力斜率(与马赫数)相对较大(马格努斯力斜率在跨音速附近的某个马赫数区间的值非常大[10])。

图13 不同发射速度俯仰偏航相位图的变化历程
图14为导弹高度和横向偏移的变化历程:同样飞行时间,不同发射速度下降的高度基本相同,差别较小;横行偏移都是呈现出波浪式增大,发射速度越快,振荡的频率越大,周期越小,但整体的振荡幅度都在增加。

图14 不同发射速度高度、横向偏移以及飞行距离的变化历程
通过图15分析不同发射速度对导弹转速和速度带来的影响:转速方面,随着飞行的进行,转速都是先增加,然后在-60 °/m附近收敛,而且发射速度越大收敛越快;速度方面,三个发射速度受到空气阻力都有所降低,速度越快降低的斜率越大。

图15 不同发射速度转速和飞行速度的变化历程
4 结论
文中通过对M852子弹和Basic Finner导弹六自由度虚拟飞行可以得出以下结论:
1)对于高速旋转弹丸,旋转能帮助其飞行稳定。不同的初始偏航角对子弹俯仰/偏航的周期影响不大,但初始偏航角越大俯仰/偏航运动幅值越大,横向偏移越大,速度降低越快。
2)高速旋转都能帮助飞行消除初始偏航角,初始偏航角越大,消除得越慢。
3)对于低速旋转的Basic Finner,不同发射速度飞行特性差异较大,可体现在速度演化、位移波动和锥动幅度等方面,飞行速度500 m/s时,飞行失稳。
[1] 雷娟棉, 吴甲生. 尾翼稳定大长径比无控旋转火弹箭的锥形运动与抑制 [J]. 空气动力学学报, 2005, 23(4): 455-457.
[2] 任天荣, 马建敏. 基于陀螺力学的旋转导弹锥形运动分析 [J]. 宇航学报, 2010, 31(9): 2082-2087.
[3] 赵良玉, 杨树兴, 焦清介. 提高卷弧翼火箭弹圆锥运动渐近稳定性的几个方法 [J]. 固体火箭技术, 2010, 33(4): 369-372.
[4] 康顺, 党明利, 杨涛. 旋转弹箭陀螺运动非定常空气动力数值模拟研究 [C]∥航空领域动态气动力特性研讨会论文集, 2015: 483-490.
[5] 张来平, 马戒, 常兴华, 等. 虚拟飞行中气动、运动和控制耦合的数值模拟技术 [J]. 力学进展, 2014, 44: 376-417.
[6] 索谦. 基于CFD的高速旋转弹轨迹仿真 [D]. 西安: 西北工业大学, 2014.
[7] 索谦, 王刚, 李仑, 等. 基于变步长CFD/RBD方法的旋转弹轨迹仿真 [J]. 航空计算技术, 2014, 44(4): 86-90.
[8] 阎超. 基于CFD的虚拟飞行 [Z]. 北京:北京航空航天大学, 2014.
[9] 杨小亮. 飞行器多自由度耦合摇滚运动数值模拟研究 [D]. 长沙: 国防科学技术大学, 2013.
[10] MCCOY Robert L. The aerodynamic characteristics of 7.62 mm match bullets:ADA 205 633 [R]. 1988.
[11] MCCOY Robert L. Modern exterior ballistics: The luanch and flight dynamics of sysmetric projectiles [M]. Atglen:Schiffer Publishing Ltd., 2012.
[12] DUPUIS A D, HATHAWAY W. Aeroballistic range tests of the basic finner reference projectile at supersonic velocities:ADA 636 861[R]. 1997.
[13] DUPUIS A. Aeroballistic range and wind tunnel tests of the basic finner reference projectile from subsonic to high supersonic velocities: DRDC-VALCARTIER-TM-2002-136 [R].2002.
Research on Numerical Virtual Flight of Spinning Projectile
LIANG Yiming,KANG Shun
(No.203 Research Institute of China Ordnance Industries, Xi’an 710065, Chian)
In order to suppress or eliminate gyro instability to improve the flight stability and hit accuracy of spinning projectile, the numerical simulation of virtual flight of M852 projectile and Basic Finner missile model was carried out by using coupled URANS equation and rigid motion equations. The computation results fitted well with the test results. Different initial yaw angle had little effect on the pitching / yaw cycle of M852 bullet, but the larger the initial yaw angle was, the larger the motion amplitude, and the larger the lateral deviation, the faster the speed decreased. For Basic Finner model with low-speed rotation, the flight characteristics of different emission velocities were different, and it was embodied in the aspect of velocity evolution, displacement fluctuation and cone amplitude, etc..
spinning projectile;virtual flight;six degrees of freedom;M852;Basic Finner
2016-06-20
梁益铭(1991-),男,湖南会同人,助理工程师,硕士,研究方向:气动力以及飞行动力学控制。
V211.3
A
