基于目标双参数的末敏弹扫描角自适应调整

韩广超,王 锋,赵河明,彭志凌,刘建勋

(中北大学机电工程学院,太原 030051)

基于目标双参数的末敏弹扫描角自适应调整

韩广超,王 锋,赵河明,彭志凌,刘建勋

(中北大学机电工程学院,太原 030051)

针对末敏弹稳态扫描参数恒定,扫描规律一定,对不同参数目标,可能导致漏扫甚至无法及时发现目标的问题,提出了一种基于目标速度与长度的扫描角自适应调整方法。建立了末敏子弹扫描目标的关系模型,通过MATLAB进行了初始扫描角以及稳态扫描扫描角的确定。仿真结果表明:文中提出的扫描自适应调整方法,能快速调整扫描角,提高了扫描效率,便于及时发现目标,对末敏弹设计提供了一定的理论支持和数据参考。

末敏弹;扫描角;自适应调整;MATLAB

0 引言

末敏弹具有大面积封锁与杀伤性、效费比高以及打了不用管等优点[1],在现代战争中,针对装甲集群目标精确打击发挥了极其重要的作用。

从弹道运动角度来看,稳态扫描参数对子弹药系统性能与可靠性高低起着决定性作用,文献[2]研究了末敏弹稳态扫描的物理规律;文献[3-4]对末敏弹扫描角进行了研究;文献[5-6]对末敏弹稳态扫描特性进行了详细介绍,但是以上研究均属于传统稳态扫描方式,这种方式缺点就是扫描效率低,如果目标处于扫描中心,需长时间才能探测到目标甚至可能因子弹滞空时间长而被击落。从目标运动角度来看,影响末敏弹扫描效率主要是目标的速度和长度两种因素,文献[7-8]针对速度和长度两种因素就末敏弹的扫描运动只进行了简单叙述与介绍,没有深入研究。

未来装甲坦克为提高机动性,实现快速部署以及提高战场生存力,将会向高速、小型化方向发展[9-10],因此提高末敏弹的扫描效率,改善作战效能,是研究新一代末敏弹的主要任务之一,根据导弹导引头扫描技术原理[11-14],提出了基于目标速度与长度双参数的末敏弹扫描角自适应调整方法。

1 末敏子弹稳态扫描工作原理

末敏弹经火炮发射后,飞行到指定区域上空,母弹开舱抛射子弹体,减速减旋稳定后进入稳态扫描阶段,子弹体稳态扫描工作原理如图1所示。

稳态扫描过程:子弹轴与铅垂方向成某一角度值θ的子弹在摩擦盘导旋作用下,主旋转伞带动子弹同步旋转,与此同时,位于子弹上的敏感视场在地面以螺旋线的形式由外向内开始对目标进行搜索、探测、识别,一旦识别目标,即刻形成爆炸成型弹丸(explosively formed projectile,EFP),从顶部攻击装甲集群目标。

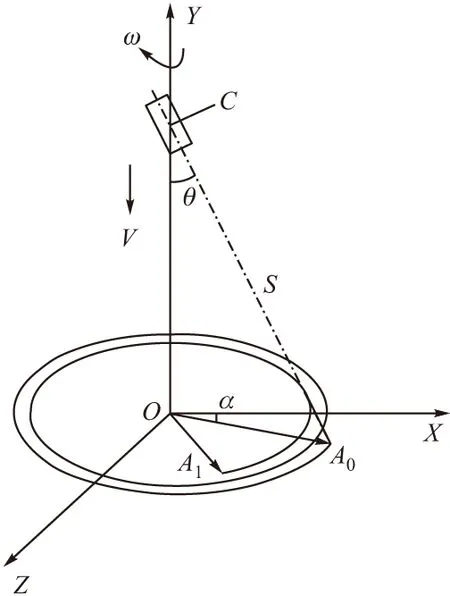
图1 末敏子弹稳态扫描原理图

假设子弹稳态扫描的初始高度为H,在螺线上的初始扫描位置为A0,初始位置与X轴成α,经时间t后为扫描螺线上的A1点,其坐标表示为:

(1)

由式(1)可得出扫描轨迹的极坐标:

r(t)=(H-vt)tanθexp(i(α+wt))

(2)

根据式(2)可知两相邻扫描螺线的距离为:

Δ=vtanθ/n

(3)

n=w/2π是子弹绕铅垂轴的角速度(r/s)。

2 末敏子弹扫描角自适应调整

2.1 末敏子弹扫描目标关系模型的分析与建立

根据文献[15]中研究识别方式对捕获准则的影响可知:在摆幅不大的情况下,“一次扫描”方式命中概率较高,因此,假设捕获准则为一次扫描,同时假设子弹在进行稳态扫描时目标处于扫描区域内部靠近中心处,目标如果要被扫描轨迹所覆盖,必须满足子弹在一个扫描周期内,目标向前行驶的距离为坦克标准长度减去N个扫描螺距,其中N≥1,目标运动与扫描轨迹关系如图2、图3、图4所示。

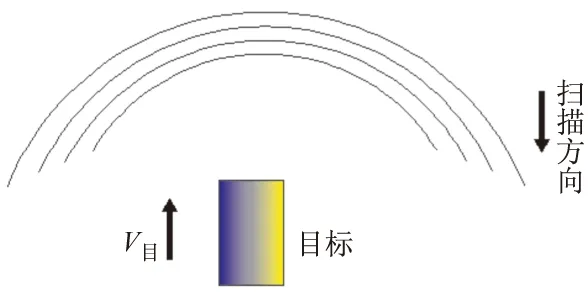
图2 目标未接触扫描轨迹线

因此用末敏弹攻击目标的理论速度值为:

(4)

式中N≥1且为整数值,L为坦克的标准长度。

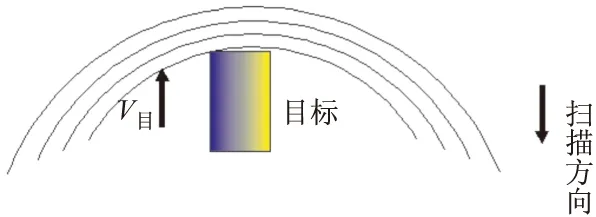
图3 目标开始接触扫描轨迹线

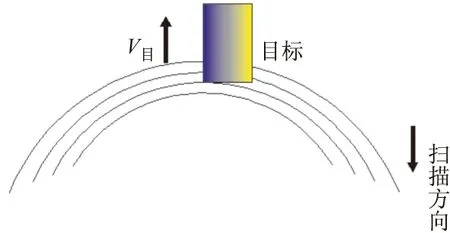
图4 目标穿过扫描轨迹线

战场上,如果目标速度与根据式(4)计算的理论值满足前者小于等于后者的话,可以用末敏弹进行攻击[16],但未来坦克如果满足前者大于后者的话,传统末敏弹将失去作用,为解决这方面的问题根据式(3)和式(4)从稳态扫描参数考虑,转速和落速均与主旋转伞有关,主旋转伞一旦设计好,转速和落速也就确定了[17],因此应从扫描角考虑,满足的关系式如下:

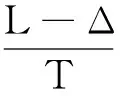
(5)

式(5)为子弹体扫描目标运动模型,如果目标标准长度减小,则理论速度减小,在目标速度增大的同时,若增大理论速度值,可减小扫描角,直到计算的理论速度值大于等于目标的速度为止。

2.2 末敏子弹扫描角自适应调整原理分析

根据式(5),如果目标速度大于理论速度时,通过降低扫描角来增大理论速度,所以扫描角自适应调整原理为:每完成一次扫描周期,扫描角θ变化一个Δθ,使得相邻两个扫描周期探测区域相切,可以避免探测区域重合,提高扫描效率。其自适应调整原理如图5所示。

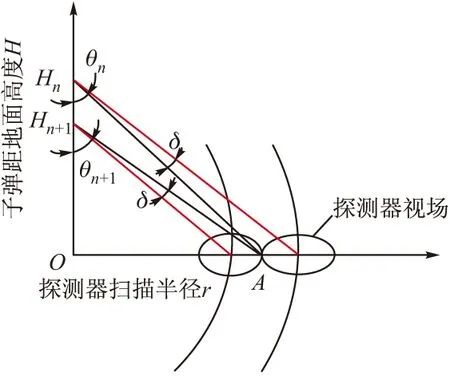
图5 扫描角自适应调整原理

Hn为当前时刻子弹距地面的高度,Hn+1为下一时刻子弹距地面的高度,两者之间时间差为一个扫描周期,A点为两次扫描探测区域相切点,则有:

Hntan(θn-δ)=Hn+1tan(θn+1+δ)

(6)

(7)

式中δ为红外敏感器的视场角,图6为扫描角自适应调整扫描原理图。

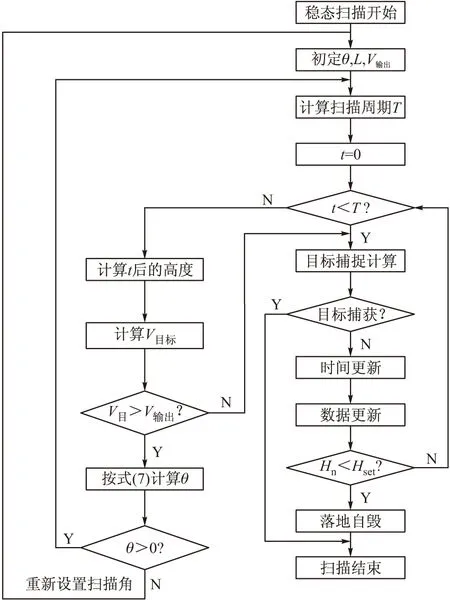
图6 末敏子弹扫描角自适应调整原理

2.3 扫描角自适应调整在工程中的实际应用

在2.2节描述的扫描角自适应调整原理中:两扫描区域相切,避免探测区域重合,在工程实际应用中,为保证目标不被探测器所漏扫,要求探测区域出现一定的重合,因此在实际应用中,需引入扫描角补偿系数ε,其作用就是对扫描角进行修正,从而保证探测区域达到一定重合度,同时在设计静态悬挂角时,扫描角必须设置最低门限值γ和最高门限值β,这样才能保证有一定的扫描区域,并且保证子弹体系统的稳定性。修正后的扫描角如下:

(8)

根据式(7)和式(8)得出的扫描角就可满足工程中实际应用。

3 扫描角自适应调整仿真分析

初始参数设定:子弹药稳态扫描时距地面高度H=600 m,转速n=4 r/s,落速v=14 m/s,红外敏感器视场角δ=1.6°目标标准长度L=6 m,目标实际速度定为82.8 km/h,根据式(4)、式(5)、式(7)三式,初步选定初始扫描角即静悬挂角的范围为5°～39°。

3.1 初始扫描角和稳态扫描角的确定

根据末敏子弹扫描角自适应调整原理,编写仿真代码,仿真得出各初始扫描角下,经自适应调整后达到的稳态扫描角以及所用的时间如表1所示。

表1 初始扫描角与稳态扫描角及时间关系

从表中数据可以看出:

1)时间均为扫描周期的整数倍;

2)扫描角每3°变化,其时间是相同的,最终达到稳态扫描角的范围基本在1°～4°之间且变化平稳,只有在初始扫描角为29°～32°时,每4°变化。

扫描角选取原则:既保证时间短,又保证扫描角最大,综合表中数据,将初始扫描角定在7°,确定的稳态扫描角为3.831 7°,此时时间最短为一个扫描周期,稳态扫描角较大,满足扫描角选取原则。

3.2 扫描轨迹分析

在同一稳态扫描开始高度,同一落速,同一转速下,传统末敏弹(扫描角为30°)的扫描轨迹和扫描角自适应调整后的扫描轨迹分别如图7和图8所示。

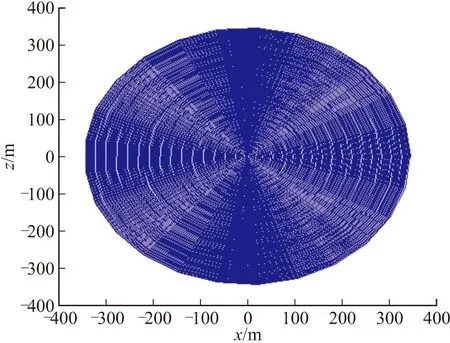
图7 传统扫描角为30°时的扫描轨迹

图8 扫描角自适应调整后的轨迹

传统扫描角为30°时,目标实际速度要远大于所计算的理论值,此时不能用末敏弹攻击目标。为满足目标实际速度小于等于理论速度,经扫描角自适应调整后,扫描角变得很小,在稳态扫描开始高度相同的情况下,探测器扫描范围会明显降低,同时扫描间隔也会大幅减小,这样会使得目标被扫描到的几率增加,提高子母弹的作战效能。

4 结论

文中针对目标长度与速度两参数,在目标速度大于理论目标速度时,传统子母弹扫描效率下降,提出了基于目标双参数的末敏弹稳态扫描角自适应调整方法。通过仿真分析:该方法能够快速调整扫描角,不仅提高扫描效率,而且能够及时发现目标。通过分析得出以下几点结论:

1)根据子弹与目标运动模型可知:扫描角自适应调整中,扫描角逐渐减小,所以从扫描轨迹看方向由外向内,在目标速度较大,标准长度减小的情况下,目标应位于子母弹的扫描轨迹内,因此,在火炮发射末敏弹时,应调整射击诸元,使目标处于扫描轨迹内。

2)文中提出的扫描角自适应调整方法,对末敏弹的研究与设计提供了一定的技术和方法支持,具有一定的现实指导意义。

3)文中得出的结果存在一种缺陷:当目标的速度和长度确定时,经调整后的稳态扫描角很小,虽然扫描间隔减小了,增加了目标被扫描几率,但探测器的扫描范围却大大的降低了。

4)文中是在理想状态即无风影响下,对末敏弹扫描角进行的自适应调整研究,但在实际情况下,风的影响可能会对扫描角产生一定的影响,因此研究风作用下的末敏弹扫描角自适应调整对末敏弹的研究与设计更具有一定的现实与应用指导意义。

[1] 郑荣跃, 秦子增. 子母弹研究进展 [J]. 国防科技大学学报, 1996, 18(1): 60-64.

[2] 李臣明, 韩子鹏, 刘怡昕, 等. 基于四元数法变换的末敏弹扫描运动研究 [J]. 兵工学报, 2009, 30(4): 389-393.

[3] 马凯臣, 曹咏弘, 范锦彪. 基于公式近似的末敏弹扫描角计算方法 [J]. 探测与控制学报, 2011, 33(5): 52-55.

[4] 刘文举, 魏琳, 钟录宏. 末敏子弹稳态扫描角仿真模型研究 [J]. 弹箭与制导学报, 2010, 30(6): 108-109.

[5] 顾建平, 韩子鹏. 末敏弹扫描运动的影响因素分析 [J]. 弹箭与制导学报, 2009, 29(3): 136-138.

[6] 史金光, 韩子鹏, 舒敬荣, 等. 双翼型无伞末敏弹稳态扫描运动数学模型 [J]. 弹道学报, 2010, 22(2): 24-27.

[7] 赵新生, 邢立新, 孙超. 末敏弹稳态扫描段扫描间隔分析 [J]. 弹箭与制导学报, 2005, 25(4): 900-902.

[8] 程杰, 张凌海. 末敏弹稳态扫描段扫描间隔对射击效果的影响分析 [J]. 电脑知识与技术, 2014, 10(20): 4857-4859.

[9] 袁常卿, 苏铁熊. 未来坦克装甲车辆技术的发展趋势 [J]. 机械管理开发, 2007(1): 11-12.

[10] 郭正祥. 用对比分析法评判坦克优劣——世界坦克排行榜值得商榷 [J]. 国外坦克, 2012(10): 13-17.

[11] 吴文超, 黄长强, 王志军, 等. 某型导弹导引头定向扫描技术 [J]. 空军工程大学学报(自然科学版), 2010, 11(3): 30-34.

[12] CARLSON B D, EVANS E D, WILSON S L. Search radar detection and track with the hough transform: Part Ⅰ System concept [J]. IEEE Transactions on Aerospace and Electronic Systems, 1994, 30(1): 102-108.

[13] CARLSON B D, EVANS E D, WILSON S L. Search radar detection and track with the hough transform: Part Ⅱ Detection statistics [J]. IEEE Transactions on Aerospace and Electronic Systems, 1994, 30(1): 109-115.

[14] CARLSON B D, EVANS E D, WILSON S L. Search radar detection and track with the hough transform: Part Ⅲ Detection performance with binary integration [J]. IEEE Transactions on Aerospace and Electronic Systems, 1994, 30(1): 116-125.

[15] 杨绍卿. 末敏弹系统理论 [M]. 西安: 陕西科学技术出版社, 2009: 54-67.

[16] 翟保磊, 李波, 高晓光. 基于扫描角控制的末敏弹稳态扫描方法 [J]. 电光与控制, 2013, 20(6): 58-61.

[17] 杨绍卿. 灵巧弹药工程 [M]. 北京: 国防工业出版社, 2010: 149-157.

Self-adaptive Adjustment of the Scanning Angle of Terminal-sensitivity Projectile Based on Target Double Parameters

HAN Guangchao,WANG Feng,ZHAO Heming,PENG Zhiling,LIU Jianxun

(School of Mechatronics Engineering, North University of China, Taiyuan 030051, China)

For terminal-sensitivity projectile(TSP)steady state scanning parameters were constant, and the law of scanning was certain, for the target with different parameters, it might lead to leakage scanning, and it even could not find the problem of the target in time, a method of the scanning angle self-adaptive adjustment of TSP based on target speed and length was proposed. The relation model of TSP and target was established, and then, the initial scanning angle as well as the steady state scanning angle was confirmed by MATLAB. The simulation results showed that: the method of self-adaptive adjustment presented in this paper could quickly adjust the scanning angle, and it improved scanning efficiency, and help it find the target in time. What’s more, the theoretical support and data reference were provided for the design of the TSP.

terminal-sensitivity projectile(TSP); scanning angle; self-adaptive adjustment; MATLAB

2016-01-22

国防科工局技术基础项目资助

韩广超(1989-),男,山东济宁人,硕士研究生,研究方向:智能弹药、探测制导与控制。

TJ410.1

A