基于IMM-CKF的弹道再入目标跟踪研究

许登荣,程水英,包守亮

(电子工程学院,合肥 230037)

基于IMM-CKF的弹道再入目标跟踪研究

许登荣,程水英,包守亮

(电子工程学院,合肥 230037)

该文研究了弹道系数未知的弹道再入目标的跟踪问题。针对现有再入目标跟踪方法对弹道系数初值设定以及噪声协方差的设置比较敏感的问题,采用了数值精度高、稳定性好且计算量较小的求容积卡尔曼滤波(CKF)算法作为跟踪滤波器,并分别设计了由不同弹道系数模型构成的交互式多模型(IMM)算法以及由不同噪声协方差模型组成的IMM算法。仿真结果表明,该文设计的两种IMM算法都能显著提高跟踪精度以及对弹道系数估计的收敛速度。

弹道再入目标跟踪;交互式多模型算法;求容积卡尔曼滤波;弹道系数

0 引言

对弹道式再入目标的跟踪与识别是攻防对抗体系中的关键环节,有效精确的跟踪不仅可以延长防御方的反应时间而且可以提高拦截的准确度[1]。其跟踪的难点在于目标的弹道系数未知,需要对弹道系数进行实时估计,而对弹道系数估计的准确性影响着目标运动模型的准确性,进而决定了估计的精度。通常的做法是将弹道系数扩展为状态向量的一个分量进行联合[2-3],但是该方法对弹道系数初值的设置以及过程噪声协方差矩阵的设定都比较敏感。若先验信息不准确或上述参数设置不合理都会导致滤波器的估计精度下降,甚至会造成滤波器发散。因此,设计鲁棒性强、精度高且稳定性好的跟踪算法是解决该问题的关键。

此外,再入弹道目标的状态方程和雷达的量测方程通常都是非线性的,再入目标跟踪是一个典型的非线性滤波问题,比较各种非线性滤波方法在弹道再入目标跟踪中的性能一直以来是一个研究热点问题[4]。典型的非线性滤波方法有:扩展卡尔曼滤波(EKF)、无味卡尔曼滤波(UKF)[5-6]、粒子滤波(PF)[7]以及它们的改进算法等。EKF在系统非线性较强时,估计偏差较大,容易造成滤波器发散,同时需要计算Jacobian矩阵,当系统不连续可微分时自然失效。UKF的滤波精度和适用范围要优于EKF,但是对于高维的非线性系统,UKF需要合理的选择参数才能取得较好的滤波效果,对参数的选择具有一定的依赖性[5]。而PF滤波计算量过大,难以满足弹道再入目标跟踪的实时性要求。近年来,Arasaratmam和Haykin[8]提出的一种新的非线性滤波器——求容积卡尔曼滤波器(CKF),CKF采用3阶球面-相径容积规则来近似经非线性系统分布函数传递的后验均值和协方差。与EKF相比,它避免了对非线性系统线性化的要求;而与UKF相比,CKF的容积点和权值由状态向量的维数唯一确定,算法设计和实现更为简单。同时计算量较小,因此,CKF一经提出,就得到了广泛的应用[9-10]。

综合算法各方面的性能,该文采用CKF作为弹道再入目标的跟踪滤波器。同时为了解决弹道系数未知时弹道再入目标跟踪的问题,文中采用IMM算法与CKF算法相结合的方法,在仿真分析的基础上,设计了适用于弹道再入目标跟踪的IMM算法的模型集。仿真结果表明,在弹道系数未知时,采用文中设计的IMM算法能实现对弹道再入目标更高精度的跟踪,同时算法的稳定性和鲁棒性也得到了提高。

1 弹道再入目标的运动方程及量测方程

1.1 弹道再入目标运动方程

弹道再入目标重返大气时,受到的作用力主要有地球重力和空气动力。对于非机动再入目标,空气动力表现为大气阻力,其方向与目标速度的方向相反。假设地球是一个标准的球体,并忽略地球的旋转。设p=[xyz]T为目标在雷达站东北天(ENU)坐标系中的位置矢量,v=[vxvyvz]T为目标在ENU坐标系中的速度矢量,则目标在ENU坐标系中的运动方程为:

(1)

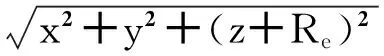
(2)

式(2)按Euler逼近法离散化得:

xk+1=xk+Tf1(xk)+wk=f(xk)+wk

(3)

式中:T表示采样间隔;wk为离散时间的过程噪声,其协方差矩阵为:

(4)

式中:⊗为Kronerker积,I3为3×3的单位矩阵;q是目标加速度过程噪声的方差;qα表示阻力参数的过程噪声方差。

1.2 量测方程

反导雷达的量测在球坐标中获得,量测方程为:

(5)

式中:xk、yk、zk是目标k时刻在雷达ENU坐标系下的位置坐标;zk=[R,A,E]T是k时刻雷达的观测值,其中R为目标到雷达的距离,A为方位角,E为俯仰角;vk是零均值的高斯白噪声序列,其协方差矩阵为Rk。

2 求容积卡尔曼滤波算法

将式(3)和式(5)的状态方程和量测方程重写如下:

(6)

式中:xk∈Rnx、zk∈Rnz,nx=7为状态向量的维数,nz=3为状态向量的维数。f(·)、h(·)为非线性函数。

弹道再入目标跟踪实际上是对上述离散的非线性系统的递推估计问题。由于式(6)所表示系统的非线性较强,且综合考虑工程应用和滤波器的性能,文中采用CKF作为跟踪滤波器,现将其算法步骤总结如下。

2.1 初始化

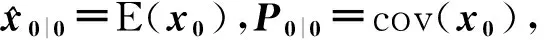
(7)

式中:m=2nx,记nx维单位向量为e=[1,0,…,0]T,符号[1]表示对e中元素进行全排列和取反所生成的点集,即:

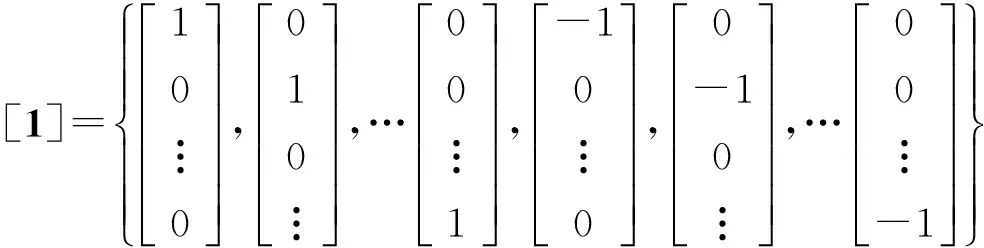
(8)

该点集称为完整全对称点集,[1]i表示点集中的第i个点。

2.2 时间更新

1)对k-1时刻的状态协方差矩阵Pk-1|k-1进行Cholesky分解,即:

(9)

2)计算状态求容积点

(10)

3)计算经非线性函数传播后的求容积点

(11)

4)状态的一步预测

(12)

5)状态协方差的一步预测

(13)

2.3 量测更新

1)矩阵分解

(14)

2)计算量测求容积点

(15)

3)计算传播后的求容积点

Zi,k|k-1=h(Xi,k|k-1)

(16)

4)量测的一步预测

(17)

5)计算新息协方差

(18)

6)计算互协方差

(19)

7)计算增益

(20)

8)状态更新

(21)

9)协方差更新

(22)

3 IMM-CKF算法设计

对弹道再入目标跟踪的难点在于难以对目标运动进行准确的建模,对于防御方而言,目标的弹道系数通常是未知的,或只能知道其所在大致的区间,因而需要对其进行估计,而在估计收敛之前,目标的运动模型是不准确的。在系统状态方程不确定或含有未知参数时,采用多模型估计方法通常能取得比较好的性能。在所有的多模型估计方法中,IMM算法通过合理的假设,一般被认为是一种最有效的混合估计方案,并得到了广泛的应用。文中采用IMM算法实现对再入目标的跟踪,首先根据弹道系数大致分布的范围,构造了由3个不同弹道系数初值{βi,(i=1,2,3)}滤波器作为模型集的IMM算法。另外考虑到过程噪声协方差的设置同样会影响弹道系数估计的收敛速度,文中也同时设计了由3个不同过程噪声协方差{qα,i,(i=1,2,3)}滤波器组成的IMM算法。在滤波过程中,IMM算法通过各模型之间进行交互的同时更新各模型的模型概率来实现对未知参数更迅速的估计,从而获得更高的滤波精度。

IMM估计算法的步骤如下。

步骤1 模型条件重初始化

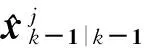
(23)

(24)

其中:

(25)

步骤2 模型条件滤波

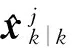
步骤3 模型概率更新

(26)

式中:

(27)

步骤4 估计融合

(28)

(29)

4 仿真分析

设计一条标准的再入弹道轨迹,目标的再入速度为3 000 m/s,再入角为39°,初始时刻目标在雷达ENU坐标系的位置为(130 km,50 km,95 km),目标的弹道系数为常值5 000 kg/m2。采用四阶龙格库塔积分法外推生成标准弹道,图1为目标在雷达ENU坐标系中的弹道曲线,图2、图3分别是再入目标的加速度和速度变化曲线。假设雷达跟踪数据率为10 Hz,雷达的测距精度为σR=50 m,测角精度σA=σE=1 mrad,且量测噪声服从高斯分布,整个跟踪过程中雷达的测距和测角精度保持不变。

图1 目标的弹道曲线

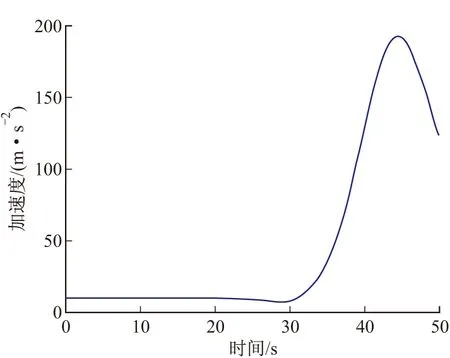
图2 目标的加速度变化曲线

图3 目标的速度变化曲线

首先分析不同弹道系数初值对跟踪精度以及收敛速度的影响。结合弹道再入目标弹道系数可能的范围,设计了如下3个CKF滤波器和IMM估计器:

求容积卡尔曼滤波器1(CKF1):导弹系数初值为3 000 kg/m2,过程噪声协方差矩阵的q=0.1 m2·s-4,qα=10-12。

求容积卡尔曼滤波器2(CKF2):导弹系数初值为6 000 kg/m2,过程噪声协方差矩阵的q=0.1 m2·s-4,qα=10-12。

求容积卡尔曼滤波器3(CKF3):导弹系数初值为9 000 kg/m2,过程噪声协方差矩阵的q=0.1 m2·s-4,qα=10-12。

采用上述3个不同弹道系数初值的CKF算法以及由上述3个滤波器作为模型集的IMM算法(IMM1算法)分别对目标进行跟踪。IMM算法的模型初始概率及概率转移矩阵分别为:

采用两点初始化的方法,Monte Carlo仿真实验50次。图4～图6分别给出了各算法的位置、速度以及弹道系数估计的均方根误差曲线。

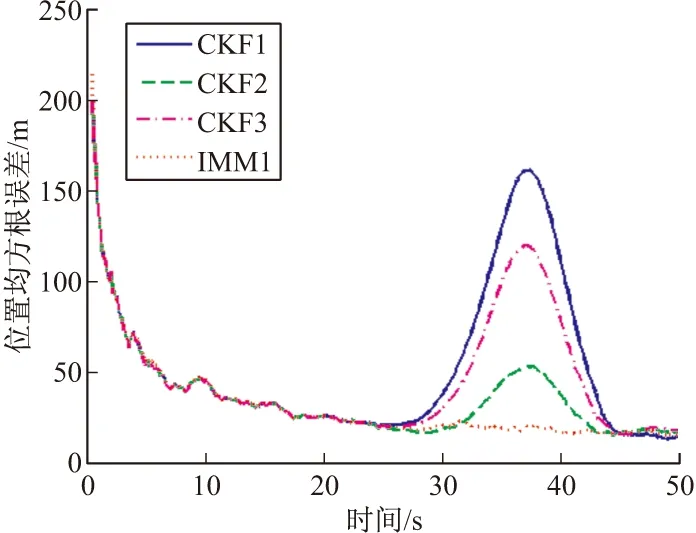
图4 位置均方根误差

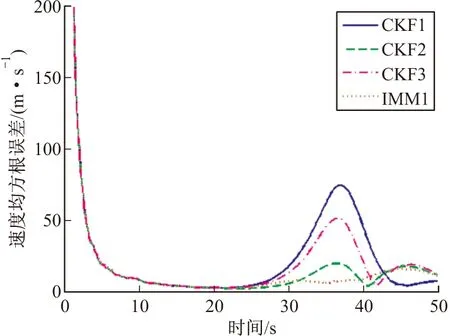
图5 速度均方根误差

仿真结果表明,总体来说,滤波器的弹道系数初值离真值越远,跟踪效果越差,尤其是当目标空气阻力加速度增大时,弹道系数初值离真值较远的CKF算法估计误差会明显增大。而采用IMM算法可以有效的降低估计误差,提高跟踪的精度,表明降低了算法对弹道系数初值设置的敏感性,提高了算法的鲁棒性。而从图6可以看到,IMM算法对导弹系数估计的收敛速度最快,导致运动模型更加的准确,从而滤波精度最高。同时也不难发现,弹道系数估计收敛速度越快的算法跟踪误差越小。

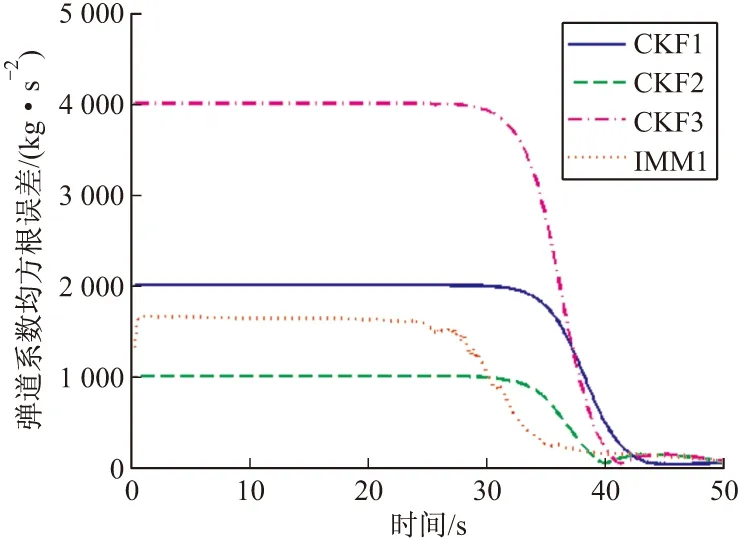
图6 弹道系数均方根误差

接下来分析滤波器设置不同过程噪声协方差对跟踪精度以及收敛速度的影响。设计了如下3个CKF滤波器和IMM算法:

求容积卡尔曼滤波器4、5、6(即CKF4、CKF5、CKF6)的导弹系数初值均为3 000 kg/m2,过程噪声协方差矩阵的q均为0.1 m2·s-4,qα分别为10-8、10-11、10-12。采用上述3个不同过程噪声协方差的CKF算法以及由上述3个滤波器作为模型集的IMM算法(IMM2算法)分别对目标进行跟踪。并根据再入目标运动的特点,IMM算法的模型初始概率及概率转移矩阵设置为:

同样采用两点初始化的方法,Monte Carlo仿真实验50次。图7～图9分别给出了各算法的位置、速度以及弹道系数估计的均方根误差曲线。

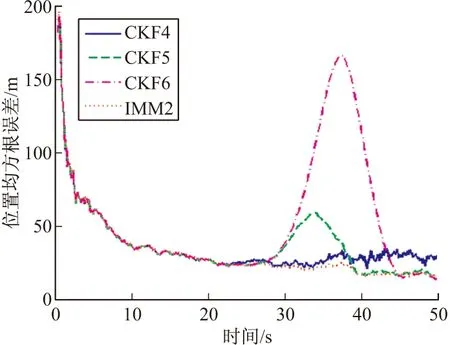
图7 位置均方根误差

图8 速度均方根误差

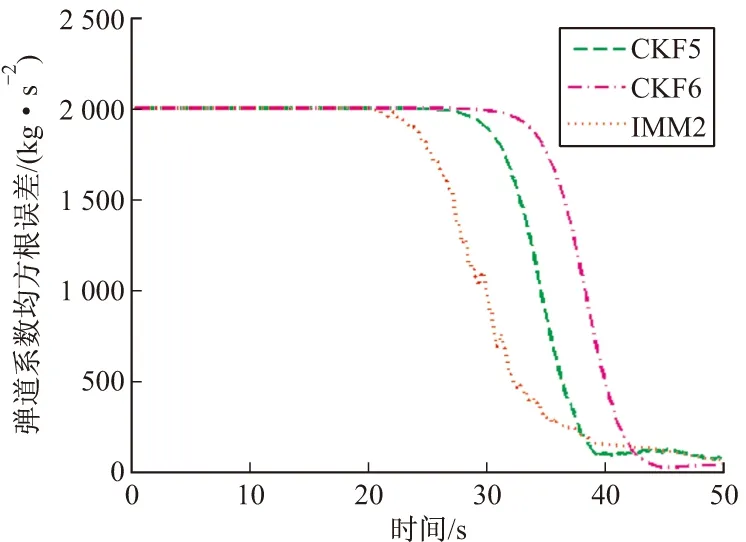
图9 弹道系数均方根误差

过程噪声表征模型的不确定性程度,过程噪声越大,不确定程度越高,调节作用越大,过程噪声越小,模型不确定程度越低,调节作用也越小。仿真结果表明,若qα设置在合理范围内,qα设置越大,对弹道系数估计的收敛速度也就越快。CKF4由于qα设置过大,导致对弹道系数估计的不确定性较大,几乎不能估计出导弹系数的大小,因而在未在图9中画出弹道系数的均方根误差曲线,且其位置和速度滤波的精度也不太高,波动较大。而CKF6算法和CKF5算法由于qα设置较小,虽然最后对弹道系数的估计比较精确,但是由于调节作用小,导致滤波器的收敛速度慢,因而当空气阻力增大时,位置估计和速度估计都出现较大的偏差。目标再入时,刚开始空气阻力较小,但会慢慢增大,不确定程度高,因而qα应该设置一个较大的值;当对弹道系数的估计越来越准确时,qα应该设置一个较小的值,以提高对弹道系数估计的准确性。文中就是根据上述思想设计IMM2算法,可以看到,相对其他算法,IMM算法的跟踪精度有了很大的提高,对弹道系数估计的收敛速度明显增快。改变滤波器弹道系数的初值,仿真发现,采用这种由不同过程噪声协方差滤波器组成的IMM算法同样有着很强的调节能力,对滤波器弹道系数初值设定的敏感程度低。

文中也对滤波器过程噪声协方差设置不同的q值对跟踪精度的影响进行了分析,仿真发现,对非机动再入,只要对q设置一个较小的值,就能保准跟踪的精度和收敛速度,滤波器对该参数不太敏感。但考虑到实际跟踪中可能会受到一些随机扰动的影响,IMM算法应该考虑采用不同弹道系数初值、不同过程噪声协方差矩阵(同时考虑q和qα)的滤波器的组合作为IMM算法的模型集,在保准跟踪精度的同时进一步提高算法的鲁棒性。

5 结论

针对弹道系数未知的弹道目标的跟踪问题,在仿真分析的基础上,设计了由不同弹道系数初值模型构成的IMM算法以及由不同阻力参数噪声方差模型组成的IMM算法,仿真结果表明,两种IMM算法都能有效减轻算法对弹道系数初值设定的敏感性,跟踪精度以及对弹道系数估计的收敛速度都得到了显著的提高。

[1] 张龙, 崔乃刚, 王小刚, 等. 强跟踪-容积卡尔曼滤波在弹道式再入目标跟踪中的应用 [J]. 中国惯性技术学报, 2015, 23(2): 211-218.

[2] CARDILLO G P, MRSTIK A V, PLAMBECK T. A track filter for reentry objects with uncertain drag [J]. IEEE Transactions on Aerospace and Electronic Systems, 1999, 35(2): 394-409.

[3] LI X R, JILKOV V P. Survey of maneuvering target tracking. Part II: Motion models of ballistic and space targets [J]. IEEE Transactions on Aerospace and Electronic Systems, 2010, 46(1): 96-119.

[4] SINGH N K, BHAUMIK S, BHATTACHARYA S. A comparison of several nonlinear filters for ballistic missile tracking on re-entry [C]∥2016 IEEE First International Conference on Control, Measurement and Instrumentation (CMI), 2016: 459-463.

[5] JULIER S J, UHLMANN J K. Unscented filtering and nonlinear estimation [C]// Proceedings of the IEEE, 2004, 92(3): 401-422.

[6] 程水英. 无味变换与无味卡尔曼滤波 [J]. 计算机工程与应用, 2008, 44(24): 25-35.

[7] 程水英, 张剑云. 粒子滤波评述 [J]. 宇航学报, 2008, 29(4): 1099-1111.

[8] ARASARATNAM I, HAYKIN S. Cubature Kalman filters [J]. IEEE Transactions on Automatic Control, 2009, 54(6): 1254-1269.

[9] CHEN Hai, SHAN Ganlin. Attitude angle aided IMMCKF algorithm [C]∥IEEE 2011 10th International Conference on Electronic Measurement & Instruments, 2011: 197-200.

[10] 孙钰琛, 段凤阳, 李赞平. 基于平方根容积卡尔曼滤波的SINS大失准角快速对准方法 [J]. 弹箭与制导学报, 2014, 34(4): 25-28.

[11] BAR-SHALOM Y, LI X R, KIRUBARAJAN T. Estimation with applications to tracking and navigation: theory, algorithms and software [M]. [S.l.]:John Wiley & Sons Inc., 2001.

Research on Ballistic Reentry Target Tracking Based on IMM-CKF

XU Dengrong,CHENG Shuiying,BAO Shouliang

(Electronic and Engineering Institute, Hefei 230037, China)

The tracking of ballistic reentry target with unknown ballistic coefficient was studied in this paper. In view of the problems that the existing reentry target tracking method was both sensitive to the ballistic coefficient initialization and the noise covariance setting, the cubature kalman filter (CKF) algorithm which has high numerical accuracy, good stability and small computation quantity was adopted as filtering, then the IMM algorithms composed of models with different ballistic coefficient and different noise covariance were designed respectively. Computer simulation results showed that the two IMM algorithms designed in this paper could significantly improve the tracking accuracy and the convergence rate of the ballistic coefficient estimation.

ballistic reentry target tracking; interactive multiple model algorithm; cubature Kalman filter; ballistic coefficient

2016-04-20

许登荣(1991-),男,湖南邵阳人,硕士研究生,研究方向:雷达数据处理。

TN95

A