树Tn与路Pm的笛卡尔积图的交叉数
2017-06-22胡宁贝魏首柳白银燕
胡宁贝,魏首柳,白银燕
(闽江学院 数学系,福建 福州 350121)
树Tn与路Pm的笛卡尔积图的交叉数
胡宁贝,魏首柳,白银燕
(闽江学院 数学系,福建 福州 350121)
图的交叉数是图论中一个重要的研究课题.分别记含有n+1个顶点的树和路为Tn与Pn,通过数学归纳法验证并计算得到了笛卡尔积图Tn×Pm的交叉数,其中n≤4.
笛卡尔积图;好画法;交叉数;树;路
令G表示一个简单连通图.设V(G)和E(G)分别表示图G的顶点集和边集.G1×G2表示图G1和G2的笛卡尔积图,具体定义如下:V(G1×G2)=V(G1)×V(G2),E(G1×G2)={(u1,u2)(v1,v2)|u1=v1且u2v2E(G2)或者u2=v2且u1v1E(G1)}.图的交叉数问题是近代图论中一个重要的研究课题.图G的交叉数[1]指图G在平面上所有好画法中边与边之间相互交叉的最小顶点数,用cr(G)表示.其中,好画法满足:①相互交叉的任何两条边最多仅在顶点处交叉;②边不能自身相交;③有相同端点的两条边不交叉;④任何3条边都不可能交叉于同一顶点.最优画法指含最小交叉数的好画法,用crD(G)表示图G在好画法时D的交叉数.如果没有特别说明,本研究涉及的一些概念和术语均来自文献[2].
图的交叉数的确定问题不仅在理论研究中具有非常重要的意义,而且在诸多实际问题中也有相应的研究背景,如超大规模集成电路VLSL中圈的布局[3-5]、离散几何与计算几何的研究及软件开发过程中文档的实体联系图(ER图)的自动生成和工业上电子线路板设计中的布线问题等.
国内外学者对图的交叉数的计算问题已经做了大量的分析和研究,也得到了一些成果.1993年,Garey和Johnson[6]研究并证明了图的交叉数问题是一个NP-完全问题.但是,由于其研究方法不统一,导致能够被准确计算出交叉数的显式表达式的图类比较少,主要针对一些相对比较特殊的图类(特别是笛卡尔积图)的交叉数[7-12],而对于树与其他特殊图类的笛卡尔积图的交叉数的研究结果,目前集中在袁梓瀚[13]的博士论文和刘伟[14]的硕士论文中,柯小玲[15]也研究了不大于5个顶点的树与圈的笛卡尔积图的交叉数问题,本课题进一步研究不大于5个顶点的树与路的笛卡尔积图的结构并给出了其交叉数的显式表达式.
1 预备知识
Tn表示含有n+1个顶点的树;Sn表示含有n+1个顶点的星图,即完全图K1,n;Pn表示含有n+1个顶点的路; [x]表示不超过x的最大整数.
定义1 图G和H为同构的,如果存在两个一一映射θ∶V(G)→V(H)和φ∶E(G)→E(H),使得ΦG(e)=uv当且仅当ΦH(φ(e))=θ(u)θ(v),记为G≌H.
引理1 若H为图G的子图,则cr(H)≤cr(G).
引理2(Jordan曲线定理) 平面上的任一简单闭曲线将平面唯一地分成3个彼此不相交的点集J, int(J),ext(J),则
(1)int(J)是一个有界区域,称为J的内部;ext(J)是一个无界区域,称为J的外部.
(2)int(J)和ext(J)都以J为边界,如图1所示.
引理3 cr(Pn×Pm)=0.
证明 图2是Pn×Pm的一个好画法,记为D,所以Pn×Pm显然是平面图,故有cr(Pn×Pm)=0.
引理4 cr(S3×Pm)=m-1,m≥1.
引理5 cr(S4×Pm)=2(m-1),m≥1.
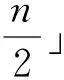
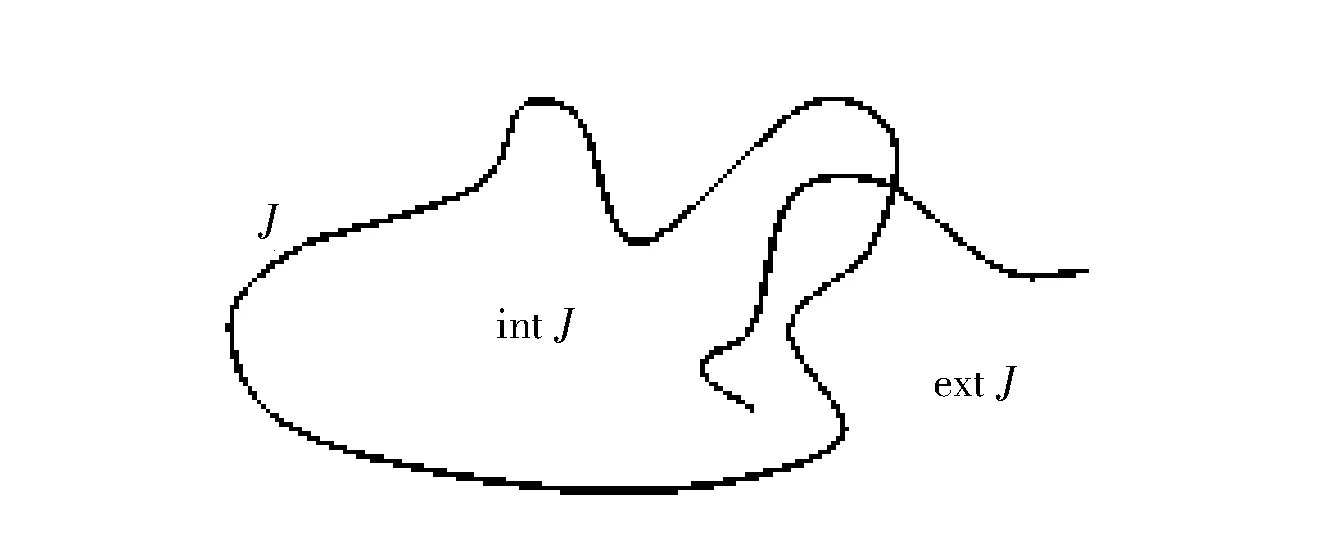
图1 Jordan曲线图Fig.1 Graph for Jordan curve

图2 Pn×Pm的一个好画法Fig.2 A good drawing of Pn×Pm
2 主要结果及其证明
众所周知,任何一棵树Tn(n≥3)在同构意义下均存在2个或2个以上的非同构图.下面,对含有不多于5个顶点的树Tn(n≤4)与路Pm的笛卡尔积图进行研究,得到它们的交叉数表达式.
令T1和T2分别表示2阶和3阶的两棵树(见图3),则树T1与路P1显然同构,树T2与路P2显然也同构,根据引理3可以得到以下两个结果:
定理1cr(T1×Pm)=0,m≥1;
定理2cr(T2×Pm)=0,m≥1.
显然,含有4个顶点的树T3在同构意义下存在2个非同构图,分别记为T31和T32(见图4).由于树T31和T32分别与路P3和星图S3同构,则根据引理3和引理4可以得到如下结果:
定理3cr(T31×Pm)=0,m≥1;
定理4cr(T32×Pm)=m-1,m≥1.
含有5个顶点的树T4的3个非同构图可用T41,T42,T43表示(见图5),则由于树T41与路P4同构,树T42与星图S4同构,所以根据引理3、引理5和引理6可得到如下结果:
定理5cr(T41×Pm)=0,m≥1;
定理6cr(T42×Pm)=2(m-1),m≥1.
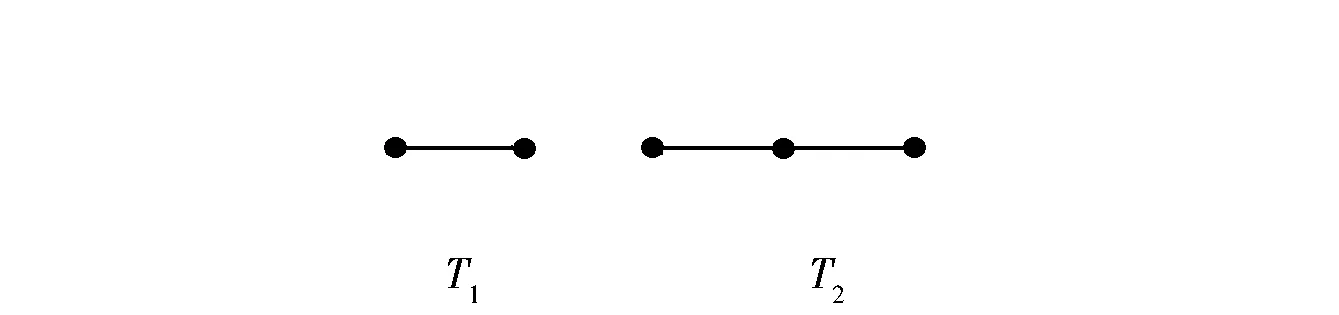
图3 2阶树T1与3阶树T2Fig.3 Trees with order 2 and 3
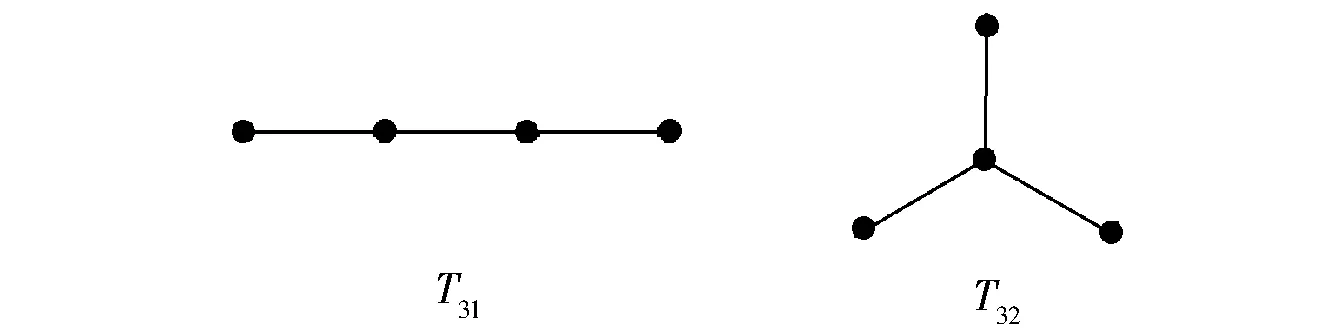
图4 4阶树的2个非同构图T31与T32Fig.4 Two non-isomorphic graphs of tree with order 4
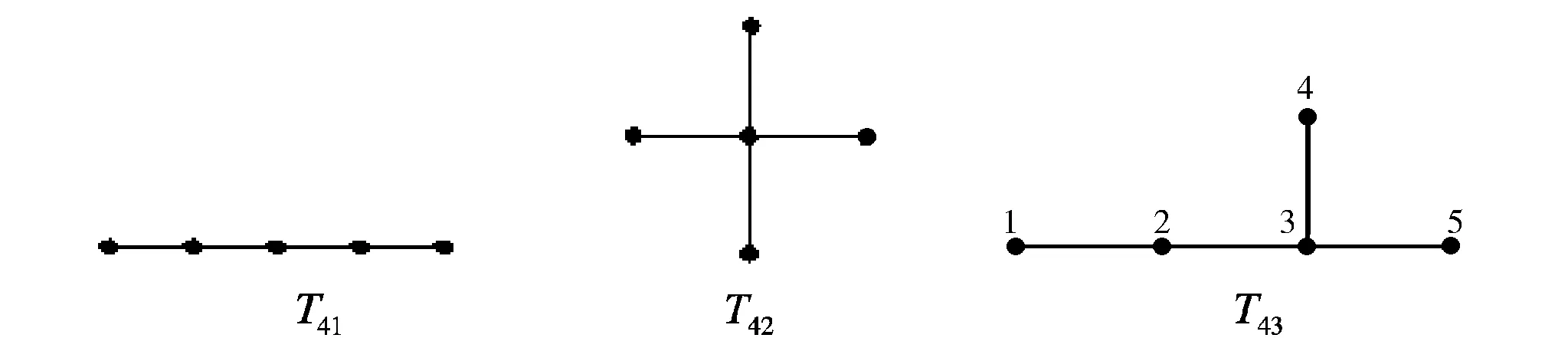
图5 5阶树的3个非同构图Fig.5 Three non-isomorphic graphs of tree with 5 order
用数学归纳法证明笛卡尔积图T43×Pm的交叉数.为了更好地研究和得到归纳基础,先证明以下几个重要结果.
引理7 cr(T43×P1)=0.
证明T43×P1是一个平面图(见图6),故有cr(T43×P1)=0.
引理8 cr(T43×P2)=1.
证明 因为图7是T43×P2的其中一个好画法,从而有cr(T43×P2)≤1.另一方面,如果能够证明cr(T43×P2)≥1,则结论成立.
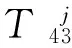
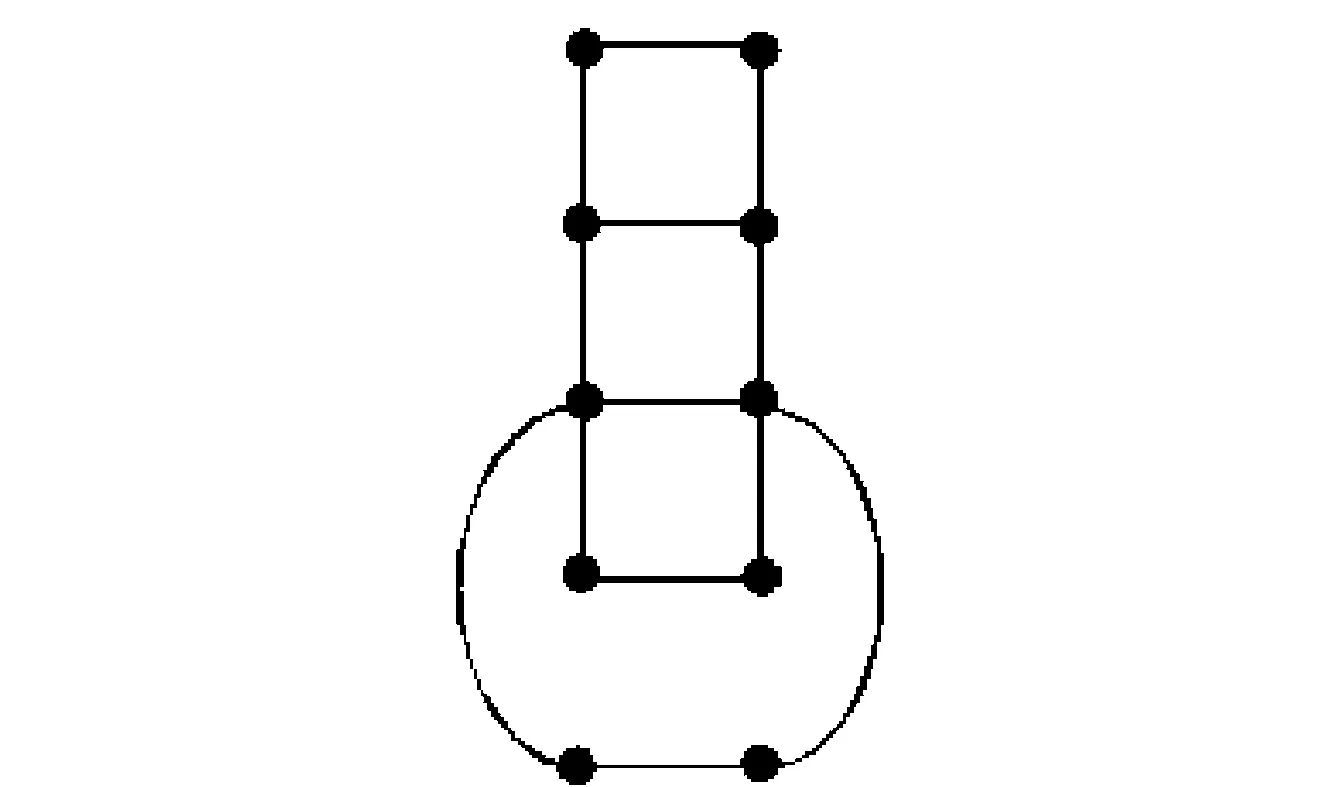
图6 T43×P1的一个好画法Fig.6 A good drawing of T43×P1
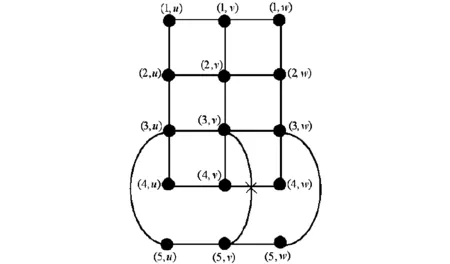
图7 T43×P2的一个好画法Fig.7 A good drawing of T43×P2
引理9 cr(T43×P3)=2.
证明 由T43×P3的一个好画法(见图8)可知,cr(T43×P3)≤2,只需要证明cr(T43×P3)≥2成立即可.选取笛卡尔积图T43×P3的一个子图H(见图9),根据引理1可得cr(T43×P3)≥cr(H).显然,T43×P3的子图H与S3×P3同构,又根据引理4可以得到cr(H)=cr(S3×P3)=2,所以cr(T43×P3)≥2,故有cr(T43×P3)=2.
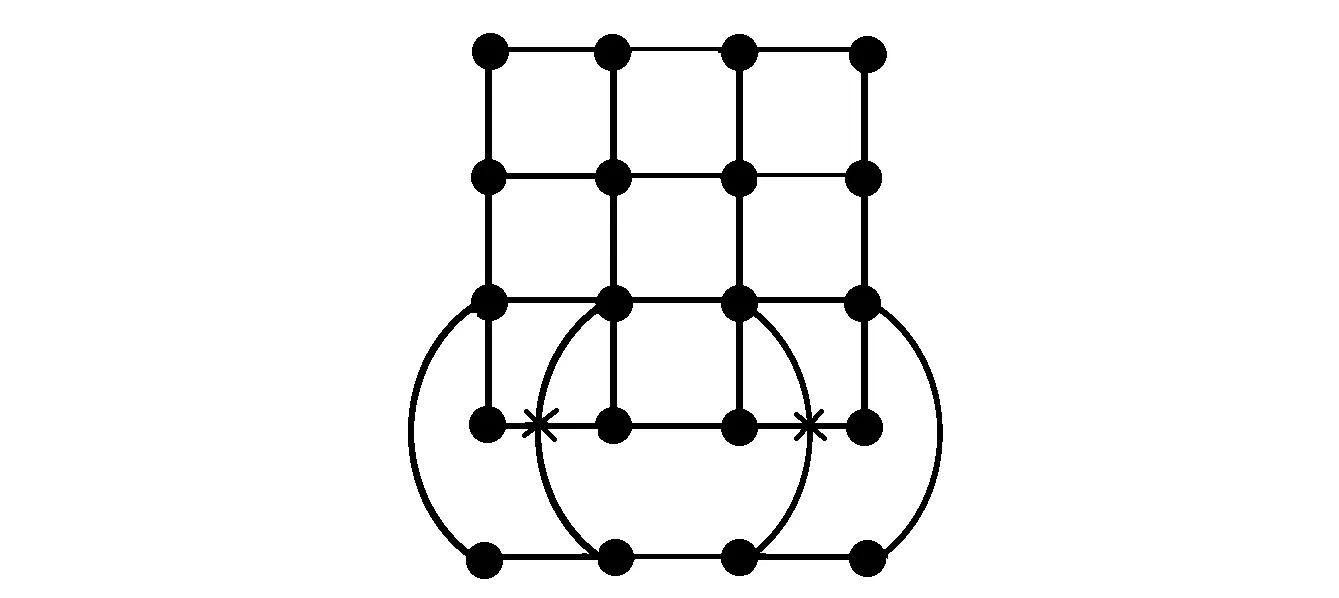
图8 T43×P3的一个好画法Fig.8 A good drawing of T43×P3
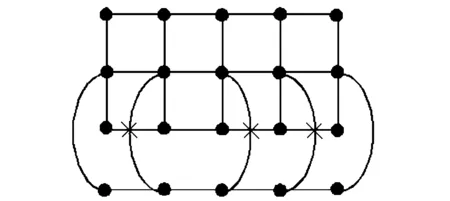
图9 T43×P3的子图H的一个好画法Fig.9 A good drawing of subgraph H of T43×P3
引理10 cr(T43×P4)=3.
证明 由T43×P4的一个好画法(见图10)可知cr(T43×P4)≤3,如果可以证明cr(T43×P4)≥3成立,则结论成立.设G表示笛卡尔积图T43×P4的其中一个子图(见图11),由引理1可得cr(T43×P4)≥cr(G).显然,子图G与S3×P4同构,由引理4可知cr(G)=cr(S3×P4)=3,所以cr(T43×P4)≥3,故有cr(T43×P4)=3.
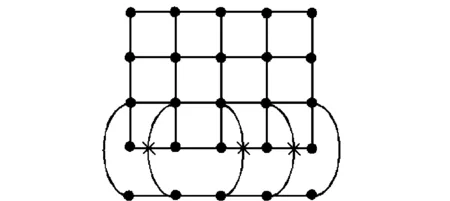
图10 T43×P4的一个好画法Fig.10 A good drawing of T43×P4
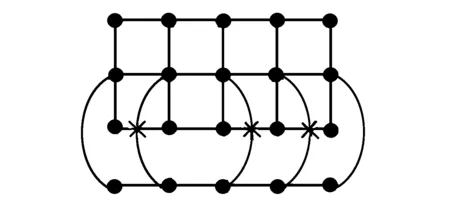
图11 T43×P4的子图G的一个好画法Fig.11 A good drawing of subgraph G of T43×P4
类似于引理9和引理10的证明方法和过程可得下面两个结果,同时可以给出关于T43×Pm的交叉数的显式表达式,即定理7.
引理11 cr(T43×P5)=4.
引理12 cr(T43×P6)=5.
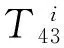
证明 因为在笛卡尔积图T43×Pm的好画法D中,树T43的每个拷贝T43i(1≤i≤m)自身都没有交叉,所以可以得到以下2个断言:
断言1 树T43的2个不同的拷贝T43i和T43j的边显然不能相互交叉.
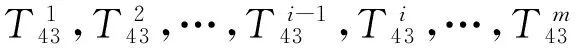
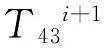
定理7 cr(T43×Pm)=m-1,m≥1.
证明 (1)由引理7至引理12可得,当1≤m≤6时,cr(T43×Pm)=m-1显然成立.
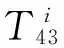
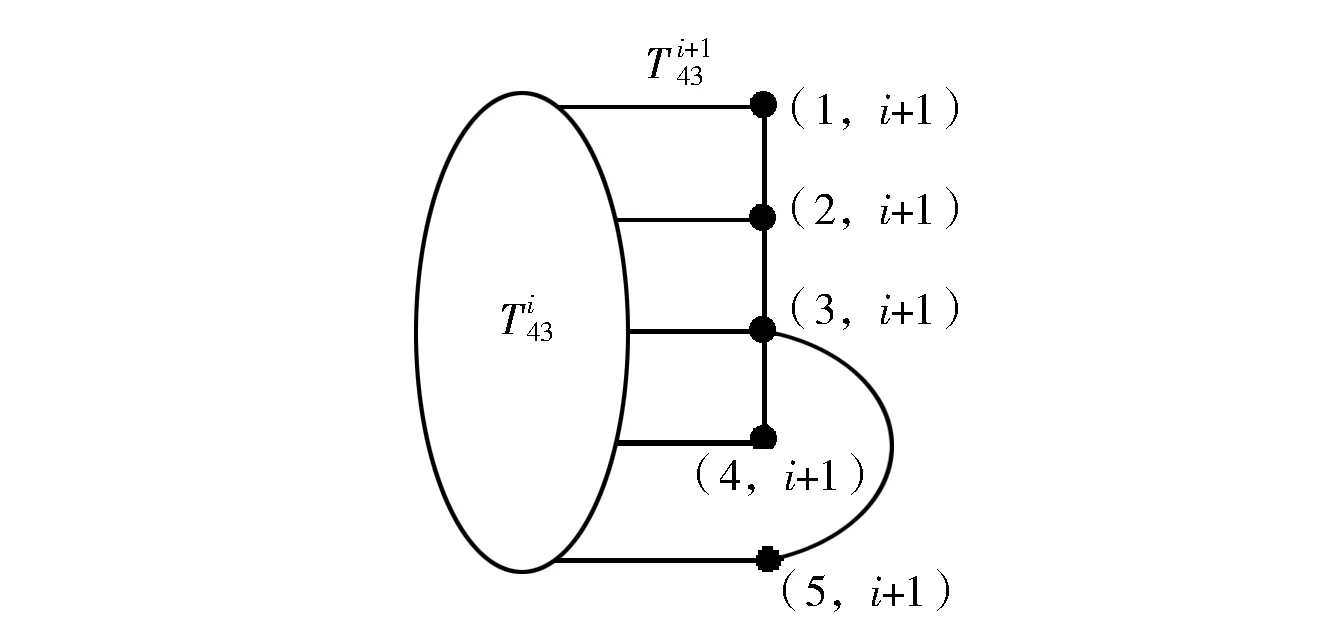
图12 引理13的证明图示Fig.12 An illustration of lemma 13
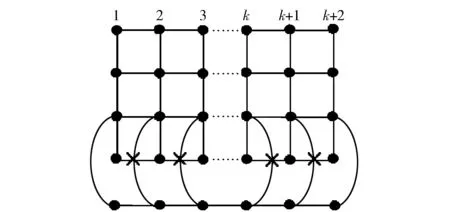
图13 T43×Pk+1的一个好画法Fig.13 A good drawing of T43×Pk+1
故命题得证,即对于m≥1均有cr(T43×Pm)=m-1成立.
[1] BONDY J A,MURTY U S R.Graph Theory with Applications[M].New York:Elsevier,1981.
[2] BENEKE L W,RINGEISEN R D.On the crossing numbers of products of cycles and graphs of order four[J].Journal of Graph Theory,1980(4):145-155.
[3] LEIGHTON F T.Complexity Issues in VLSL [M].Cambridge: The MIT Press,1983.
[4] LEIGHTON F T.New lower bound techniques for VLSL[J].Mathematical Systems Theory,1984(17):47-70.
[5] BHATT S N,LEIGHTON F T.A framework for solving VLSL graph layout problems [J].Journal of Computation for System Science,1984(28):300-343.
[6] GAREY M R,JOHSON D S.Crossing number is NP-complete[J].SIAM Journal on Algebraic and Discrete Methods,1983(4):312-316.
[7] 袁梓瀚,黄元秋,刘金旺.7阶循环图C(7,2)与Pn的笛卡尔积的交叉数[J].数学进展,2008,37(2):245-253.
[9] 袁梓瀚,黄元秋.一个六阶3-连通图与P3的笛卡尔积的交叉数[J].数学理论与应用,2007,27(2):49-51.
[10]周智勇,黄元秋.笛卡尔积图K3.3×Pn的交叉数[J].湖南师范大学学报(自然科学版),2007,30(1):31-34.
[12]BOKAL D.On the crossing numbers of Cartesian products with paths[J].Journal of Combinatorial Theory(Series B),2007(87):381-384.
[13]袁梓瀚.关于循环图及一些特殊图与路、星、树、圈的笛卡尔积的交叉数研究[D].长沙:湖南师范大学,2009.
[14]刘伟.部分联图及笛卡尔积交叉数的研究[D].长沙:湖南师范大学,2013.
[15]柯小玲.笛卡尔积图Tn×Cm的交叉数[J].闽江学院学报,2010,31(2):5-8.
On the crossing numbers of Cartesian products of treeTnwith pathPm
HU Ningbei, WEI Shouliu, BAI Yinyan
(DepartmentofMathematics,MinjiangUniversity,Fuzhou350121,China)
The enumeration problem of the crossing number in graphs is an important research subject. LetTmandPmbe a tree and a path withn+1 vertices, respectively. In this paper, we determine the crossing numbers of Cartesian product of circle graphPmwith some tree graphsTn(n≤4) by mathematical induction.
Cartesian product; good drawing; crossing number; tree; path
2017-02-20
福建省自然科学基金(2015J01589);福建省大学生创新创业训练项目(201510395050)
胡宁贝(1994-),女,河南滑县人,本科生,主要研究图论及其应用.
魏首柳(1978-),男,福建大田人,副教授,博士,主要研究图论及其应用.E-mail:wslwillow@126.com.
O157.5
A
1674-330X(2017)02-0078-05
