透过现象看本质——如何解决数学中典型问题的变式

江苏兴化市周庄中心小学 陆红梅

透过现象看本质
——如何解决数学中典型问题的变式

江苏兴化市周庄中心小学 陆红梅

小学数学中有许多经典题型，如“工程问题”“追及问题”“相遇问题”“鸡兔同笼问题”等，这些典型问题不仅能考查学生对相关知识的掌握情况，也能检测学生运用知识的灵活度和变通能力，所以在各级各类试卷中出现的频率非常高。非但如此，此类题目总是以不同的“面貌”出现，虽然无非是“换汤不换药”“新瓶装旧酒”，但是，经过一定的“易容术”后，极具迷惑性。因此，如何让学生多长个“心眼”，迅速辨识其本质，显得十分重要。

经典题型 变式 本质 规律 辨识

一次期末测验，有这样一道题：

结果，学生中大部分对工程问题很精通的“老司机”也栽在这道题目上，错误率高达60%。细细捋一下这些错误，两种犯错情况占主流：

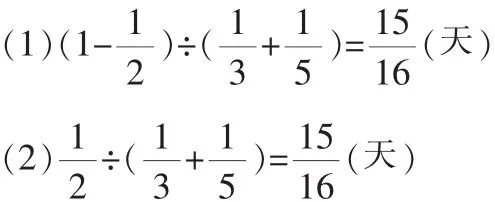
其实，这是一道难度系数不高的工程问题，主要考查工作时间、工作效率、工作任务量三者之间的数量关系。只有搞清每一步所求的问题与条件之间的关系，才能选择正确的数量关系解答。

一、卸下“伪装”条件，恰当取舍信息

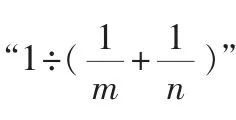
此题中“伪装”的条件有：将甲、乙两个施工队单独打通隧道所需时间数由常态下的“整数”改为分子是“1”的“分数”，然后把习惯性的“完工”改为“完成一半”。

卸下这些“伪装”，我们仍然可以透过现象看本质，死死抓住“工作任务÷工作效率=工作时间”这个“母公式”以及由此衍生出的一些“子公式”——“工作总任务÷单干工作效率=单干工作时间；工作总任务÷合作工作效率=合作工作时间；部分工作任务÷工作效率=部分工作时间”等求出正确解答。

仍然把抽象的工作总量设为单位“1”，先分别求出甲、乙两队单独施工时的工作效率，也即是甲、乙两队一天能完成的作业量，然后将两队工作效率进行数据叠加，即可得出合作时的工作效率，最后求出还有一半隧道没有打通时所用的时间。正确算式为

二、破解表象，认识问题本源

这类经典问题（工程问题）的教学，常规方法是通过对课本上一些具有代表性的简单例题的分析，归纳出一个解题模式，形成初步印象，积累一些不成熟的经验。然后学生依照模式解题，来应对一切“工程问题”，致使学生把非本质的特征误认为本质特征，甚至根本抓不住本质属性，无所适从。这次抽检中，不少学生就把题目中提供的工作时间误解为工作效率，将重要数据张冠李戴、颠三倒四，引发思维混乱。工作时间这个关键数量，在经验题型的表述中，通常为整数“m”，然后除工作总量“1”得“”。如果在我们的日常教学中能向学生提供足够多的变式题型，进行充分的变式训练，引导学生认识到多种变式的可能，就可以有效促使学生掌握本质属性。

仍以本题为例：甲、乙两个施工队单独打通隧道所需时间，可以是整数，也可以是分数和小数，甚至可以是带分数、假分数。这样可以让学生明确工作效率中的m、n可以是不同的数据。解题时，欲求甲、乙两队的工作效率则必须将1分别除以m、n。大多数变式题与原型题大体一样，只是题目中的个别条件发生了形式上的改变。关键时刻，我们一定要心细如尘，明察秋毫，看清每一句提示，可以做上记号，通过观察、对比、分析、推理、综合，审清题目给的条件和要求。

三、审视答案，发现可疑线索

解答完毕后，要养成认真检查的好习惯，确保解答的完整性和正确性。

检查绝不是简单地复核答案，查验演算是否正确，步骤是否到位，对于变式题型，检查更重要的是意味着，要从数据、事理、算理、常识等几个方面来仔细核查答案的合理性。同时，也能从小培养学生的自主架构能力。

因此，笔者认为在以后的教学中，这些问题应该引起我们的足够重视，如果能够从以上三个方面指导教学，就可以收到预期的效果。教师要随时观察学生的学习动向，找准不良症状，及时把脉问诊，特别是在面对经典题型的变式问题时，更应该未雨绸缪，在遇到变式前，多提供变式训练，增强“免疫力”，打好“预防针”。