基于Pandat的Ti-Al系相图计算及热力学评估

史忠兵，马凤仓，张全成，王 飞,3，刘 平，李 伟，刘新宽

(1.上海理工大学材料科学与工程学院，上海 200093； 2.上海材料研究所，上海 200437；3.上海材料基因组工程研究院，上海 200072)



基于Pandat的Ti-Al系相图计算及热力学评估

史忠兵1,2,3，马凤仓1，张全成2，王 飞2,3，刘 平1，李 伟1，刘新宽1

(1.上海理工大学材料科学与工程学院，上海 200093； 2.上海材料研究所，上海 200437；3.上海材料基因组工程研究院，上海 200072)

基于相图计算理论，用Pandat 2016热力学计算软件、最新的钛合金数据库和热力学模型，计算研究了Ti-Al二元系相图。从相律、相图的特殊点、各相存在的范围、相变点等方面对其进行了详细的热力学评估。计算结果表明：计算相图和实验相图吻合得较好，其相对误差基本都在5%以内，为推广到三元或更高元体系相图奠定了基础。随后提出了一个新的计算Ti-Al二元系中(α+β)/β相变点的公式，其置信度为99.982%，与经验计算公式相比，计算更为准确，具有一定的参考价值和学术交流意义。

Pandat； 钛合金数据库； 热力学模型； 相图； 评估

1 引 言

材料是国际上公认的现代文明的三大支柱之一。从现代科学技术发展史不难看出，每一种新技术的发明，往往都和新材料的发展息息相关。而合金相图是用来表示材料相状态和温度及成分关系的综合图形，其所表示的相状态是平衡状态，是研究凝固、相变、晶体生长、固态相变的基础，是选择和决定材料的配方、制备方法、加工工艺和使用条件的依据，可以指导改善和提高已有材料的性能，特别是在具有特殊功能的新材料设计研究和制备工艺方面[1-2]。因此相图被誉为材料设计的指导书、材料科学工作者的地图。实验测定相图由于受到原料纯度、实验设备精确性和人为误差等诸多因素的影响，表现出较大的局限性。再加上实验测定相图过程中需要耗费大量的时间、人力和物力，在一定程度上制约了实验相图的发展。20世纪70年代以来，相图与热化学的计算机耦合即相图计算CALPHAD(Calculation of Phase Diagram)技术迅速崛起。随着材料热力学和计算机科学的迅速发展，近年来计算相图逐步发展成为一门新兴学科[3]。目前材料科学领域已开始应用了通用的相图计算软件，如Thermo-Calc、FactSage、Pandat和JMatPro等，克服了单纯依靠实验探索研究的单一性，提高了研制效率，节约了资源和能源。CALPHAD方法与第一性原理[4-6]的结合是热力学计算的发展方向。

CALPHAD方法的成功应用依赖于可靠的计算程序和可靠的实验数据库[7]。本文采用最新的Pandat相图计算软件和最新的Ti合金数据库计算了Ti-Al二元相图，并对其进行了热力学评估。在Ti合金相变点经验计算公式的基础上，提出了一个更加精确地计算Ti-Al二元系相变点的公式。

2 热力学计算的要素和原理

材料热力学计算的三大要素是热力学计算软件、数据库和热力学模型。

2.1 Pandat软件

Pandat是20世纪80年代由美国威斯康星大学Chang教授为首的研究团队基于CALPHAD原理开发的多元热力学计算软件包。在此基础上，1996 年Y. Austin Chang 创建了CompuTherm LLC 公司，致力于运用C++语言研究Windows 界面的新一代多元合金相图和热力学性能计算软件Pandat,专门为工业、研究及教育用户提供功能强大和方便易学的相图与热力学计算软件。Pandat的最大优点是简洁易用，即使没有相图计算专业知识和计算技巧的使用者，也能在不需要预设初值的情况下，自动搜索多元多相体系的稳定相，且支持用户自定义数据库，同时该系统在自由能最小算法上对陷入局部极小进行了优化。Pandat被广泛应用于世界众多知名公司与高校中，友好的操作界面及标准、可靠的计算结果已让其得到越来越多的工程师与科研人员的青睐[8]。该系统主要适用于金属体系的相图计算，2015年10月23日发布了最新版本Pandat 2016。

2.2 Ti合金数据库

早期的数据库包含Ti，Al，B，C，Cr，Cu，Fe，H，Mo，N，Nb，Ni，O，Si，Sn，Ta，V，Zr共17中元素。现在的最新钛合金数据库，在原来数据库的基础上又添加了一种Mn元素。

2.3 原理

相图就是用来表示材料相状态和温度及成分关系的综合图形，其所表示的相状态是平衡状态，因而是在一定温度、成分条件下热力学最稳定、自由焓最低的状态[7]。

恒温恒压下，体系达到相平衡的基本判据是:体系的总Gibbs自由能最小。由于相平衡时，体系自由能需达最低值，故以优化方法求出体系自由能极小值，并以极小值时的各相成分解作为平衡相成分，即令：

(1)

式中的参数Gi，即组元i在不同相中的吉布斯自由能，也就是组元i的点阵稳定性常数，要从相关的热力学数据库中提取；Xi是不同相的摩尔分数。

由上式所示的平衡条件,衍生出任一组元的化学势在平衡共存的各相中相等的平衡判据，即：

(2)

综上所述，相图热力学计算要首先确定体系在各个温度下的吉布斯自由能对成分变化的表达式，然后借助计算机求解式(1)或(2)定义的方程组,从而得到平衡共存的各相成分。

2.4 热力学模型

相图是一种化学图形，必须通过数学模型的方式才能实现其广泛的应用[9]。而采用不同的热力学模型进行计算将产生不同的结果，进而会得到不同的相图。为了尽可能获得与实际相符合的Ti-Al二元相图，不同的相结构采用了不同的热力学模型。

(1)无序固溶相——L、α-Ti(hcp)、β-Ti(bcc)、Al(fcc)采用的模型[7]为：

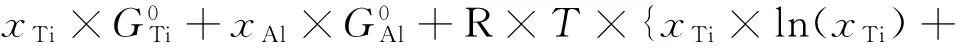
(3)

(2)有序间金属化合物相—α2-Ti3Al(D019)、γ-TiAl(L10)是由Ti组成的亚点阵1和由Al组成的亚点阵2构成的相，具有宽范围的同质性。其热力学模型即亚点阵模型[10]如下：

(4)

(3)化学计量比相——TiAl2、Ti2Al5的热力学模型[10]为：

(5)

3 Ti-Al系的相图计算及其评估

3.1 二元相图的计算

完整的二元系相图是一个三维空间，包括3个强度变量：温度(T)、压力(P)、成分(x)。一般情况只讨论恒压情况下的二元相图，因此可以用两个独立变量(温度和成分)的二维相图进行描述。利用Pandat提供的二元相图计算模块和Ti合金数据库可以计算二元合金体系下的合金成分分布及相组成，包括相图、相成分、相分数等。

Ti-Al二元相图对于Ti-Al基合金的研究具有重要的意义[11-12]，因此Ti-Al二元相图从1949年首次发表以来一直是许多研究学者研究的热点。然而，由于Ti-Al二元合金的熔点较高且其相变复杂，虽然通过相图计算与试验验证得到了大致一致的相图，但不同学者得到的相图在一些细节上仍有较大的出入。因此对其进行准确的热力学计算和详细的评估具有非常重要的研究意义。

从图1可以看出：Ti-Al二元合金总共存在着9个相。根据其结构组成不同分为三类：无序固溶相：L(Liquid)、α-Ti(Hcp)、β-Ti(Bcc)、Al(Fcc)；有序间金属化合物相：α2-Ti3Al(D019)、γ-TiAl(L10)；化学计量比相：TiAl2、TiAl3(DO22)、Ti2Al5、Ti5Al11。

图1 本工作计算的Ti-Al二元平衡相图Fig.1 Ti-Al binary phase diagram calculated by this work

钛合金中的合金元素以固溶体或是化合物的形式存在，主要取决于原子的电子层结构、原子半径大小、晶格类型、电负性及电子浓度等因素。Ti和Al元素的外层电子结构和原子半径如表1所示。

表1 Ti和Al元素的外层电子结构和原子半径Table1 Outer electronic structure and atomic radius of Ti and Al

Al元素是钛合金中最为重要的合金元素，在Ti-Al相图(图1)中：当铝当量含量较低时，主要沉淀出α2-Ti3Al(D019)有序相，当铝当量含量较高时，有γ-TiAl(L10)及其他钛铝化合物形成，在正常使用的含铝钛合金中以α2沉淀强化为主，所以α2相为钛合金中一个极为重要的有序相。α2相与α相的根本区别在于，α相是无序固溶相，而α2相是长程有序相。α2相是在α相基础上形成的长程有序相，该转变过程如图2所示。当Al原子进入α相的晶格，形成Al在α晶格中的固溶体后， Al原子开始是以无序状态存在的，虽然此时化学成分与α2相(Ti3Al)相同，但结构属于无序α相，随着保温时间的延长或无序α相以较慢的速度冷却，Al原子在固溶体中的分布趋于有序状态，形成长程有序相(DO19空间群) α2相。

3.2 热力学评估

3.2.1 相律的评估 相律是研究相平衡的基本规律，表示平衡物系中的自由度数、相数及独立组分数之间的关系，其计算公式为：

(6)

式中：C为组分数，P为共存相数，自由度f为条件自由度。

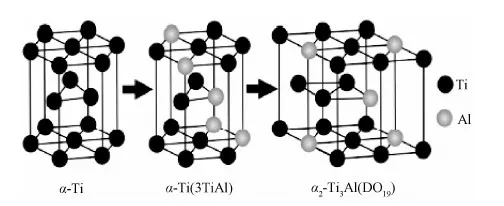
图2 α相转变为α2相的过程[13]Fig.2 Transformation from α to α2[13]

对二元系，C=2，f=3-P，最多平衡共存相数为3。从图1可以看出，Ti-Al二元系最多有3个平衡共存相，符合相律。

3.2.2 特殊点的评估 通过对大量文献报告[14-29]的研究，并结合自身的工作，获得了Ti-Al二元相图中一些特殊点的实验数据。本文利用实验数据、计算数据与文献中实验数据对比做成了表2和图3。从中可以看出：计算值与实验值的最大偏差绝对值为30.87℃，最小偏差绝对值为0.131℃；相对误差最大值为2.18024%，最小值为0.01814%。相对误差均小于5%，可见，通过Pandat计算出的Ti-Al二元相图和实验相图吻合得较好。

3.2.3 相存在范围的评估 从Ti-Al晶体结构数据(表3)中可看出：计算值与实验值的最大偏差绝对值为5.9%，最小偏差绝对值为0；相对误差最大值为11%，相对误差最小值为5%。除个别点外，相对误差均小于5%，可见通过Pandat计算出的Ti-Al二元相图是可靠的。因为Ti合金中Ti极易被氧化，而氧的含量对于一些相(如TiAl相)的相对稳定性影响作用很大。致使计算的Ti-X相平衡关系在实验验证过程中由于O的参与而变为Ti-X-O的相平衡关系。因此个别点误差较大的原因可能是O导致的。

图3 Ti-Al二元相图和实验点Fig.3 Ti-Al phase diagram and experimental points

表2 Ti-Al二元平衡相图的特殊点Table 2 Special Points of the Ti-AI binary phase diagram

表3 Ti-Al晶体结构数据Table 3 Ti-Al Crystal Structure Data

3.2.4 相变点的评估 钛及钛合金的(α+β)/β相变点的确定是热加工及热处理的一个重要参数，只有先准确地确定出相变点，才有可能选择最为合适的热加工以及热处理工艺。目前，多数钛合金国家标准中规定了有关钛合金相变点的范围，材料厂家提供材料材质单中的相变点区间必须在标准规定的范围内。因此，对(α+β)/β相变点的评估具有重要的意义。

计算法是测试钛合金的相变点常见的方法之一[30]。它是人们依据大量的实验数据总结出来的利用钛合金中各个元素对其相变点的影响程度来近似计算相变点的一种方法，对于确定 (α+β)/β相变点有一定的参照价值。其计算公式如下：T(α+β)相变点=882℃+∑各元素含量×该元素对其的影响

(7)

式中882℃为计算纯钛时的相变点。

通常设计钛合金时，要加入3%～6%(wt,%)的Al元素，因为Al原子可以替代钛合金中α相和β相晶格中的Ti元素，形成固溶体来强化合金，并且在热处理时能够增加α相的析出量，使合金的时效强化的效果更强。但铝含量超过7%(wt,%)后，易形成脆性的Ti3Al相，降低材料的机械性能[31]。表4中各种主要元素及杂质元素的含量都在一定的范围之内，而且元素含量的波动范围也均在表5中常见合金元素和杂质含量的范围中。因此根据以上计算公式和表4中各种合金元素对钛合金相变点的影响，可以近似计算出不同成分的Ti合金的相变点。其中Al对相变点的影响为：

T(α+β)相变点=

(8)

图4 经验计算公式计算的相变点与本工作计算结果的对比Fig.4 Comparison of phase transition points between emprical formula and this work

钛合金的α+β→β转变是个持续的过程，当合金随着温度的升高会不断地有α相转变为β相，直到接近转变温度时所有α相均变成了β相，这与纯金属熔化或者同素异构体的转变过程中的相变温度总是保持恒定不变的情况是不同的，因此转变完成时的温度才是钛合金的相转变温度[34]。将利用经验公式计算的相变点和利用Pandat软件计算的相变点进行对比，如图4所示。当Al的百分含量在0～2时，二者计算的相变点误差随着Al含量的增加而增大，最小误差：882-881.84=0.16℃，最大误差：933.92-911=22.92℃；当Al的百分含量在2～7时，二者计算的相变点误差随着Al含量的增加而减小，最小误差：1037.09-1026=11.09℃，最大误差：933.92-911=22.92℃。

总体上讲利用经验公式计算的相变线在本工作计算值之下，这可能是由于Ti合金中的杂质元素造成的。钛的化学活性大，与大气中O、N、H、CO、CO2、水蒸气、氨气等产生强烈的化学反应。从表4可以看出：杂质元素C、O、N均可以提高钛合金的相变温度，属于α相稳定元素。由此可以推测，实验用的钛合金可能含有C、O和N中的一种或几种，尤其可能含有O。

表4 元素含量对钛合金相变点的影响[32]Table 4 Effect of element content on phase transition points of titanium alloy[32]

表5 钛合金中常见的合金元素和杂质元素含量[33]/wt%Table 5 Common alloying elements and impurities in titanium alloys[33] /wt%

由于经验计算法是根据人们之前总结出的合金元素对钛合金的影响程度而得到的，它对合金相变点的确定有着一定的参考意义，但是合金实际成分对合金相变点起决定性作用。在制备合金时，存在的微量杂质元素会对合金的相变点产生一定的影响。而Pandat计算出来的相变点是建立在大量实验数据基础上的，为了找到更精确的Ti合金相变点的计算公式，提取了用Pandat计算的相变点。如图5所示，用OriginPro 8.5拟合出了对应的计算公式。其置信度为99.982%，说明拟合结果和实验数据吻合性良好。

图5 Ti-Al相变点的多项式拟合Fig.5 Polynomial fit of Ti-Al Phase transition points 4 结 论

利用Pandat 2016软件和最新的钛合金数据库，对数据较为充分的Ti-Al二元相图进行了计算和评估，得到如下结论：

1.介绍了热力学计算软件、数据库、原理和模型。

2.利用Ti合金数据库和热力学模型并遵循相图计算流程对Ti-Al二元相图进行了计算。

3.利用实验数据对用Pandat软件计算的Ti-Al二元相图的特殊点(如共晶点、包晶点等)进行评估，相对误差均小于5%，说明了计算相图和实验相图吻合性良好。

4.利用实验数据对计算出的各相存在的范围进行了评估，除个别点外，相对误差基本都在5%以下，说明计算出的二元相图是可靠的。

5.利用经验计算公式对用Pandat软件计算的Ti-Al的相变点进行了评估，发现计算结果和经验公式计算的结果相差不大，但仍有一定程度的偏差。进而提出了一个置信度为99.982%的计算Ti-Al相变点的计算公式。

6.CAPHAD法得到的是热力学物理模型，因此可以由尽量少的实验数据点得到温度、组成区域尽量多的信息，且可由二元外推到三元体系和多组分体系，预计体系的一些不易测定的性质，包括复杂多组分体系的相图计算，确定体系的平衡条件，比其它热力学计算方法更为可靠。

[1] 乔芝郁, 郝士明. 相图计算研究的进展[J]. 材料与冶金学报, 2005, 4(2): 83～91.

[2] 刘炜丽, 王博文, 孙德志. Fe-Co-(Sm,Dy)系三元等温截面图[J]. 材料科学与工程学报, 2009，27(2): 178～181.

[3] 武月春, 陈敬超, 彭平,等.基于Pandat软件的相图计算及其方法概述[J]. 热加工工艺, 2014, (12): 103～106.

[4] 吴东海, 童张法, 等. 以第一性原理研究CaCO3的表面能与电子结构[J]. 材料科学与工程学报, 2015, 33(6):857～861.

[5] 田景芝, 张苹, 荆涛, 等. 浓度对Al掺杂TiO2电子结构影响的第一性原理计算[J]. 材料科学与工程学报, 2014, 32(3): 349～352.

[6] 王峰, 孙士杰, 于波, 等. Mg-Al-Ca-Sn合金中二元相金属间化合物结构稳定性、电子结构、弹性性质和热力学性质的第一性原理计算(英文)[J]. Transactions of Nonferrous Metals Society of China, 2016, (1):203～212.

[7] Chen S L, Daniel S, Zhang F, et al. The PANDAT Software Package and its Applications[J]. Calphad, 2002, 26(2): 175～188.

[8] Panda Software. http://www.computherm.cn/home/PanSoftware. php.

[9] 郭思斯, 黄民, 等. CALPHAD应用于有机体系热力学相平衡/相图的计算[J].计算机与应用化学, 2008, 25(3):323～328.

[10] Kattner U R, Lin J C, Chang Y A. Thermodynamic Assessment and Calculation of the Ti-Al System[J]. Metallurgical Transactions A, 1992, 23(8): 2081～2090.

[11] 吴丹, 邵爱民. 5010H19铝合金百叶窗带材生产工艺研究[J].上海有色金属, 2015, 36(4): 163～166.

[12] 冯静, 丁冬雁, 张俊超, 等. Ti元素对7072铝合金显微组织与性能的影响[J].上海有色金属, 2013, 34(1): 1～6,14.

[13] 辛社伟, 赵永庆. 钛合金固态相变的归纳与讨论(Ⅵ)——阿尔法[J].钛工业进展, 2013, 30(4): 1～8.

[14] Fink W L, Van H, Budge P M. Constitution of High-Purity Aluminum-Titanium Alloys[J]. Transaction of American Institute of Mining, Metallurgical, and Petroleum Engineers, 1931, 93: 421～439.

[15] Bumps E S, Kessler H D, Hansen M. Titanium-Aluminum SystemTrans[J]. Transaction of American Institute of Mining, Metallurgical, and Petroleum Engineers, 1952, 194:609～614.

[16] Blackburn M J. The Ordering Transformation in Titanium: Aluminum Alloys Containing up to 25 at. pct Al[J]. Transaction of American Institute of Mining, Metallurgical, and Petroleum Engineers, 1967, 239:1200～1208.

[17] Cisse J, Kerr H W, Bolling G F. The Nucleation and Solidification of Al-Ti Alloys[J]. Metallurgical and Materials Transactions, 1974, 5:633～641.

[18] Heckler M. Solubility of Titanium in Liquid Aluminium[J]. Aluminium, 1974, 50(6): 405～407.

[19] Shibata K, Sato T, Ohira G. The Solute Distributions in Dilute Al-Ti Alloys During Unidirectional Solidification[J]. Journal of Crystal Growth, 1978, 44: 435～445.

[20] Collings E W. Magnetic Studies of Phase Equilibria in Ti-Al (30 to 57 At. Pct) Alloys Metall. [J]. Metallurgical and Materials Transactions A, 1979, 10: 463～474.

[21] Abdel-Hamid A, Allibert C H, Durand F, Z. Equilibrium between TiAl3and Molten Al: Results from the Technique of Electromagnetic Phase Separation[J]. Zeitschrift Fur Metallkunde Metallkd, 1984, 75: 455～458.

[22] Shull R D, McAlister A J, Reno R C. Phase Equilibria in the Titanium-Aluminum System[J]. Titanium Science and Technology, 1985,3:1459～1466.

[23] Murray J L. Phase Diagrams of Binary Titanium Alloys[J].ASM International, 1987,354.

[24] Waterstrat R M. Effect of Interstitial Elements on Phase Relationships in the Titanium-aluminum System[J]. National Institute of Standard and Technology (US) Report, 1988, 3: 1～53.

[25] Kaltenbach K, Gama S, Pinatti D G, Schulze K. A Contribution to the Al-Ti Phase Diagram[J]. Zeitschrift für Metallkunde Metallkd, 1989, 80: 511～514.

[26] McCullough C, Valencia J J, Levi C G, Mehrabian R. Phase Equilibria and Solidification in Ti-Al Alloys[J]. Acta Metallurgica, 1989, 37(5): 1321～1336.

[27] Schuster J C, Ipser H. Phases and Phase Relations in the Partial System TiAl3-TiAl[J]. Zeitschrift fur Metallkunde Metallkd, 1990, 81(6): 389～396.

[28] Mishurda J C, Perepezko J H. Phase Equilibria in Ti-Al Alloys[J]. Microstructure/property Relationships in Titanium Aluminides and Alloys, 1991,3～30.

[29] Kattner U R, Lin J C, Chang Y A. Thermodynamic Assessment and Calculation of the Ti-Al System[J]. Metallurgical and Materials Transactions A, 1992, 23(8): 2081～2090.

[30] 中华人们共和国国家标准. 钛合金β转变温度测定方法[S]. GB/T 23605-2009.

[31] 赵永庆, 陈永楠, 等. 钛合金相变及热处理[M].第一版, 长沙:中南大学出版社, 2012, 6.

[32] 《稀有金属材料加工手册》编写组.稀有金属材料加工手册[M].北京:冶金工业出版社, 1984, 48.

[33] 孙书英, 邓超. 基于二元相图精确计算钛合金α+β/β相变点[J].钛工业进展, 2011, 28(03): 21～25.

[34] 李玉涛, 耿林, 徐斌, 等. TC11钛合金相变点的测定与分析[J].稀有金属, 2006, 30(2): 231～234.

Thermodynamic Calculation and Assessment of Ti-Al System Based on Pandat

SHI Zhongbing1,2,3， MA Fengcang1， ZHANG Quancheng2， WANG Fei2,3，LIU Ping1， LI Wei1， LIU Xinkuan1

(1.University of Shanghai for Science and Technology, Shanghai 200093, China; 2.Shanghai Research Institute of Materials, Shanghai 200437, China; 3.Shanghai Institute of Materials Genome, Shanghai 200072, China)

Phase diagram of Ti-Al system was researched through the calculation using Pandat 2016 thermodynamic calculation software, the latest database of Ti alloy and reasonable thermodynamics models based on Phase diagram calculation theory. The calculated phase diagram was then assessed by phase rule, by analysing the specific points of the phase diagram, the phase areas, the phase transition points and so on. The calculated results show that the calculated phase diagram matches experimental phase diagram very well, laying a foundation for extrapolated phase diagram of ternary system and more. Their relative errors are almost below 5%. As compared with the empirical formula for (α+β)/β phase transition points of Ti-Al system, the new calculated formula proposed is more accurate, having some reference value and academic significance. Its confidence level is 99.982%.

Pandat； Titanium alloy database； thermodynamic model； phase diagram； assessment

1673-2812(2017)03-0368-07

2016-03-04；

2016-04-22

上海市科学技术委员会科研计划《Ti合金材料与材料基因组数据库建设》资助项目(14DZ2261202)

史忠兵(1988-)，硕士研究生，主要研究方向: 钛合金。E-mail: 762928105@qq.com。

马凤仓，副教授，硕导，E-mail: mafengcang@163.com。

TG111.5

A

10.14136/j.cnki.issn 1673-2812.2017.03.005