K型图的建立和应用

江苏省苏州市相城区东桥中学 凌 健

K型图的建立和应用

江苏省苏州市相城区东桥中学 凌 健

一、基本K型图

K型图又称为一线三等角图形，因图形形似字母K而得名，它有如下3种基本形式：

我们不难发现它们的共性：一直线上有3个点B、C、D，且∠B=∠ACE=∠D，可以推出∠A=∠ECD，进而得到△ABC∽△CDE.若AC=CE，则△ABC≌△CDE.我们把满足以上条件的图形称为K型图.

案例1：如图1，点E为BC上任意一点，∠B=∠AEF=∠C=90ο，求证：△ABE∽△ECF.

图1

分析：本题是一个显性模型，直接应用K型图进行解题.

证：∵∠B=90ο，∴∠BEA+∠A=90ο，

∵∠AEF=90ο，∴∠BEA+∠FEC=90ο，

∴∠A=∠FEC.

又∵∠B=∠C=90ο，

∴△ABE∽△ECF.

图2

变式：如图2，在Rt△ABC中，∠BAC=90ο，AB=AC=2，点D在BC所在的直线上运动，作∠ADE=45ο（A、D、E按逆时针方向运动）.若点D在线段BC上运动，DE交AC于E.求证：△ABD≌△DCE.

分析：本题与案例1类似，首先根据∠BAC=90ο得出∠B=∠C=45ο，从而得出∠B=∠C=∠ADE=45ο，再通过类比思想应用K型图进行解题即可.

总结：从案例1及其变式可以看出，虽然基本K型图有3种，但究其本质，可以归纳为：满足一直线上有3个角相等的图就是K型图.这3个角无论是锐角、钝角还是直角，结论都成立.为了方便，下面笔者仅用3个90ο的等角模型加以说明.

二、K型图的基本变形及推广

K型图因形似字母K而得名，但在解题的过程中我们可以发现，它也不都是以K型出现的.在有些题目的条件当中往往出现3个相等的角，但它们未必在同一直线上，是不是也可以用K型图来解呢？下面我们就来研究一下K型图的基本变形和推广.

基本变形1：已知∠ADB=∠ADC=∠BAC=90ο，根据同角的余角相等可得∠B=∠DAC，进而得出△ABD∽△CAD.事实上这是一个双垂直图形，我们可以得出△ABD∽△CAD∽△CBA，进一步可以推出射影定理.

基本变形2：已知∠ADB=∠AEC=∠BAC=90ο，根据同角的余角相等可得∠B=∠EAC，进而也能得出△ABD∽△CAE.事实上，基本变形1是基本变形2的一种特殊形式，即当CE和BD在同一直线上的情况.

基本变形3：已知∠DAE=∠BAC=90ο，根据同角的余角相等可得∠BAD=∠CAE，又因为∠D=∠E，得出△ABD∽△ACE.

总结：从以上3个基本变形我们可以发现，K型图具有很多种不同形式，它的基本变形也不仅仅是以上3种，只要满足3个或3个以上等角的图形，我们都可以考虑是否可以用K型图加以解决.

案例2：如图3，在Rt△ABC中（∠C＝90ο）放置边长分别3、4、x的3个正方形，则x的值为（）.

A.5B.6C.7D.12

图3

分析：本题是K型图的变形和推广，利用两次基本变形可得△DEF∽△GHI，建立边的关系.

解：∵∠DEF=90ο，∴∠FDE+∠DFE=90ο，

∵∠EFG=90ο，∴∠DFE+∠CFG=90ο，

∴∠FDE=∠CFG.

同理可得∠HGI=∠CFG.

∴∠FDE=∠HGI.

又∵∠DEF=∠GHI=90ο，

∴△DEF∽△GHI，

【评析】仅凭直觉解本题比较困难，学生在解题的过程中错误率比较高.若能发现此题为K型图的基本变形便能很快突破难点，解决问题.

案例3：如图4，在平面直角坐标系中，已知点A、B的坐标分别为（8，0）、（0，2），C是AB的中点，过C作y轴的垂线，垂足为D.动点P从点D出发，沿DC向匀速运动，过点P作x轴的垂线，垂足为E，连接BP、C.当BP所在直线与EC所在直线第一次垂直时，点P的坐标为.

分析：当BP所在直线与EC所在直线第一次垂直时，添加辅助线，延长BP交线段CE于点F，如图5.此时∠CPE=∠PFC=∠BDP=90ο，虽然它们不在同一直线上，但符合K型图的推广的条件，进一步分析验证模型推理的正确性，进而可以得出△BDP与△EPC相似.

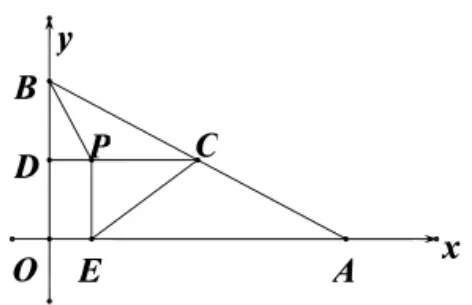
图4

图5

由于题目要求BP所在直线与EC所在直线第一次垂直，故可得出DP比BD短时，两者第一次垂直。所以本题只需要讨论△BDP∽△CPE这一种情况.

∴a2-4a+3=0.

【评析】本题是2016年苏州市中考数学卷的填空压轴题，学生得分情况不理想.究其原因，还是学生缺乏将实际问题转化为基本图形的能力，对K型图的基本变形缺乏本质的认识.

三、K型图的建立方法和应用

在有些题目中，K型图或其基本变形并没有直接给出，而是需要学生根据题目的条件特征和图形特征自主构造，建立模型，这是一个难点.

如果条件中含有垂直这个几何条件，可以考虑构造K型图.K型图的构建总体上分为两类.

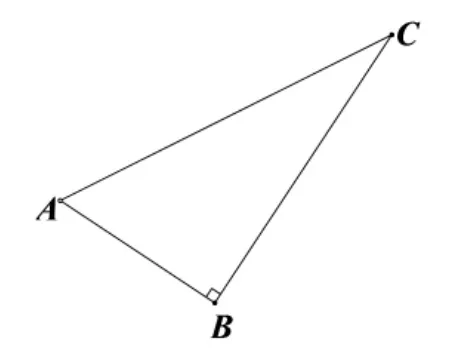
图6

图7

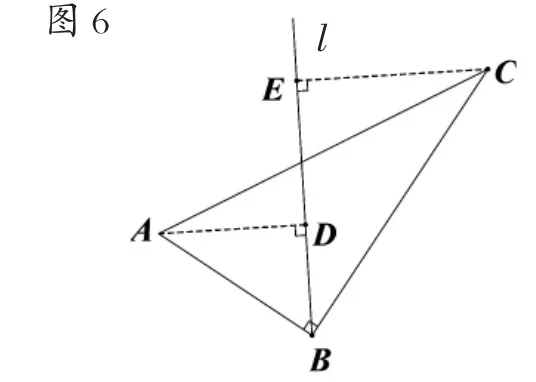
图8

如图6，若∠B=90ο我们可以过直角两边上的任意一点向经过直角顶点的直线作垂线，构建K型图.

如图7，直线l在直角∠ABC的外部，因此所得K型图称为外K型.

如图8，由于直线l在直角∠ABC的内部，因此所得K型图称为内K型.

图7和图8均可以证出△ABD∽△BCE，从而把垂直转化为线段间的数量关系.一般在构造K型图过程中，我们都可以将图形构造为外K型和内K型两种.基本图形的构建是关键，也是提高学生探究能力和创新精神的必由之路.

案例4：如图9，直线l1、l2、l3互相平行，且l1、l2的距离为1，l2、l3的距离为2，等腰△ABC的3个顶点分别在3条平行线上，AB=AC，∠BAC=90ο，求等腰△ABC的腰长.

分析：本题已知∠BAC=90ο，考虑是否可以建立K型图解题.又知道是经过直角顶点A的直线，故有了建立外K型图的思路.

图9

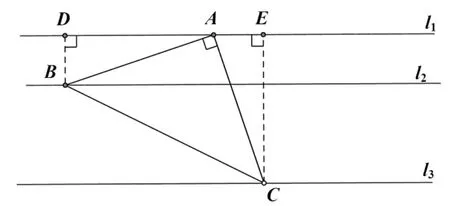
图10

解：过点B、C分别作直线l1的垂线，垂足为D、E，如图10，不难证出△ABD≌△CAE，

∴AD=CE=3.

又∵DB=1，

变式：如图11，直线l1、l2、l3互相平行，且l1、l2的距离为1，l2、l3的距离为2，等腰△ABC的3个顶点分别在3条平行线上，AB=AC，∠BAC=120ο，求等腰△ABC的腰长.

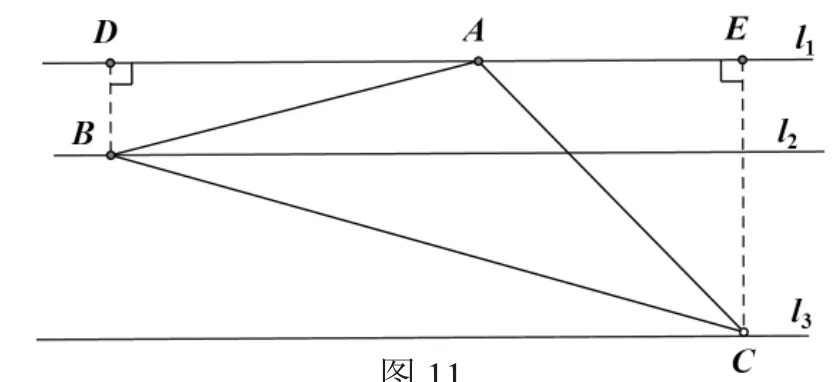
图11

图12

分析：本题受案例4的启发，过点B、C分别作直线l1的垂线，垂足为D、E.但这时并没有构成K型图，解题陷入僵局.

当然，想要解决本题，还是要向构建K型图的方向努力，所以有了如下思路.

解：在l1上取点F，连接BF，使得∠AFB=120ο，

在l1上取点G，连CG，使得∠CGA=120ο，如图12.

因为∠AFB=∠BAC=∠CAG=120ο，

不难证出△ABF≌△CAG.

【评析】本变式题的模型结构不明显，学生首先会想到作垂线，但作完垂线以后解题又无法进行下去了.根据最近发展区理论，让学生稍微跳一跳，笔者认为他们还是能够构造出3个120ο角的K型图的.

编辑/王一鸣E-mail：51213148@qq.com