执勤行车时间的KMP- RBF融合预测方法*

金杉 金志刚 刘永磊

(1. 天津大学 电气自动化与信息工程学院，天津 300072; 2. 天津市公安消防局，天津 300020)

执勤行车时间的KMP- RBF融合预测方法*

金杉1，2金志刚1刘永磊1

(1. 天津大学 电气自动化与信息工程学院，天津 300072; 2. 天津市公安消防局，天津 300020)

针对执勤车辆沿某一路径行驶时长难以预测的问题，文中提出一种KMP- RBF融合方法，采用GPS定位、悉尼自适应交通控制系统(SCATS)线圈作为融合信号源，建立路况信息选择融合模型，将模糊推理知识表达、MAPSO算法寻优和RBF网络训练相结合，自适应优化系统关键参数，从训练数据库匹配适用时间、空间数据.实验中，使用交通监控系统实测实验用车行驶时长数据，并与预测数据进行对比，从误差率、算法迭代与精确度方面证明文中方法是高效而可靠的．

信息融合; 预测; 模糊推理;多智能体粒子群优化算法;RBF神经网络;k-均值算法;执勤行车时间

现代城市中，救护、消防、工程抢险等执勤车辆行驶存在3个特点: ①调度出发时点不确定，以最短时长抵达现场为首要目标; ②单次行车起止地点确定，而路线不确定; ③较其他车辆优先通行，行驶速度高于当前路段车流平均值[1].近年来，由于城市快速发展而出现的局部交通问题日趋严重，导致诸多紧急事故的延时处置[2].因此，根据不同时刻的拥堵程度，精确预测行驶时长，选择最快到达终点的路线，是当前亟待解决的问题．

目前，预测行车时间的方法主要呈现人工智能算法与多源信息融合两个特点. 李惠兵等[3]从悉尼自适应交通控制系统(SCATS)线圈、浮动车载GPS采集数据分析得到交通流密度和样本量，输入到BP网络，预估和优化城市干道行车时间准确度.相似地，杨兆升等[4]则考虑了地形和遥感数据采集，连同浮动车载GPS一并输入到BP网络融合，预估交通事故或恶劣天气环境下的行车时间.李清泉等[5]使用浮动车载和数据地图匹配，挖掘可靠行车时间.在此基础上，李宇光等[6]进一步使用海量浮动车数据匹配地图，实现电子地理系统GIS与浮动车载GPS数据之间的融合，得到最短时间路径.Mehmet等[7]将瓶颈识别与高斯混合模型融合，匹配拥堵地图和速度估计曲线阈值，搜索预估高速公路行车时间.可见，上述基于多源的人工智能信息融合算法收敛性好，数据来源较为充足，增强了人工智能方法的可解释性[8].但是上述方法也存在对时点的车速差异考虑不足、人为确定算法参数等问题，对不同时段车流变化较大的路况的分析存在不足，影响了行车时间求解的准确度[9].由此，选用多样化的监测采集方式，对融合系统进行已有训练数据的优化调整， 将有效提高时间预测精确度，有助于选择最优路线[10- 11]．

文中提出一种基于k-均值多智能体粒子群优化的径向基函数(KMP- RBF)网络多源信息融合的解决方法.采用浮动车载GPS和SCATS系统监测采集以往行车数据,设计一种改进后的径向基函数;采用具有量子与模糊改进的多智能体粒子群优化(MAPSO)算法调整神经元权重，以k-均值聚类确定径向基中心，并以关键参数模糊变化范围取代人为设置.

1 准备工作

如图1所示，文中将SCATS线圈、浮动车载GPS作为融合信号源;将交通视频监控数据作为实验用车的真实值.其中，将SCATS线圈和交通视频监控集成为检测器组，设置在各路段出口停车线位置.监控摄像头设置在高于地面5 m的位置，覆盖和识别从停车线发出的车辆;SCATS信号源位于停车线地表，向上监测行车数据．

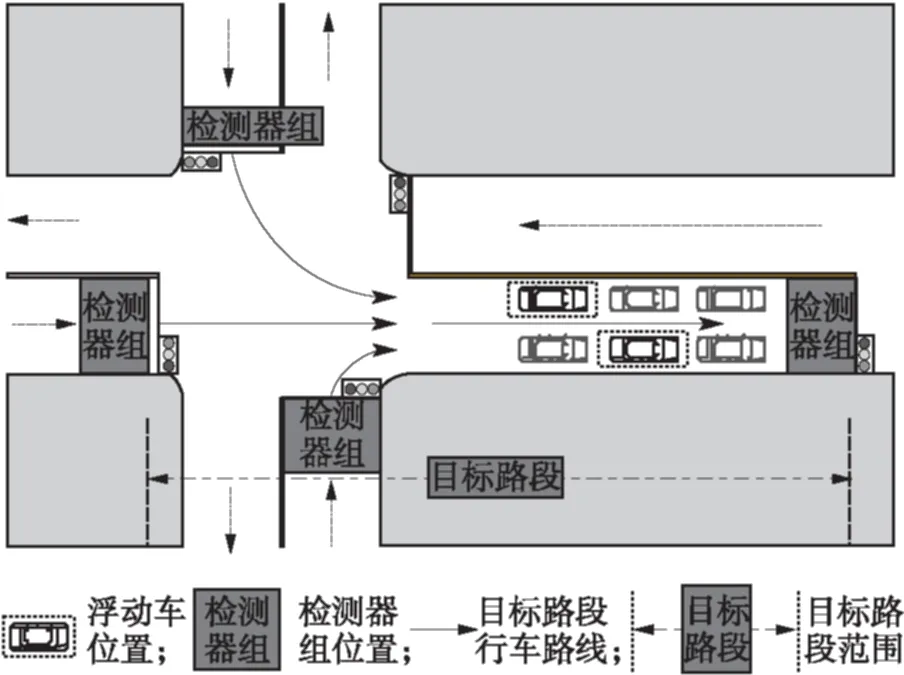
图1 目标路段范围及检测设备位置

1.1 数据采集

1.1.1 浮动车载GPS

通过数理统计抽样得到估算路段行车时长用到的浮动车数量下限:

(1)

式中：Zα/2是置信水平为1-α时相应的高斯分布变量；B是给定变异系数；V为平均速度，e为其允许的相对误差．

1.1.2 SCATS系统

设现实采样时间为绿灯信号相位，间隔为TSi;可调采样时间由人为设定.已知现实采样时点相距i的平均车头时长间距tHSi，可调采样时点相距β，位于现实采样时点相距i内的部分时长为ti，第β个可调采样时点相距包含现实采样时点相距的个数为M，则同一个监测周期中，qSi是现实采样时点相距单位时长TSi对应的抵达车数．

QSi,out=qSi/TSi

(2)

式中，QSi,out即为交通量.可调采样时点相距β的平均车头时距为

(3)

1.2 时间匹配

将前述信号分别开展时间离散化调整，使各数据源取自同一时间段内.从各信号源每日相同时段监测的T时间段内多次采样得到初始检测数据，采用对四维向量滤波的均方根方法整理:

(4)

式中：FT是某一目标路段连续采样的行车时间；fT(tk)是第k时点滤波后信号，存在fT(tk)={t,Nf,tβ,QSi,out}T,j;nsp为连续T时间内采样检测次数，t为在各类公交车辆上配备车载GPS终端得到的目标路段车辆行车时间，Nf为浮动车样本量;tβ为SCATS线圈检测采取连续多时点实测得到的平均车头时距．

1.3 空间匹配

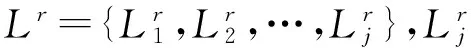
(5)

2 融合模型的建立

2.1 融合模型

已知单路径行车时间模型的输入量包括SCATS线圈、浮动车载GPS共4项样本数据，即输入层神经元数量为4.隐含层神经元为训练数据点.文中采用经验公式确定隐含层节点数:

(6)

式中：h是隐含层神经元数;m是输入神经元数;n是输出神经元数；a∈[0,10]，通常取a=2．

由式(6)可知隐含层神经元数为h=5.如图2所示，文中提出的方法网络模型结构是4- 5- 2．

图2 KMP- RBF网络模型结构

1)输入层:

X(i)=(x1(i),x2(i),x3(i),x4(i))

(7)

式中:x1(i)为目标路段平均车头时距;x2(i)为目标路段流量;x3(i)为浮动车样本量;x4(i)为浮动车行车时间估值．

2)隐含层:

文中径向基函数φ(Xk,Ci)采用经典的高斯分布函数:

φ(Xk,Ci)=φ(‖Xk-Ci‖)=

(8)

(9)

式中，k是训练样本数，dmax是各中心之间最大距离，Xk是第k个样本，Ci为基函数的中心．

3)输出层:

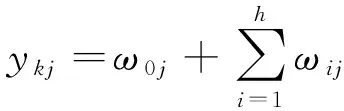
(10)

式中:ykj为融合后的路径行车时间；ωij为隐含层到输出层的权重.x5(i)为目标路段交通视频监控实测行车速度，直接作用于输出层神经元Y2.由于本算法中，输出神经元Y1较Y2输入项目仅缺少一项新加入的x5(i)，且Y2中目标路段行车时间与Y1完全相同，可以确定ωi1=ωi2，记作ωi．

神经元Y2输出预测误差率，由隐含层计算和交通视频监控实测数据x5(i)对比产生，比较出预测与真实值的接近程度，以相对误差表示．

(11)

式中，Aj是预测误差率，tout,j是预测行车时间，treal,j是交通视频监控检测的真实时间．

当预测误差率Aj大于某一预设值ε时，预测行车时间反馈至数据融合系统进行计算;反之，则预测行车时间作为合格解输出．

2.2k-均值算子

文中隐含层学习算法使用自组织选取中心方式，以长期监测数据训练各径向基神经元，采用k- 均值聚类算法，自适应优化各学习中心Ci，再建立Ci与dmax之间的关系，由式(9)得到标准差σ.假设有I个中心，第n次迭代的第i个中心是Ci(n),i=1,2,…,I.I值需要根据经验确定，为确保隐含层各神经元计算量均衡，文中方法设置聚类数I与隐含层神经元数h相等．

随机选择I个不同的输入样本为初始中心Ci(0)，随机抽取训练样本Xk作为输入.根据该样本匹配归入最近的中心：

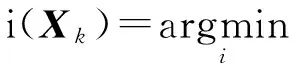
(12)

(13)

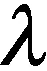
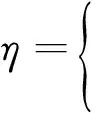
(14)

ΔMSE=MESi+1-MSEi,ψ≤-2

(15)

式中:γ初值为1;ψ是预置ΔMSE数量级阈值. 设γmax是预置迭代次数阈值，γmax大则能避免局部最优，反之，则易于收敛.如式(13)至(15)，迭代循环中，γ=γ+1;当ΔMSE<10ψ时，γ重置为初值．迭代次数集合为

(16)

理论上，聚类中心稳定，则k-均值算法收敛.实际中，设定一个较小的阈值θ，若聚类中心的变化小于此阈值，则停止计算;若结果未收敛，则转至式(12)循环迭代.k-均值算子运行结束时，得到ti(n)为最终聚类中心.各中心间最大距离

(17)

式中，i′,i″∈[1,I].

2.3 MAPSO优化参数

经过上述步骤得到各中心Ci和样本距中心的最大距离dmax.为取得权重ωij，文中采用MAPSO优化算法，依靠个体和全局最优更新粒子速度和位置．

设D维搜索空间种群为FT=(FT1,TT2,…，FTn)，此处n为T时段内采集次数，即样本数.第i个粒子为某一D维向量FTi=[Fi1,Fi2,…，FiD]T.按照目标函数φ(Xk,Ci)获取各粒子位置xi相应的适应度值.第i个粒子速度是Vi=[vi1,vi2,…，viD]T，个体极值是Pi=[Pi1,Pi2,…，PiD]T，种群全局极值是Pg=[Pg1,Pg2,…，PgD]T．

由于需要根据预定义的适应度函数求取各粒子适应度值，此处归一化求取适应度函数

(18)

式中,FT为空间中的某一样本，FTmin为样本最小值，FTmax为样本最大值，ε为样本FT中各维度元素值域的预设上限值．

已知PSO算法更新公式如下:

(19)

(20)

(21)

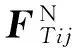
(22)

其中，

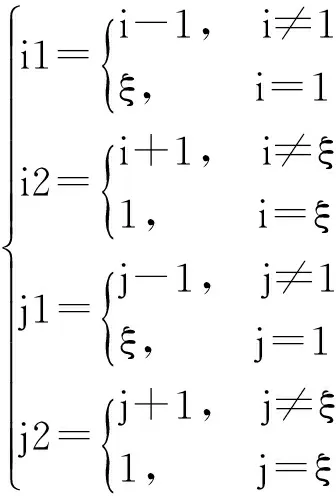
(23)

同时，各粒子实施固有的迭代更新，求最优解. 若更新后迭代次数达到kmax或阈值，则停止迭代取全局极值，否则跳转至式(18)，重新调整．

每次迭代后使用进化状态估计，调整MAPSO参数.文中采用自适应进化方法，在参数给定值域范围内，模糊调整这些参数值. 用N表示粒子群个数．

(24)

同理，求得个体间速率差异均值:

(25)

粒子飞行轨迹由位置和速度一起决定.通过式(26)和式(27)，建立混合dix与div的个体间轨迹差异均值dic，有

dic=dix+ρxivi*div

(26)

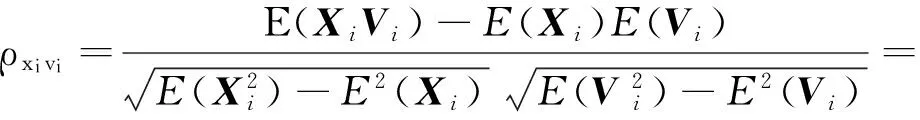
(27)

式中,E代表求和项，ρxivi为位置Xi和速度Vi的皮尔逊相关系数(PCC)．

比较全部dic，排序获得轨迹差异上限dcmax和下限dcmin.设dcg是全局最优粒子同各粒子间的轨迹差异均值,取轨迹差异均值进化因子ϑ．

(28)

将ϑ值采用模糊集映射函数分类．

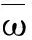
(29)

表1中的“微”调采用式(30)来定义．

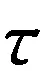
(30)

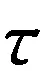
表1 加速系数1和2的调整策略

2.4 步骤流程

图3示出了KMP- RBF算法优化训练过程.文中提出的KMP- RBF融合算法简要步骤如下:

(1)建立RBF网络结构，明确关键参数．

(2)通过k- 均值算子和量子模糊改进的MAPSO算子优化RBF网络隐含层关键参数.

(3)以时间匹配训练数据，实施参数优化．

(4) 输入样本，在输出层后匹配空间，预测该路径行车时间．

图3 k- 均值和MAPSO优化的RBF网络流程

3 实验分析

3.1 实验设计

实地实车开展模型获取，调查时间为2016年3月2日起共35个工作日的每日交通最高峰1个小时，用线圈、车载GPS等方式对研究区域进行交通调查，实验路径为自某地某消防站至市博物馆，路线如图4所示，单程1.822 km.预调度一台实验用消防车，该车每5 min到达指定地点一次，后返回起点，循环往复.测得200组数据，其中前180组训练，用后20组预测文中方法的准确性．

图4 执勤行车实验路径及数据采集位置

全程分4个路段.设误差率阈值ε=3%，迭代次数上限为200.假设任何时候浮动车数量均高于下限.目标路径固定浮动车数最多为7 台，GPS采样时点相距时间为10 s.SCATS系统采用实验区域联机主控模式，由区域控制计算机自适应完成检测控制，最小绿灯时段10 s，可调采样时间间隔设为30 s.将SCATS与交通视频监控设备集成安装在各目标路段的出口停车线相应位置．

3.2 结果分析

3.2.1 误差率分析

如图5所示，不同类别监测系统在实测实验车辆行驶状态的对比误差率不同.使用车载GPS测得行车时间最高达到333.36 s，误差率达6.47%，且数据比较不稳定，这是因为GPS系统过度依赖同步卫星，易受干扰，定位出现延迟.SCATS系统对密集车流通过时的车头间距和车速监测结果存在较大差异，造成各路段的时点车流速度分布不均衡，相对误差也较大.而融合系统充分训练后明确了数据中心，输出误差最大为2.14%，预测时间较为稳定，变化趋势与实测数据更加接近．

如图6所示，在用不同算法预测所得的20组输出数据中，APSO- RBF和KMP- RBF算法误差率低，它基于量子模糊的参数自适应特征能够改善隐含层结构，拟合相关信息，较好地在交通峰值时段充分协调训练数据变化．

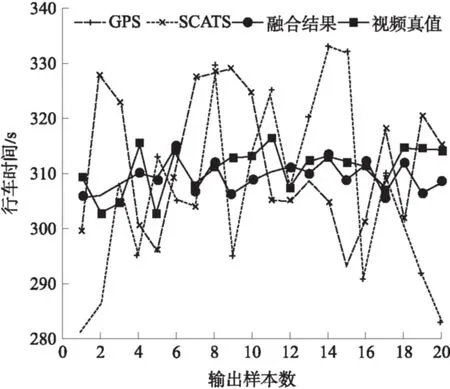
图5 融合输出行车时间对比

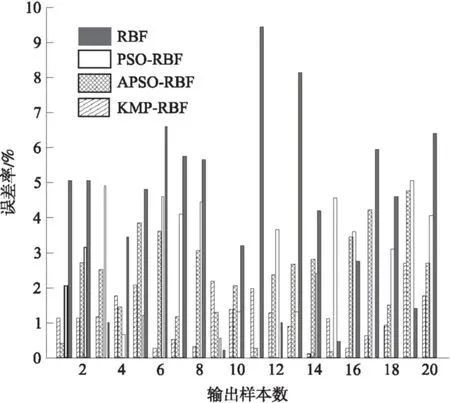
图6 相关算法误差率比较

将输出的行车时间引入均方差(MSE)、平均绝对误差(MAE)开展评价．

(31)

(32)

如表2所示， PSO- RBF算法[12]直接采用PSO更新RBF函数;APSO- RBF算法[13]在原有PSO- RBF 基础上进行改进，二者原理与文中算法均为对RBF函数优化，可作类比.其中，文中对KMP- RBF采用多智能体在系统构造过程中求得关键参数，引入聚类和模糊推理方法，减少了粒子维度，降低了陷入局部最优的可能性，其MSE与MAE较对比算法更为准确．

表2 相关算法误差数据分析

3.2.2 算法性能对比

算法迭代效率是影响收敛性的重要因素[14- 15].如图7所示，使用均方差MSE考察算法适应度水平，能够明确各类算法的细化程度和结果可靠性.其中，KMP- RBF在第18次迭代后趋于稳定，略晚于APSO- RBF的15次，但其细化寻优水平则较APSO- RBF、PSO- RBF超出10%以上.由于KMP- RBF算法对RBF网络的关键参数进行了多智能体的自适应调整，所以较其他算法能够获得更加精确的结果.但是其算法过程涉及k- 均值和模糊求取粒子群参数等多种迭代寻优，因此KMP- RBF并非最快收敛至稳定的算法．

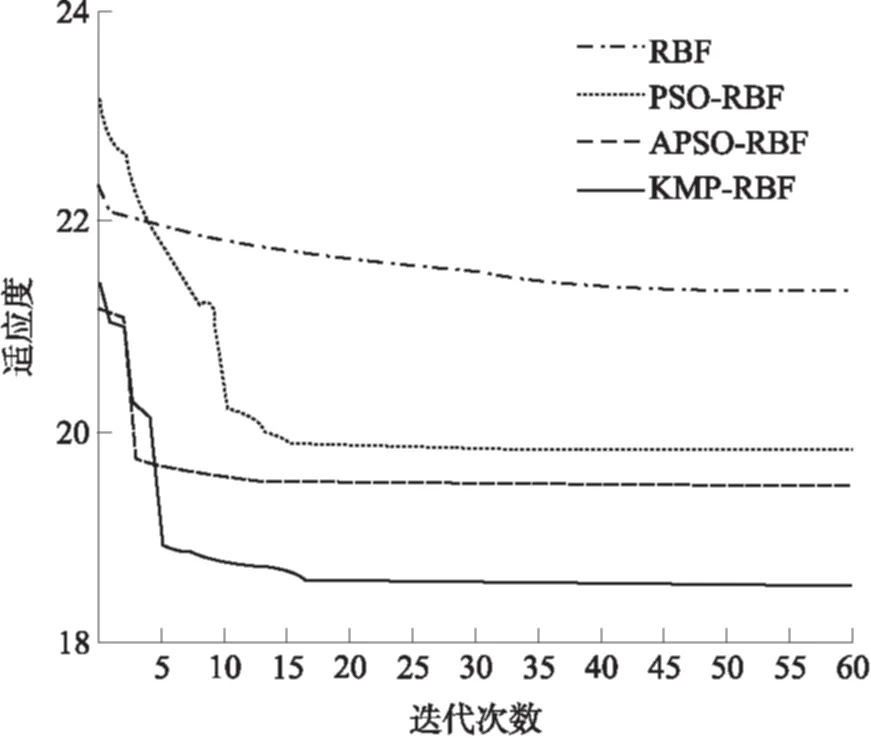
图7 相关算法适应度迭代比较

Fig.7 Adaptation iteration comparison among relevant algorithms

4 结论

文中提出的KMP- RBF算法是一种高效的自适应融合算法.该算法基于k- 均值聚类和模糊量子改进的MAPSO优化RBF网络隐含层关键参数，实现了网络与输入参数间的自适应，通过时间匹配、空间匹配分别实现输入、输出数据满足用户查询需求.实验对比证明，文中提出的算法具有较低的误差率和较高的精确度，适用于城市中执勤行车的路径选择．

[1] LIANG K，MARTENSSON J，JOHANSSON K H.Heavy- duty vehicle platoon formation for fuel efficiency [J].IEEE Transactions on Intelligent Transportation Systems，2016，17(4): 1051- 1061.

[2] 向郑涛，陈宇峰，李昱瑾，等.基于多尺度熵的交通流复杂性分析 [J].物理学报，2014，63(3):038903/1- 9. XIANG Zheng- tao，CHEN Yu- feng，LI Yu- jin，et al.Complexity analysis of traffic flow based on multi- scale entropy [J].Acta Physica Sinica，2014，63(3): 038903/1- 9.

[3] 李惠兵，杨晓光.面向行程时间预测准确度评价的数据融合方法 [J].同济大学学报(自然科学版)，2013，41(1):60- 65. LI Hui- bing，YANG Xiao- guang.Data fusion method for accuracy evaluation of travel time forecast [J].Journal of Tongji University (Natural Science)，2013，41(1): 60- 65.

[4] 杨兆升，莫祥伦，于尧，等.非常态下路段行程时间估计方法 [J].吉林大学学报(工学版)，2013，43(6):1459- 1465. YANG Zhao- sheng，MO Xiang- lun，YU Yao，et al.Estimation of travel time under abnormal state [J].Journal of Jilin University (Engineering and Technology Edition)，2013，43(6): 1459- 1465.

[5] 李清泉，胡波，乐阳.一种基于约束的最短路径低频浮动车数据地图匹配算法 [J].武汉大学学报(信息科学版)，2013，38(7):805- 808. LI Qing-quan，HU Bo，YUE Yang.Flowing car data map-matching based on constrained shortest path algorithm [J].Geomatic and Information Science of Wuhan University，2013，38(7): 805- 808.

[6] 李宇光，李清泉.利用地图栅格化的海量浮动车数据道路匹配快速算法 [J].武汉大学学报(信息科学版)，2014，39(6):724- 733. LI Yu- guang，LI Qing- quan.A fast algorithm for huge volume floating car data map- matching: a vector to raster map conversion approach [J].Geomatic and Information Science of Wuhan University，2014，39(6): 724- 733.

[7] MEHMET Y，NIKOLAS G.Experienced travel time prediction for congested freeways [J].Transportation Research (Part B): Methodological，2013，53: 45- 63.

[8] 赵建东，王浩，刘文辉.高速公路旅行时间的自适应插值卡尔曼滤波预测 [J].华南理工大学学报(自然科学版)，2014，42(2):109- 115. ZHAO Jian- dong，WANG Hao，LIU Wen- hui.Prediction of expressway travel time based on adaptive interpolation Kalman filtering [J].Journal of South China University of Technology (Natural Science Edition)，2014，42(2): 109- 115.

[9] 郑晓峰，王曙.基于粗糙集与关联规则的道路运输管理信息数据挖掘方法 [J].华南理工大学学报(自然科学版)，2014，42(2):132- 138. ZHENG Xiao- feng，WANG Shu.Data mining method of road transportation management information based on rough set and association rule [J].Journal of South China University of Technology (Natural Science Edition)，2014，42(2): 132- 138.

[10] LUOU S，MOHAMMED H.Practical approach for travel time estimation from point traffic detector data [J].Journal of Advanced Transportation，2013，47(5): 526- 535.

[11] HWANG K P，LEE W H，WU W B.Travel time prediction by weighted fusion of probing vehicles and vehicle detectors data sources [C]∥Proceedings of the 12th International Conference on ITS Telecommunications.Taipei: IEEE Communication Society，2012: 476- 481.

[12] KARAMI A，GUERRERO- ZAPATA M.A hybrid multiobjective RBF- PSO method for mitigating DoS attacks in named data networking [J].Neurocomputing，2014，151(11): 1262- 1282.

[13] ZHOU L K，LIU H Z.Operating parameter optimization of centrifuge based on APSO- RBF [C]∥Proceedings of 2011 International Conference on Transportation，Mechanical，and Electrical Engineering (TMEE).Changchun: IEEE，2011: 2111- 2114.

[14] 阎莹，王晓飞.灾变事件下高速公路管理单元的行程时间研究 [J].华南理工大学学报(自然科学版)，2015，43(12):99- 105． YAN Ying，WANG Xiao- fei.Investigation into travel time of management unit of expressway in disastrous events [J].Journal of South China University of Technology (Natural Science Edition)，2015，43(12):99- 105.

[15] 刘树青，徐建闽，卢凯，等.用于交通流预测的带距离权重模式识别算法 [J].华南理工大学学报(自然科学版)，2015，43(12):114- 126． LIU Shu-qing，XU Jian-min，LU Kai，et al.A distance-based weighted pattern recognition algorithm for traffic flow forecasting [J].Journal of South China University of Technology (Natural Science Edition)，2015，43(12): 114- 126.

A KMP- RBF Fusion Method to Forecast Duty Vehicle’s Travel Time

JINShan1，2JINZhi-gang1LIUYong-lei1

(1.School of Electrical and Information Engineering,Tianjin University,Tianjin 300072,China;2.Fire Department of Tianjin, Tianjin 300020, China)

Proposed in this paper is a KMP- RBF fusion method for forecasting the travel time of duty vehicle.In this method, the signal source consisting of GPS information and SCATS (Sydney Coordinated Adaptive Traffic System) is utilized to establish a traffic information fusion model that combines fuzzy inference knowledge representation, MAPSO (Multi- Agent Particle Swarm Optimization) and RBF (Radial Basis Function) training together, the key parameters are optimized adaptively, and the time and space data are matched and obtained from historical training database.Experimental results show that the travel time after fusion and prediction is identical to the actual data measured by the traffic monitoring system, and that the proposed KMP- RBF fusion method is effective and reliable in the aspects of error rate, iterative degree and accuracy.

information fusion; forecasting; fuzzy inference; multi- agent particle swarm optimization algorithm; RBF networks;k- means algorithm; duty vehicle’s travel time

2016- 05- 06

国家自然科学基金资助项目(61201179); 国家博士后科学基金资助项目(2016M601265) Foundation items: Supported by the National Natural Science Foundation of China (61201179) and the National Postdoctoral Foundation(2016M601265)

金杉(1982-)，男，博士生,工程师,主要从事通信系统及工程、人工智能、无线传感器网络研究.E-mail:shanye2006@163.com

1000- 565X(2017)03- 0035- 07

TP 202

10.3969/j.issn.1000-565X.2017.03.005