CVS中基于残差结构特征的块分类重构算法*
2017-06-21杨春玲李文豪
杨春玲 李文豪
(华南理工大学 电子信息学院, 广东 广州 510640)
CVS中基于残差结构特征的块分类重构算法*
杨春玲 李文豪
(华南理工大学 电子信息学院, 广东 广州 510640)
现有最好的视频压缩感知重构算法大都采用“预测-残差重构”策略,可有效利用帧内和帧间的相关性获得较好的性能,但是残差重构均直接采用SPL算法,忽略了残差信号自身的结构特征,限制了性能的进一步提升.针对该问题,文中提出了一种基于预测残差结构特征的块分类重构算法,首先利用残差块观测值的平均能量对残差块进行分类,然后对不同类的残差块采用不同的重构算法.仿真实验表明,用于运动较快的视频序列时,文中方案与SPL算法相比可以获得更好的重构质量.
视频压缩感知;残差重构;平均能量;残差块分类
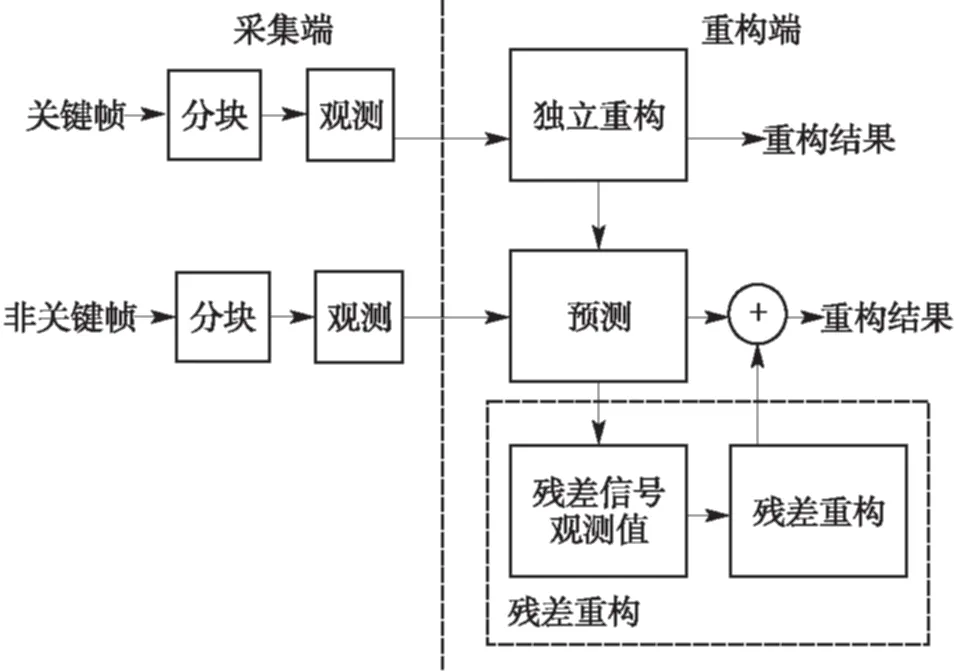
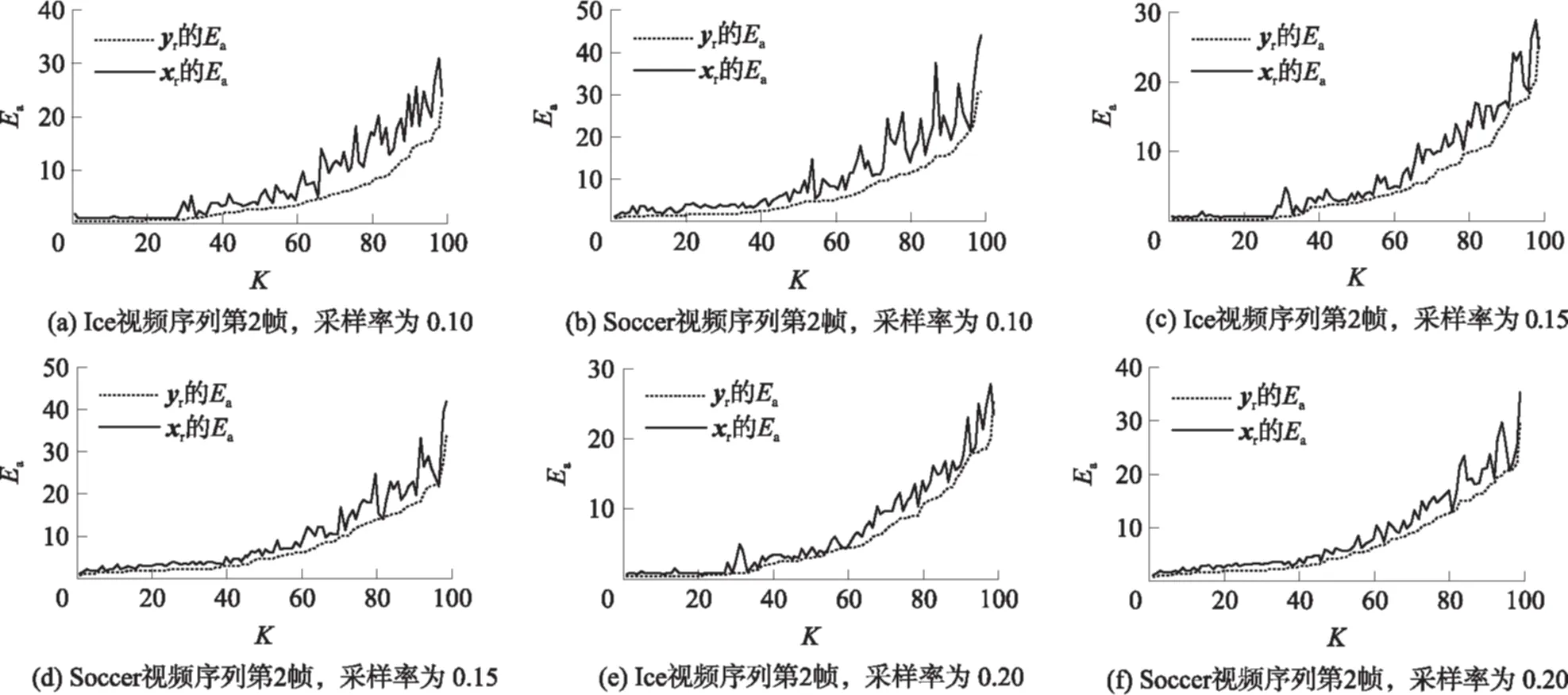
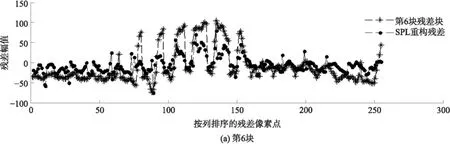
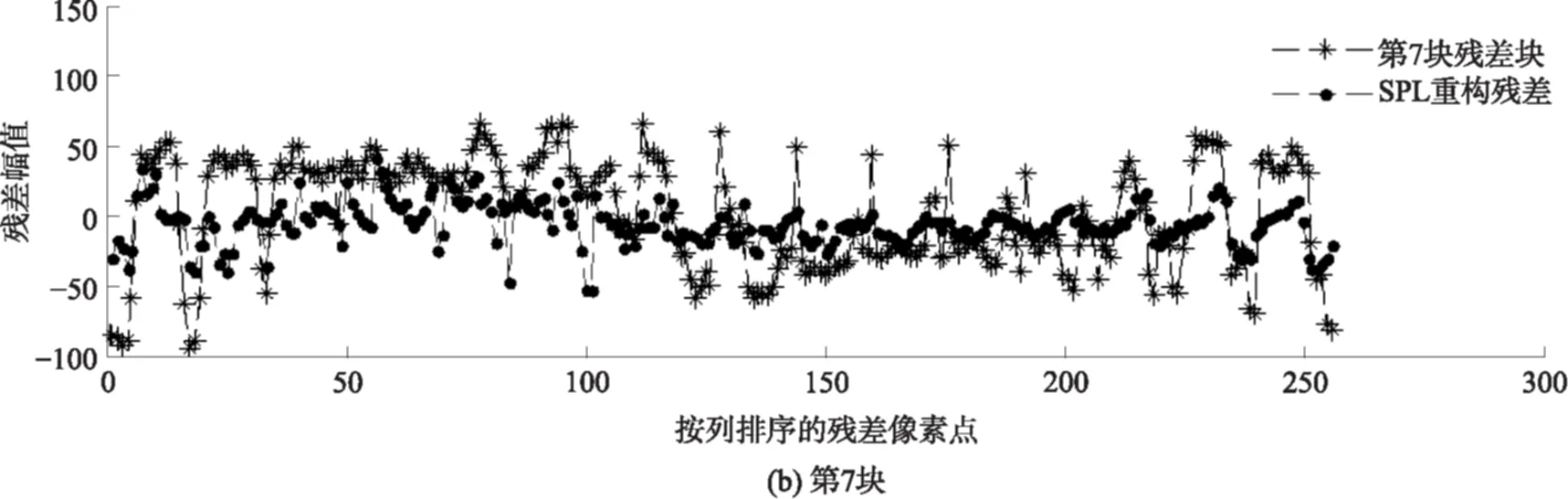
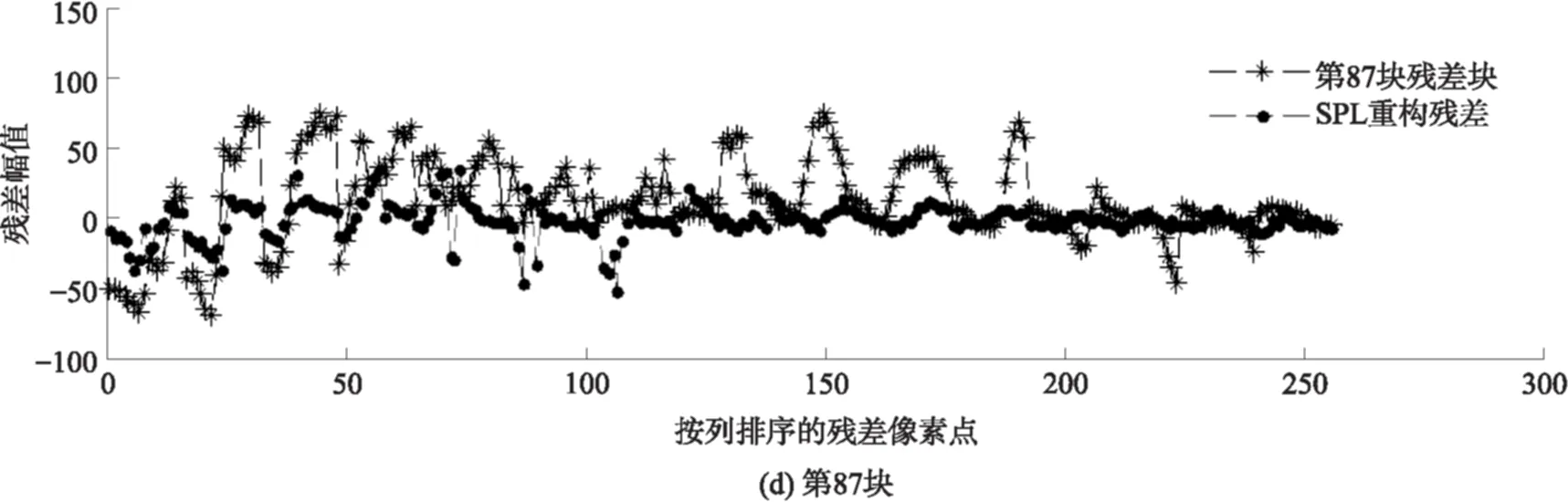
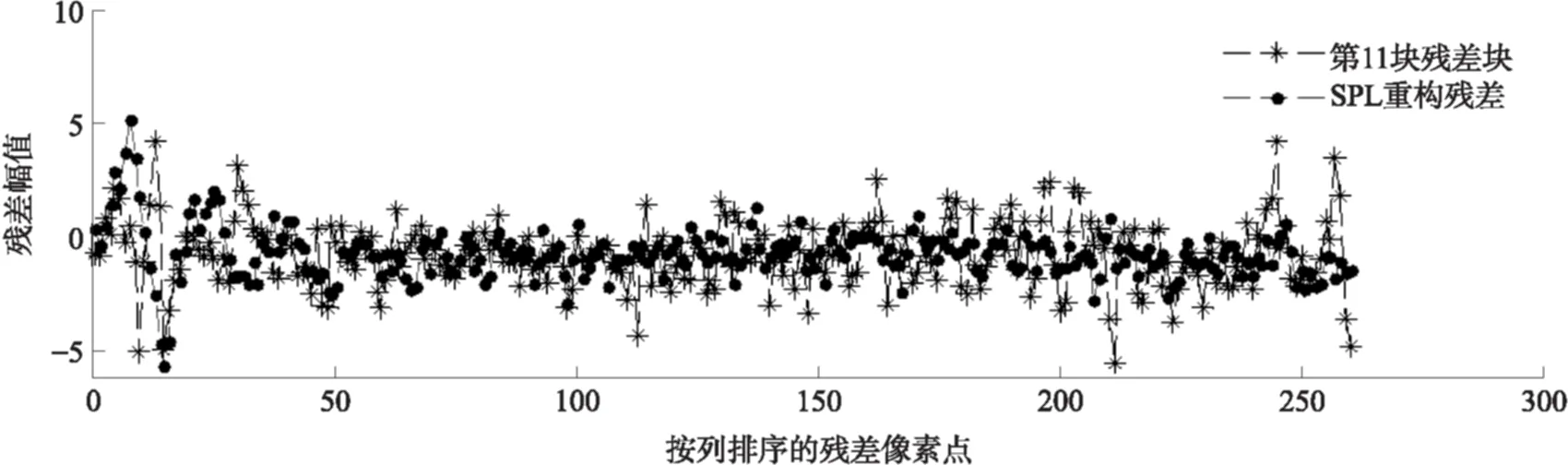
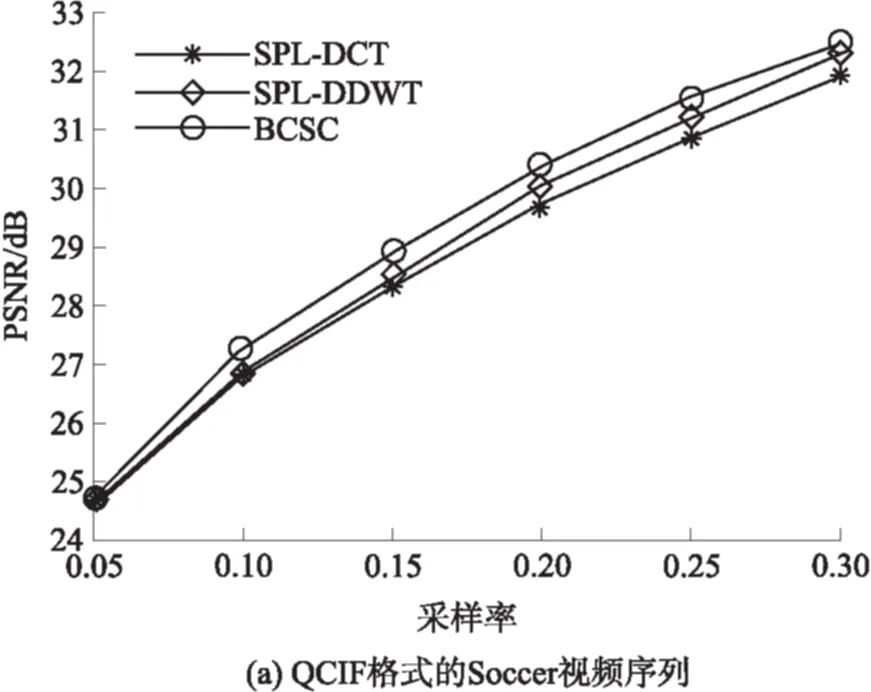
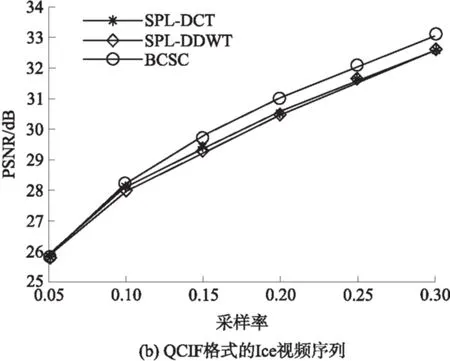
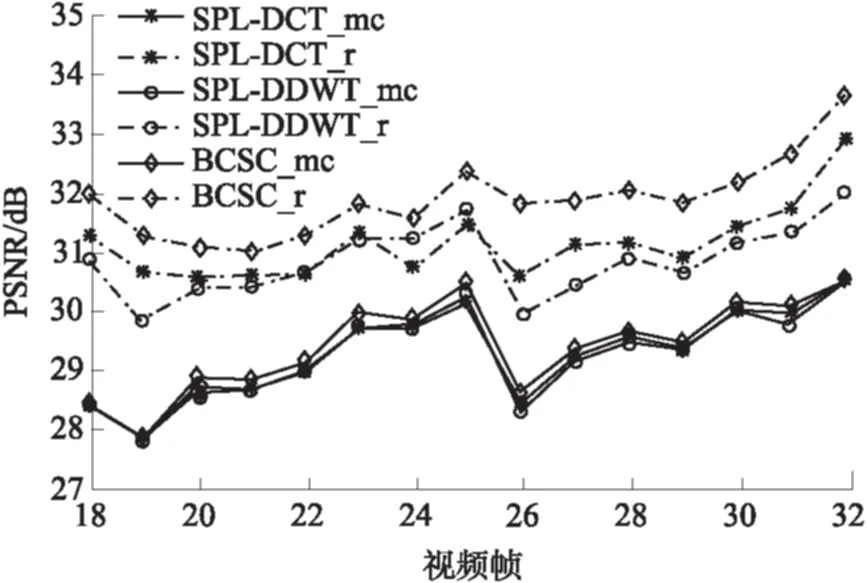
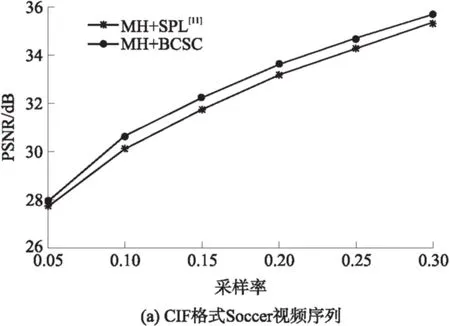
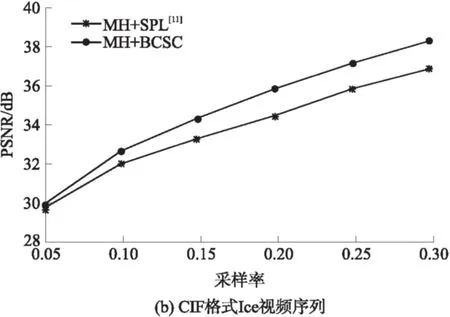
近十年来,压缩感知理论在信号处理领域受到极大的关注,该理论指出:对于在某个变换域ψ下稀疏或近似稀疏的N维信号,可以通过它的M(M 将压缩感知理论应用于图像信号采集被称之为图像压缩感知,文献[3]使用分块压缩感知(BCS)方法对图像进行分块观测和处理,具有快速高效的优点,是目前最受关注的图像压缩感知框架;在此框架基础上,文献[4]进一步提出结合平滑处理和迭代Landweber投影的BCS-SPL重构算法,该算法能够很好地权衡计算复杂度和重构质量,是目前图像压缩感知中比较被认可的重构算法,由于它的快速和高效,亦被广泛应用于视频压缩感知的残差重构中. 将压缩感知理论应用于视频信号的采集和处理被称之为视频压缩感知(CVS),视频压缩感知算法虽然可以采取逐帧独立重构、立体重构[5]以及帧差重构[6- 7]等多种策略[8],但是都不如“预测-残差重构”策略,它能够更好地利用帧内和帧间的相关性,因此现有重构质量最好的视频压缩感知算法都基于该框架进行[9- 12].由于视频信号不仅具有帧内相关性而且还具有帧间相关性,而逐帧独立重构是将视频信号的每一帧单独处理,忽略了帧间相关性,导致重构质量很差;立体重构利用时域相关性辅助选取或设计合适的稀疏变换,从而提升重构质量,该思路中比较有代表性的是文献[5],其利用帧间相关性构造自适应的局部KLT变换基以获得比单一固定稀疏基更好的稀疏性,但是该方法计算复杂度较高;帧差重构是利用帧间相关性对更稀疏的帧差进行重构,文献[6]利用帧差的聚类稀疏性对帧差进行二值化下的膨胀和腐蚀等操作,能够有效去除噪声并恢复损失的帧差信息,但是帧差都来自于关键帧和非关键帧之差,导致在大GOP条件下或对于帧间相关性变差的运动较快的序列,重构质量下降;文献[7]提出基于帧差空域稀疏性的最小总变分(TV)重构方案,虽然帧差来自于相邻两帧,较文献[6]有所改进,但是只对帧间变化极小的视频序列有作用. 预测-残差重构作为一种分布式视频压缩感知框架,其主要研究非关键帧的重构方法,它首先利用帧间相关性对当前非关键帧进行预测,然后再对预测后的残差进行重构,是目前性能最好的视频压缩感知重构方案.现有的视频压缩感知重构算法大都只关注如何提高预测精度[9- 15],而忽略了作为该策略重要组成部分的残差重构.文献[13]首先提出利用最小平方问题求解的像素域多假设(MH)预测模型;文献[14]进一步提出添加Tikhonov约束的观测域多假设预测模型,该模型使预测更加准确;文献[15]使用多假设预测系数稀疏的约束替换Tikhonov约束,但是该假定在某些情况下会导致预测质量下降.为了进一步提高预测精度,文献[9]提出混合预测方案,对图像块进行筛选并使用不同预测模型进行预测;在该方案基础上文献[10]添加假设集筛选和更新等步骤来优化假设块集合;同时文献[11]提出多参考帧的假设集优化方案以进一步利用帧间相关性,文献[12]又提出两阶段的观测域-像素域多假设预测方案,可以有效提高预测精度和去除块效应.文献[9- 15]均直接采用适合于自然图像压缩感知的BCS-SPL重构算法进行残差重构,忽视了残差信号自身的结构特征,导致残差重构对最终性能的贡献不大. 残差重构作为“预测-残差重构”的重要组成部分,对最终重构质量有着至关重要的影响,但基于该框架的残差重构都是采用SPL重构算法[4].而SPL重构算法是一种图像压缩感知的重构算法,适合于图像的结构特征,视频预测残差信号不再具有自然图像的结构特征,因此用SPL重构算法对预测残差进行重构性能不佳.针对该问题,文中深入研究残差信号的结构特征和不同结构特征残差块所对应的最优重构算法,提出了一种基于预测残差信号结构特征的块分类重构算法(BCSC),可应用于运动较快的视频序列,以提升重构质量.在BCSC算法中,首先根据残差块观测值的平均能量对残差块分类,然后对各类残差块采用相应的重构算法进行残差重构. 1.1 “预测-残差重构”框架 现有重构质量最好的视频压缩感知算法都是基于“预测-残差重构”框架,该框架具体如图1所示,其中关键帧采用MH-BCS-SPL算法[16]进行独立重构,非关键帧通过预测和残差重构得到. 在该框架下,预测精度会影响残差重构的质量,反过来残差重构也会影响下一步或下一帧的预测精度,可见残差重构质量对视频压缩感知的重构性能影响较大.目前广泛用于该框架的残差重构算法是BCS-SPL图像压缩感知重构算法. 图1 “预测-残差重构”框架 1.2 BCS-SPL算法 图像压缩感知的BCS-SPL算法由于其高效快速的优点,也被用在视频压缩感知的残差重构,算法框图如图2所示[4]. 图2 BCS-SPL算法框图 其中维纳滤波用来消除块效应,而凸投影(文献[4]中的Landweber投影)的表达式为 (1) (2) 在该算法中,虽然可以选择Contourlet变换(CT)、离散小波变换(DWT)、离散余弦变换(DCT)和双树离散小波变换(DDWT)等不同的稀疏基[4], 且基于DCT或DDWT稀疏基的BCS-SPL算法常用于残差重构,但是由于残差信号不再具有自然图像的结构特征,不同残差块具有不同的结构特征,因此选择单一稀疏基或同一种重构方法都不够合理. 首先从理论上分析多假设预测后的残差观测值和残差信号之间的平均能量关系,并进行仿真验证,然后从平均能量的角度对残差块的特征进行分析并探究BCS-SPL算法的缺点,最后提出基于平均能量的残差块分类标准以及适用各类残差块特征的重构方案. 2.1 观测值和残差信号平均能量的关系特征 由于运动较快的视频序列帧间变化很大,在多假设预测模型下,对包含不同快慢运动的图像块进行预测得到的残差信号具有不同的特征:运动较慢的背景区域因为具有较强帧间相关性,所以预测比较准确;而运动较快的过渡区域以及运动物体由于帧间相关性较弱,所以预测质量相对较差. 观测矩阵φ采用随机高斯矩阵时,它的每个元素φi,j相互独立且均服从正态N(0,σ2)分布,对于N维残差信号xr,其M维观测值yr满足式(2),对于yr中的第i个元素, (3) (4) (5) (6) 由以上的推导可知,利用随机高斯观测矩阵得到的残差观测值yr的平均能量Ea和残差信号xr的平均能量整体上呈正比关系. 利用实际视频信号验证残差观测值yr的平均能量和残差信号xr的平均能量之间的关系,仿真实验结果见图3.分别对QCIP的Soccer和Ice标准视频序列的前两帧进行处理,第1帧为关键帧,采样率为0.70,采用MH-BCS-SPL算法[16]进行独立重构,第2帧利用文献[12]中的第1阶段多假设预测模型进行预测,然后对预测残差信号xr和yr残差观测值平均能量进行统计.其中分块大小均为16,采样率分别为0.10、0.15和0.20,分别对应图3中(a)-(f),图中横坐标K表示残差块按它的yr平均能量排列后的残差块序号. 从图3的实验结果可以看出,残差观测值yr和xr残差信号的平均能量整体上确实呈正比关系. 图3 观测值yr和残差信号xr平均能量的关系 2.2 残差块结构特征分析 对于商务英语专业的学生来说,确定一个研究方向,选取有价值的问题进行分析论述,认真完成毕业论文是必要的。毕业论文字数在3 000~5 000词左右,要求能够用英语对实际论点进行论证,并且有一定的创新性。鼓励学生采用商务报告的形式,例如商业计划书、营销方案等进行写作。 由上述分析可知,一般情况下,大能量残差块的观测值能量也较大,小能量残差快的观测值能量也较小.笔者深入研究发现,不同能量的残差块结构特征非常不同. 2.2.1 较大能量残差块的特征分析 研究中发现,平均能量较大的预测残差块对应的图像块往往属于运动物体和背景的过渡区域,而这些区域的图像块具有分段平滑的特性.图4中给出了Soccer标准视频序列第2帧的原始图像、预测图像和重构图像的视觉效果图,并在图中标记了3个预测残差能量较大的区域A、B、C,从图4中可以看出,采用SPL算法进行残差重构后的图像会丢失边缘细节信息(对应区域A),或引入一些高频噪声(对应区域B和C). 图4 Soccer视频序列第2帧视觉效果Fig.4 Visual effect of the second frame of Soccer video sequence 为进一步分析这些图像块所具有的结构特征以及SPL算法不适用这些残差块的原因,图5中放大了图4中标记区域的图像块,分别为第6、7、24和87块,它们在0.15采样率下的平均能量分别为41.64、39.31、23.73和33.05,并给出得到的预测块、残差块、使用重构算法进行残差重构得到的残差块和最终结果;同时在图6中给出这些残差块和使用SPL重构算法进行残差重构得到的残差块的幅值分布图.从图5和图6中可以明显看出,这些图像块具有分段平滑的特性,其预测块也具有一定的分段平滑性,残差块也是分段平滑的.图5中还可以看出,采用SPL算法进行重构的残差块不再具有很好的分段平滑性;同时从最终结果可以看出,第7块中运动物体的轮廓很不清晰,而其他块的背景部分也引入了高频噪声.这是因为采用SPL重构算法对残差进行重构,存在两个明显的问题:一是维纳滤波虽然可以去除残差块与块之间的块效应,但会弱化残差块内的边缘信息,模糊掉分段平滑图像块的边缘,这个结果是比较致命的;二是,SPL算法是一种迭代重构算法,在初始重构中会引入高频噪声,对于平均能量较大的残差块,初始重构噪声比较大,对DDWT作为稀疏基的不同频带分别进行阈值处理时,初始重构引入的大能量残差块的高频噪声很难通过阈值处理有效消除. 图5 较大能量残差块的结构特征 由以上分析可见,能量较大的残差块采用SPL重构算法重构性能很差,需要探究合适其结构特征的重构算法,该问题在下一小节有详细的研究. 2.2.2 较小能量残差块的特征分析 平均能量较小的残差块对应的预测图像块比较准确,采用SPL算法对这类残差块的重构性能也不好.这是由于这类残差块一般只有个别像素的幅度值比较大,而其他像素的幅度值都接近于0,因此该类残差块在空间域具有一定的稀疏性,在变换域就不具有稀疏性了,采用SPL算法进行残差重构不适合这类残差块特征.图7给出了Soccer标准视频序列第2帧第11个残差块(平均能量为1.50)的幅值分布图及SPL重构信息的分布.由图7可见,该残差块只有极个别幅值较大,整体幅值分布在0附近,表明它在空间域具有一定的稀疏性.SPL重构中不仅没有重构出大幅值点,而且重构结果还引入了噪声.因此这类图像块采用空间域的压缩感知重构算法会有更好的重构效果. 2.3 残差块分类及分类残差重构方案 根据上述分析可知,残差观测值yr和残差信号 xr的平均能量大小整体呈正比关系,而且不同平均能量大小的观测值yr对应的残差信号又具有不同特征.对于观测值yr平均能量较大的残差块往往具有分段平滑特性,而采用BCS-SPL算法重构会丢失残差块中的边缘细节信息并且对背景引入高频噪声,因此重构方法应该确保残差重构的结果也具有分段平滑的特性.对于m×n维的残差块xr,它的总变分定义为 (7) 根据该定义可知,基于总变分最小的重构算法可以降低相邻像素之间的变化剧烈程度,因此该类算法对本身具有分段平滑特性的信号有很好的重构性能[17- 19],所以文中提出利用求解残差信号总变分最小化对这类残差块进行重构,并使用文献[20]中的对数障碍法求解该优化问题. (8) s.t.‖φ xr-yr‖2≤ε. 式中,ε为阈值. 对于观测值yr平均能量较小的残差块,因为对应的预测块已比较准确,该类残差块中往往只有较少的大值,而其他像素点的幅值都接近于0,在空域有一定的稀疏性,在变换域就不具有稀疏性了,所以文中提出利用像素域稀疏信号重构方法对该类残差块进行重构.较好的像素域重构算法有IHT[21]、FIHT[22]、CoSaMP[23]以及CGIHT[24- 25].其中CGIHT算法在IHT算法与FIHT算法的基础上引入共轭梯度,从而在一定时间复杂度下有效提升了算法的收敛速度,同时在低采样率下具有比CoSaMP算法更好的重构质量,因此最终选择CGIHT算法重构这类残差块. 基于以上分析,文中提出基于残差观测值yr平均能量的残差块分类标准,并提出适应各类残差块特征的重构方案,具体如图8所示,其中变量t1和t2为划分残差块类型的阈值. 在该方案中,阈值t1和t2的选择会影响到最终重构质量,因为预测精度会影响所有残差块的平均能量,同时残差块的结构特征又和平均能量的绝对大小有关,所以在文中通过大量的仿真实验及分析选择固定的阈值进行残差块分类. 图6 较大能量残差块的幅值分布图 图7 Soccer视频序列第2帧第11个残差块的幅值分布图 图8 残差块分类标准和重构方案 Fig.8 Classifying criterion and reconstruction scheme of resi-dual blocks 利用本文提出的重构算法分别对QCIF(176×144)格式和CIF(352×288)格式的视频序列做了仿真实验.下面分别对这两部分仿真实验结果进行分析讨论. 3.1 对QCIF格式视频序列的实验结果分析 由图9可以看出,文中提出的BCSC重构方案的重构质量均好于SPL的结果.其对于Soccer视频序列最大的性能增益为0.65 dB(对应采样率为0.25),对于Ice视频序列最大的增益为0.58 dB(对应采样率为0.20).所提算法重构性能的提升主要得益于观测值yr平均能量较大的残差块的准确重构,因为这些残差块具有分段平滑性,所以在TV下更稀疏,而观测值yr平均能量较小的残差块重构性能提升不大,这是因为对应的图像块预测比较准确.另外,由图9可见,随着采样率增大所提算法的增益先上升后下降,这是因为在采样率极低的情况下残差观测值的信息较少,重构性能难以提升,而在采样率较高的情况下由于预测结果更加准确所以通过残差重构能够进一步提升的性能也受到了限制. 图9 SPL和BCSC的PSNR对比 从图9中还可以看出,两个标准视频序列在不同的稀疏基下进行残差重构时质量不同,且Soccer视频序列在DDWT变换域得到更好的重构效果,而Ice视频序列在DCT域得到的重构效果更好.这和预测图像的特征以及不同稀疏基的阈值处理方式有关:Soccer视频序列预测残差的块效应较少,在DDWT表示信号更加稀疏,因此取得了较好的重构效果;而Ice视频序列块效应较多,DDWT的稀疏性不好,因此重构效果不如DCT域的重构效果好. 然后,进一步给出Ice视频序列在0.25采样率下第2个GOP非关键帧的PSNR对比图,如图10所示.其中“_mc”和“_r”分别为运动估计和残差重构得到的结果. 图10 QCIF格式Ice视频序列在0.25采样率下第2个GOP非关键帧的PSNR对比 Fig.10 Comparison of PSNR of the 2nd GOP of Ice video sequence at a sampling rate of 0.25 由图10可见,文中提出的BCSC重构算法可以得到更好的重构结果,而且预测性能也有所提升.这是因为采用多参考帧的方式进行预测[12],预测和残差重构的质量相互影响,在第18帧以及第32帧预测结果相同的情况下,使用文中方案进行残差重构能够更好地提升性能,这使得第19帧以及第31帧在更精确的参考帧上进行预测,因此它们的预测结果也最好. 图11给出了Ice视频序列在0.25采样率下第26帧的视觉效果图,图11(b)和(c)为分别采用基于DCT和DDWT的BCS-SPL算法进行残差重构的最终结果(30.55 dB和29.89 dB),图11(d)为采用文中方案进行残差重构的最终结果(31.84 dB).从图11中所标记的D和E两个区域可明显看出,采用文中提出的BCSC方案进行残差重构可以获得比SPL算法更好的视觉效果.从区域D可以看出,采用BCSC方案并没有在背景中引入高频噪声,从区域E可以看出,采用BCSC方案很好地保留了图像中的边缘信息. 图11 QCIF格式Ice视频序列在0.25采样率下第26帧视觉效果对比 Fig.11 Comparison of visual effect of the 26th frame of Ice video sequence at a sampling rate of 0.25 3.2 对CIF格式视频序列的实验结果分析 对CIF格式的Soccer和Ice标准视频序列的前289帧和前225帧分别进行仿真实验,非关键帧的平均PSNR结果见图12,并和文献[11]的仿真结果进行了对比.仿真实验中文献[11]采用基于DDWT的BCS-SPL算法进行残差重构,文中采用BCSC算法进行残差重构,其他实验条件完全相同:GOP大小为16,关键帧采样率为0.70,并采用MH-BCS-SPL[16]算法进行独立重构,非关键帧采用观测域多假设预测模型进行预测[11- 12]. 图12 CIF格式视频序列的PSNR对比 从实验结果可以看出,在实验条件完全相同的情况下,残差重构采用BCSC方案,要明显优于SPL方案.PSNR最大增益为1.45 dB,这是因为对于运动较快的视频序列BCSC可以有效去除高频噪声或保留图像的边缘信息. 针对大多数采用“预测-残差重构”策略的视频压缩感知算法忽略残差信号特征的问题,文中首先从理论上分析了残差信号和残差观测值的平均能量的关系,并对不同平均能量的残差块的结构特征进行了深入分析,然后提出了基于观测值平均能量的残差块分类方法和残差块分类重构算法(BCSC).本文提出的BCSC残差重构算法用于运动较快的视频序列,可以有效解决直接采用SPL算法丢失边缘信息和对背景引入高频噪声的问题,提升视频信号的重构质量.在该研究思路下需进一步对残差信号更合理的分类方法和基于不同预测模型得到的残差信号所具有的空间特征等开展深入的研究. [1] 石光明,刘丹华,高大化,等.压缩感知理论及其研究进展 [J].电子学报,2009,37(5):1070- 1081. SHI Guang- ming,LIU Dan- hua,GAO Da- hua,et al. Advances in theory and application of compressed sensing [J]. Acta Electronica Sinica,2009,37(5):1070- 1081. [2] QAISAR S,BILAL R M,IQBAIL W,et al. Compressive sensing:from theory to application,a survey [J]. Journal of Communications and Networks,2013,15(5):443- 456. [3] GAN Lu. Block compressed sensing of natural images[C]∥ Proceedings of 2007 15th International Conference on IEEE Digital Signal Processing. Cardiff:IEEE,2007:403- 406. [4] MUN S,FOWLER J E. Block compressed sensing of images using directional transforms[C]∥Proceedings of 2009 16th International Conference on IEEE Image Processing(ICIP). Cairo:IEEE,2009:3021- 3024. [5] LIU YING,LI MING,PADOS D A. Motion- aware decoding of compressed- sensed video [J].IEEE Transactions on Circuits and System for Video Technology,2013,23(3):438- 444. [6] WANG S,SHAHRASHI B,RAHNAVARD N. SRL1:structured reweighted l1 minimization for compressive sampling of videos[C]∥Proceedings of IEEE International Symposium on Information Theory Proceedings (ISIT).Istanbul:IEEE,2013:301- 305. [7] ZHENG Jing,JACOBS E L. Video compressive sensing using spatial domain sparsity [J]. Optical Engineering,2009,48(8):1- 10. [8] 李然,干宗良,崔子冠,等. 联合时空特征的视频分块压缩感知重构 [J]. 电子与信息学报,2014,36(2):285- 292. LI Ran,GAN Zong- liang,CUI Zi- guan,et al. Block compressed sensing reconstruction of video combined with temporal- spatial characteristic [J]. Journal of Electronics and Information Technology,2014,36(2):285- 292. [9] CHEN Jian,CHEN Yunzheng,QIN Dong,et al. An elastic net-based hybrid hypothesis method for compressed video sensing [J]. Multimedia Tools and Applications,2013,74(6):2085- 2108. [10] KUO Y,CHEN Jian. A scheme for distributed compressed video sensing based on hypothesis set optimization techniques [J]. Multidimensional Systems and Signal Processing,2017,28(1):129- 148. [11] 杨春玲,欧伟枫. CVS中基于多参考帧的最优假设预测算法 [J]. 华南理工大学学报(自然科学版),2016,44(1):1- 8. YANG Chun- ling,OU Wei- feng.Multi- reference frames- based optimal multi- hypothesis prediction algorithm for compressed video sensing [J]. Journal of South China University of Technology(Natural Science Edition),2016,44(1):1- 8. [12] OU Weifeng,YANG Chunling,LI Wenhao,et al. A two- stage multi-hypothesis reconstruction scheme in compressed video sensing [C]∥Proceedings of ICIP2016. Phoenix:IEEE,2016:2494- 2498. [13] MUN S,FOWLER J E. Residual reconstruction for block- based compressed sensing of video[C]∥Proceedings of Data Compression Conference.Snowbird:IEEE,2011:183- 192. [14] TRAMEL E W,FOWLER J E. Video compressed sen-sing with multihypothesis[C]∥Proceedings of Data Compression Conference.Snowbird:IEEE,2011:193- 202. [15] DO T T,CHEN YI,NGUYEN D T,et al. Distributed compressed video sensing[C]∥Proceedings of IEEE Conference on Image Processing.Cairo:IEEE,2009:1393- 1396. [16] CHEN Chen,TRAMEL E W,FOWLER J E. Compressed- sensing recovery of images and video using multihtpothesis predictions[C]∥Proceedings of Asilomar Conference on SSCPG.Pacific Grove:IEEE,2011:1193- 1198. [17] ZHANG Jian,LIU Shaohui,ZHAO Debin. Improved total variation based image compressive sensing recovery by nonlocal regularization[C]∥Proceedings of IEEE International Symposium on Circuit and Systems. Beijing:IEEE,2013:2836- 2839. [18] DONG W,YANG X,SHI G. Compressive sensing via reweighted TV and nonlocal sparsity regularization [J]. IET Electronics Letters,2013,49(3):184- 186. [19] CANH T N,DINH K Q,JEON B. Total variation reconstruction for Kronecker compressive sensing with a new regularization[C]∥Proceedings of Picture Coding Symposium (PCS). San Jose:IEEE,2013:261- 264. [20] CANDES E,ROMBERG J. l1- magic:recovery of sparse signals via convex programming[EB/OL]. (2016- 03- 13)[2016- 05- 10].www.acm.caltech.edu/llmagic/downloads/llmagic. [21] BLUMENSATH T,DAVIES M E.Iterative hard thresholding for compressed sensing [J].Applied Computational Harmonic Analysis,2009,27(3):265- 274. [22] WEIKe. Fast iterative hard thresholding for compressed sensing [J]. IEEE Signal Processing Letters,2015,22(5):593- 597. [23] NEEDELL D,TROPP J A. CoSaMP:iterative signal recovery from incomplete and inaccurate samples [J].Applied Computational Harmonic Analysis,2009,26(3):301- 321. [24] BLANCHARD J D,TANNER J,Wei K. CGIHT:conjugate gradient iterative hard thresholding for compressed sensing and matrix completion [J]. Information and Inference,2015,4(4):289- 327. [25] BLANCHARD J D,TANNER J,WEI K. Conjugate gradient iterative hardthresholding:observed noise stability for compressed sensing [J].IEEE Transactions on Signal Processing,2015,63(2):528- 537. Residual Structure Characteristics-Based Block Classifying Reconstruction Algorithm for CVS YANGChun-lingLIWen-hao (School of Electronic and Information Engineering, South China University of Technology, Guangzhou 510640, Guangdong, China) Most existing compressed video sensing (CVS) algorithms with best reconstruction performance adopt a“prediction-residual reconstruction”strategy, which helps obtain high reconstruction quality by taking good advantage of intra-frame and inter-frame correlation. However, all of them ignore the residual structure characteristics and simply use SPL reconstruction algorithm which is only suitable for natural image compressed sensing. In order to solve this problem, a block classifying reconstruction algorithm on the basis of residual structure characteristics is proposed, which firstly classifies residual blocks according to their average energy and then adopts suitable algorithms to reconstruct residual blocks corresponding to their structure characteristics. Simulated results show that the proposed algorithm helps achieve higher reconstruction quality than SPL algorithm for video sequences with fast movements. compressed video sensing; residual reconstruction; average energy; residual block classification 2016- 05- 25 广东省自然科学基金资助项目(2016A030313455) Foundation item: Supported by the Natural Science Foundation of Guangdong Province of China(2016A030313455) 杨春玲(1970-),女,博士,教授,主要从事图像/视频压缩感知研究.E-mail:eeclyang@scut.edu.cn 1000- 565X(2017)03- 0001- 10 TN 919.8 10.3969/j.issn.1000-565X.2017.03.0011 预测-残差重构与BCS-SPL算法


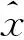
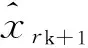
2 基于残差结构特征的重构算法
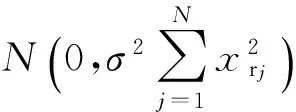




3 仿真结果与分析


4 结语
