论高考中常见的线性规划问题

山东省广饶职业中等专业学校 刘泽峰

一、基本类型

线性目标函数最值问题——直线的截距型（或截距的相反数）。

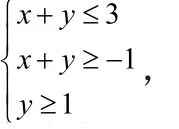
A.12 B.10 C.8 D.2

[答案] B

[解析] 画出可域如图中阴影部分所示，目标函数z＝4x＋2y可转化为

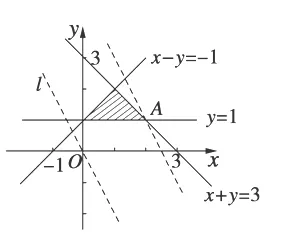
作出直线y＝－2x并平移，显然当其过点A时纵截距最大.

规律方法：

利用线性规划求最值。

1.准确画出可行域是解答此类问题的前提条件。

2.把目标函数值与过可行域内点的一组平行直线建立对应关系。

3.理解好线性目标函数的几何意义是关键。

最优解一般在可行域的边界上，并且通常在可行域的顶点处取得，所以作图时要力求准确。

非线性目标函数最值问题：

1.直线的斜率型

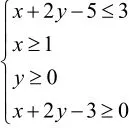
A.最大值是2，最小值是1

B.最大值是1，最小值是0

C.最大值是2，最小值是0

D.有最大值无最小值

[答案] C

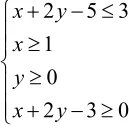
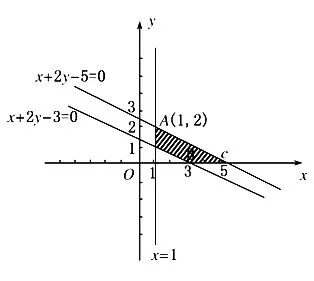
表示可行域内点与原点连线的斜率.显然在A(1,2)处取得最大值2.在x轴上的线段BC上时取得最小值0，∴选C.

点评：深刻地理解目标函数的含义，正确地将其转化为直线的斜率是解决本题的关键。

2.平面内两点间的距离型（或距离的平方型）

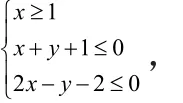
[解析]：目标函数x2＋y2，其含义是点(0,0)与可行域内的点的距离的平方。画出可行域如下图所示，

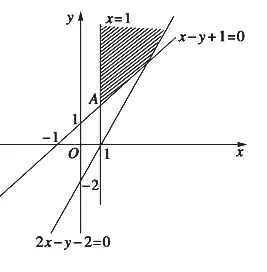
可见可行域中的点A(1,2)到原点距离最小为d＝5，∴x2＋y2≥5.即x2＋y2的最小值为

3.点到直线的距离型

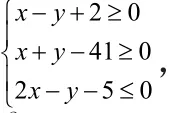
z＝x2＋y2－10y＋25的最小值.

[解析]作出可行域如图所示，并求出顶点的坐标A(1,3)、B(3,1)、C(7,9).

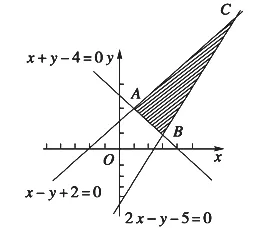
易知可行域内各点均在直线x＋2y－4＝0的上方，

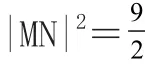
规律方法

解决这类问题的关键是利用图形的直观性，这就需要：第一，要准确作出可行域；第二，要抓住目标函数Z=f(x,y)中z的几何意义。

二、线性规划中的含参类型

1.约束条件中含有参数问题

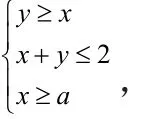
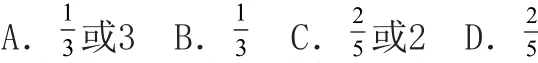
解析：求解有关线性规划的最大值和最小值问题，准确画图找到可行域是关键.

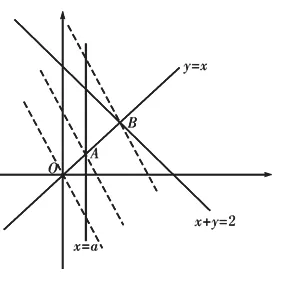
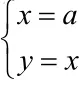
∴Zmax=3,Zmin=3a.

由题意得a-故答案B。

规律方法：

要使目标函数在含参的可行域中取得最值,可以利用函数的数形结合思想,比较约束条件中的直线斜率大小,找到最优解,然后再代入目标函数求出参数的值

2.线性目标函数中含参数类型

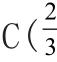
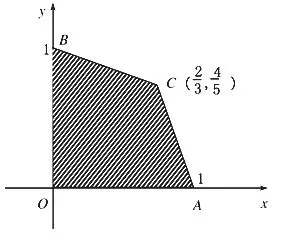
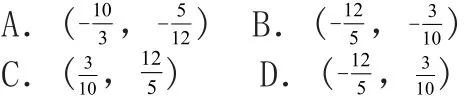
[答案] B

[解析] y＝ax－z.在C点取最优解，则一定是z的最小值点，.结合选项可知选B.

规律方法：

1.准确画出可行域是解答此类问题的前提条件。

2.把目标函数值与过可行域内点的一组平行直线建立对应关系。

3.理解好目标函数的几何意义是关键。

准确定位好之后把目标函数中直线的斜率约束条件中的直线斜率比较大小从而求出参数的范围。