一道课本习题的改编与赏析

广东省惠州市惠阳区华南师范大学附属惠阳学校 林永珍

下面，我就新人教版就年级上册第十三章旋转复习巩固习题76页第5题进行改编赏析。

原题：如题如图（1），△ABC和△ECD都是等边三角形，△ECB可以看做是△DAC经过平移、轴对称或旋转得到．说明得到△EBC的过程；

解：（1）∵△ECD是等边三角形，

∴CD=CE，∠DCE=60°，

同理CA=CB，∠ACB=60°

∴以点C为旋转中心将△DAC逆时针旋转60°就得到△EBC；

本题以等边三角形为载体，对于旋转问题，首先应明确旋转的性质，哪个是旋转中心，哪些线段是相等的，哪些角是相等的，要用旋转的眼光去观察和研究图形，把握图形旋转的性质。

改编一：如图（2），连接P、Q，求证：△PCQ为等边三角形．

证明∵△BCE≌△ACD，

∴∠CAD=∠CBE，

∵∠BCA=∠DCE=60°，

在△A Q C和△B P C中，∠CAQ=∠CBP，∠ACQ=∠BCP ，AC=BC

∴△ACQ≌△BCP（AAS），

∴CP=CQ，

∴△CPQ是等边三角形．

改编二：△ABC和△ECD都是等边三角形

（1）如图1，若B、C、D三点在一条直线上，求证：BE=AD；

（2）保持△ABC不动，将△ECD绕点C顺时针旋转，使∠ACE=90°（如图2），BC与DE有怎样的位置关系？说明理由．

题目分析：（1）利用等边三角形的性质和已知条件证明△ACD≌△BCE即可；（2）BC垂直平分DE，延长BC交DE于M，证明∠ECM=∠DCM，利用三线合一证明即可．

证明：∵△ABC和△ECD都是等边三角形，∴AC=BC，EC=DC，∠ACB=∠ECD=60°.

∴∠ACB+∠ACE=∠ECD+∠ACE，即∠ACD=∠BCE.

∴△ACD≌△BCE.∴AD=BE.

（2）BC垂直平分DE，理由如下：

如图，延长BC交DE于M，

∵∠ACB=60°，∠ACE=90°，∴∠ECM=180°-∠ACB-∠ACE=30°.

∵∠DCM=∠ECD-∠ECM=30°，∴∠ECM=∠DCM.

∵△ECD是等边三角形，∴CM垂直平分DE，即BC垂直平分DE．

试题赏析：本题以三角形为背景，以线段和角的关系为目标，整合三角形的性质，全等的判断等知识，充分体现了中考数学考试说明中的以问题为载体，以知识为基础，以思维为主线，以能力为目标，全面考查学生的学习潜能，力求体现出重视基础，关注思想，加强应用，发展能力的试题特征，与学业考试的目标指向：有利于减负，有利于教育均衡相一致，的指导思想，教与学立足于基础，注重创新思维的训练，注重学生解决问题能力的培养，力争做到发挥好一个问题背景的作用。

改编三：如图，已知△B A D和△B C E均为等腰直角三角形，∠BAD=∠BCE=90°，点M为DE的中点，过点E与AD平行的直线交射线AM于点N．

（1）当A，B，C三点在同一直线上时（如图1），求证：M为AN的中点；

（2）将图1中的△BCE绕点B旋转，当A，B，E三点在同一直线上时（如图2），求证：△ACN为等腰直角三角形；

（3）将图1中△BCE绕点B旋转到图3位置时，（2）中的结论是否仍成立？若成立，试证明之，若不成立，请说明理由．

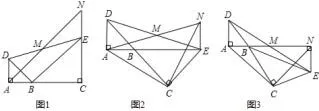
证明：如图1∵EN∥AD，

∴∠MAD=∠MNE，∠ADM=∠NEM．

∵点M为DE的中点，

∴DM=EM．

∴在△ADM和△NEM中，

∴△ADM≌△NEM∴AM=MN∴M为AN的中点

（2）证明：如图2，∵△BAD和△BCE均为等腰直角三角形，

∴A B=A D，C B=C E，∠CBE=∠CEB=45°

∵AD∥NE，

∴∠DAE+∠NEA=180°．

∵∠DAE=90°，

∴∠NEA=90°．

∴∠NEC=135°．

∵A，B，E三点在同一直线上，

∴∠ABC=180°-∠CBE=135°．

∴∠ABC=∠NEC．

∵△ADM≌△NEM（已证），

∴AD=NE．

∵AD=AB，

∴AB=NE．

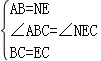
在△ABC和△NEC中，

∴△ABC≌△NEC．

∴AC=NC，∠ACB=∠NCE．

∴∠ACN=∠BCE=90°．

∴△ACN为等腰直角三角形．

（3）△ACN仍为等腰直角三角形．

证明：如图3，此时A、B、N三点在同一条直线上．

∵AD∥EN，∠DAB=90°，

∴∠ENA=∠DAN=90°．

∵∠BCE=90°，

∴∠CBN+∠CEN=360°-90°-90°=180°．

∵A、B、N三点在同一条直线上，

∴∠ABC+∠CBN=180°．

∴∠ABC=∠NEC．

∵△ADM≌△NEM（已证），

∴AD=NE．

∵AD=AB，

∴AB=NE．

在△ABC和△NEC中，

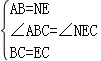
∴△ABC≌△NEC．

∴AC=NC，∠ACB=∠NCE．

∴∠ACN=∠BCE=90°．

∴△ACN为等腰直角三角形

试题赏析：本题考查了全等三角形的判定与性质、平行线的性质、等腰直角三角形的判定与性质、多边形的内角与外角等知识，渗透了变中有不变的辩证思想，是一道好题．将课本原题中的等边三角形改为了等腰直角三角形，通过类比联想引申拓展，可以达到解一题会一类的目的。

通过教材例习题的开发与利用使学生的思维能力、应用意识、分析问题和解决问题的能力在原有基础上锝到一次升华。对于教材二次开发，能满足不同学生的需求，培养学生的学习兴趣，让学生真正理解教学内容，活学活用，提高教学的效率，习题的“改编”能促使学生的学习方式由“重结论轻过程”向“过程与结果”并重的方向发展，使学生挖掘隐含问题的本质属性，从而达到“做一题，通一类，会一片”的解题境界．正如数学教育家波利亚指出的：“一个有责任性的教师穷于应付繁琐的数学内容和过量的题目，还不如适当选择某些有意义但有不太复杂的题目去帮助学生发掘题目的各个方面，在指导学生的解题过程中，提高他们的才智和解题能力．”为此，我们应该关注并参阅对例题、习题处理的相关知识“借题发挥”，结合案例分析，紧紧围绕新课程标准标的要求进行探究，以期促进学生学会从多层次、广视角，全方位的认识、研究问题，从而提高课堂教学的有效性和专业化发展和专业水平。