基于深度学习的配对交易策略

叶映彤+蔡熙腾+李雅妮+蔡向高

摘 要：随着我国金融创新的推进，量化交易逐渐在我国证券市场中发芽成长。量化交易领域中传统的配对交易策略，都假设股价之间满足某种特定的关系，因而存在着局限性。运用深度学习技术，可以避免在配对交易中引入前提额外假设，而是将挖掘规律的任务交给计算机来完成。使用栈式自动编码器代替传统方法，挖掘股票价格相关性中蕴含的套利机会，能形成一套新的、有着独立逻辑的交易策略。实验表明，该策略在我国A股市场表现出稳定的盈利能力，在根据近两年A股市场数据的模拟测试中，日胜率为62.9%，信息比率为0.378。

关键词：量化交易 配对交易 深度学习 栈式自动编码器 A股市场

中图分类号：TP39 文献标识码：A 文章编号：1674-098X（2017）02（c）-0247-06

Abstract：Quantitative trading strategy has emerged in recent years as quantitative trading gains more and more attention in China. Traditional trading strategies such as Pairs Trading Strategy always simplify the relation among assets price due to the difficulties inmodeling non-linear properties. This paper aims to seek an artificial intelligence approach based on Deep Learning technique for designing trading strategies. The widely used Auto-Encoder is a Multi-layer Neural Network which has shown its capability in modeling non-linear properties of complex data. In this paper， we propose an Auto-Encoder based approach for Pairs Trading Strategy. Experiment results demonstrate that the proposed strategy shows excellent performance in Chinese A-share stock market with Win-Rate which is 62.9% and Information Ratio which is 0.378.

Key Words：Quantitative Trading；Pairs Trading；Deep Learning；AutoEncoder；A-share Market

配對交易策略就是一种经典的量化交易策略，其基本思想来源于20世纪20年代华尔街传奇交易员Jesse Livermore的姐妹股票对（Sister stocks）交易策略。其关键点在于找到高度相关的股票对以及股票对的股价之间存在着的数量关系[1]，这也是配对交易的难点所在。目前该领域主要有四种传统方法，包括相关系数法、Vidyamurthy在2004年提出的协整法[2]、Elliott等在2005年提出的随机价差法[3]、以及Gatev等在2006年提出的最小距离法[4]。但是这些方法都有一个共同的局限性，它们都寄希望于所有股票对的价差都满足假定的模式。而事实上股票对之间的价格关系可能千变万化，不能一概而论。这些方法寻找到的股票对很可能只是其中一个很小的子集。而且传统方法常常只能用于寻找两只股票之间的线性关系，对于多只股票之间的非线性关系往往无能为力。

深度学习是一类新兴的多层神经网络学习算法，因其缓解了传统训练算法的局部最小性，引起机器学习领域的广泛关注[5]。深度学习通过组合低层特征形成更加抽象的高层表示（属性、类别或特征），以发现数据的分布式特征表示，实现对复杂的高维非线性函数的逼近。用深度学习技术替换配对交易策略中的传统方法，来寻找高度相关的股票对，以及股票对的股价之间存在着的数量关系，有利于挖掘更多复杂的、更隐蔽的非线性盈利机会，也可以很容易地扩展到在大量的证券中寻找套利机会。

该文拟用深度学习中的栈式自动编码器作为基本模型，参考配对交易策略中的基本思想，设计一种能够自动从股票相关性中挖掘套利机会，并通过买入或卖的基本思想，设计一种能够自动从股票相关性中挖掘套利机会，并通过买入或卖出股票实现盈利的量化交易策略。此外，该文还使用了基于历史数据的测试来验证这种策略在实战中的价值。

1 基于深度学习的配对交易策略

1.1 基本思想

不同股票的价格直接具有很高的相关性，常常表现为同涨同跌。一般来说，可以将股票价格的变动分为两大部分，包括大盘趋势带来的变动和个股自身的变动。配对交易策略就是关注两种相关性极高的股票，猜测两只股票价格存在一定的数量关系，在两只股票价格偏离该数量关系的时候，预期价格会恢复正常，所以选择买入价格偏低的股票，卖出价格偏高的股票；如果之后两只股票的价格确实恢复了原来的数量关系，那么就能实现盈利。

基于深度学习的配对交易策略具体是指，选择一只目标股票，假设其股价序列为Y，而除了目标股票以外的股票的股价序列为（X1，X2…Xn），如果找到一个函数h使得h（X1，X2…Xn）≈Y，那么可以将h（X1，X2…Xn）视作一只与目标股票相关性极高（接近于1）的虚拟股票，或者说找到了一个虚拟股票与目标股票组成一个股票对，他们之间存在h（X1，X2…Xn）≈Y的数量关系。套用配对交易策略就可以利用该股票对进行套利。在这里，将通过深度学习用来学习合适的函数h，从而实现（X1，X2…Xn）与Y之后的映射关系。

1.2 数据处理

该文选取了在2004年11月1日前在中国大陆主板市场上市，并截至到2016年2月5日尚未退市的1 356只股票作为股票池，整理得到这些股票自2004年11月1日—2016年2月5日每个交易日的收盘价。其中2004年11月1日—2014年4月13日的数据作为训练数据，2014年4月14日—2016年2月5日的数据作为测试数据。

该文将每100个交易日的数据作为一批，对每批数据进行标准化，使得在同一批数据中，每只股票的价格均值为0，方差为1，并在模型的输出端需要做一个反向处理。最后，从处理好的数据中抽出属于目标股票的数据，作为Y，其余数据作为（X1，X2…Xn）。其中（X1，X2…Xn）是模型的输入（Input），而Y是模型训练的目标（Target）。

1.3 模型建立与训练

该文使用深度学习中的栈式自动编码器作为基本模型，使用了四层自动编码器进行特征提取，然后用单层的神经网络作为最顶层的输出端。

对于第一层自动编码器，输入为数据处理阶段中代表（X1，X2…Xn）的数据，通过向上的权重得到特征，通过向下的权重重新生成数据。其中输入的节点数为1 355，对应除目标股票之外的1 355只股票；隐藏层的节点数为400，对应特征的维度。

对于第二到第四层的自动编码器，输入为上一层编码器学习到特征，并通过向上的权重得到更高层的特征，作为下一层编码器的输入。每一层输入的节点数分别为400、120、35，而对应的隐藏层节点数分别为120、35、10。

对于每一层的编码器，使用的激活函数都是tan?函数。如果向上的权重分别用W（1）、b（1）表示，向下的权重分别用W（2）、b（2）表示，原数据用X表示，新数据用X′表示，隐藏层用a表示，编码的过程可以表示为：

解码过程可以表示为：

整个自动编码器的训练目标就是让新数据与原数据差异尽可能小，使用的代价函数为：

对于最顶层的单层神经网络，输入为第四编码器学习到的特征，输入节点数为10，输出为Y′，即对于目标股票价格Y的预测，使用的激活函数依然是tan?函数。如果该层的权重分别用W、b表示，输入用X表示，目标股票的价格用Y表示，那么该层的输入可以表示为：

类似的，该层的代价函数为

模型建立后需要進行以下训练：使用梯度下降法自下而上逐层训练自动编码器；然后对整个网络进行微调（Fine-tuning），即将第一步得到的权重作为整个网络的初始化权重，然后用反向传播算法训练整个网络。

1.4 交易策略

通过上文模型的建立和训练，我们得到了一个关于目标股票Y的预测Y′。

从传统的配对交易中，一般会选择卖出股票对中估值相对较高的，买入估值相对较低的，从而相对价值回归均值的时候实现盈利。但是该文的策略中存在一个问题，由于自动编码器是非线性的，所以不存在一种方法可以从已有的其他股票中构建出Y′，更无法买入或卖出Y′。因此这里需要采取折中的方法进行交易。方法有很多，以下列举其中三种。

（1）当Y与Y′的价格出现偏差的时候，若Y>Y′，则卖出目标股票；反之则买入目标股票。如果未来Y变动直至Y=Y′，那么将会盈利，但如果Y′变动更大，那么可能不能盈利，甚至亏损。由于不能卖出Y′从而锁定利润，事实上这种方法存在不小的风险。

（2）当Y′价格上涨的时候买入目标股票，反之则卖出目标股票。如果Y与Y′呈同方向的变动，未来可能就能获得利润。

（3）比较Y与Y′的涨幅变化，如果Y′的涨幅大于Y的涨幅，那么买入目标股票；否则卖出目标股票。由于每次只考虑涨幅的变化，如果模型存在累计的误差，那么该方法可以避免之前累计的误差会持续影响之后的交易。

此外，前文提到的都是针对一只目标股票的策略。执行针对一只股票的交易策略时，在买入之后需要等待股票价格恢复到原来的关系。在等待的过程中可能会有暂时性的亏损。在实际操作中，需要针对每一只股票构建栈式自动编码器，并独立地执行交易策略。由于不同股票价格恢复的周期不一致，可能部分股票处于盈利状态，少量股票处于亏损状态，互相抵消之后，能使得加总的收益更加稳定。

2 实证研究

在该文的测试过程中，所有测试都是针对前文数据处理后的测试数据，并使用日胜率（Win-Rate）、信息比率（Information Ratio）等指标来评价策略的表现。

2.1 预测能力

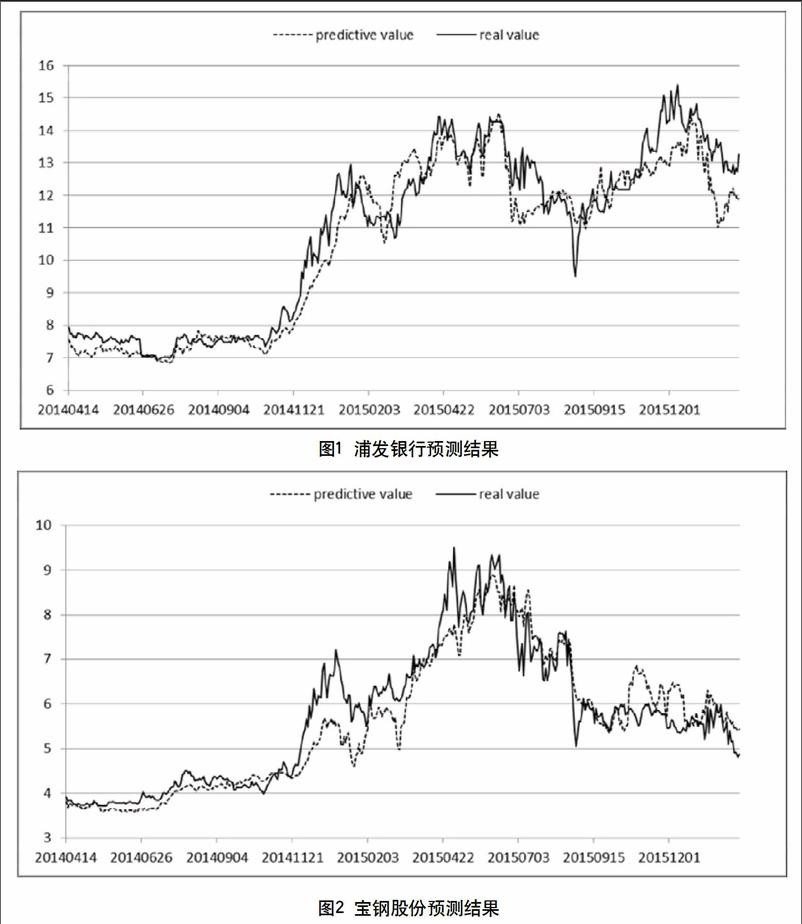
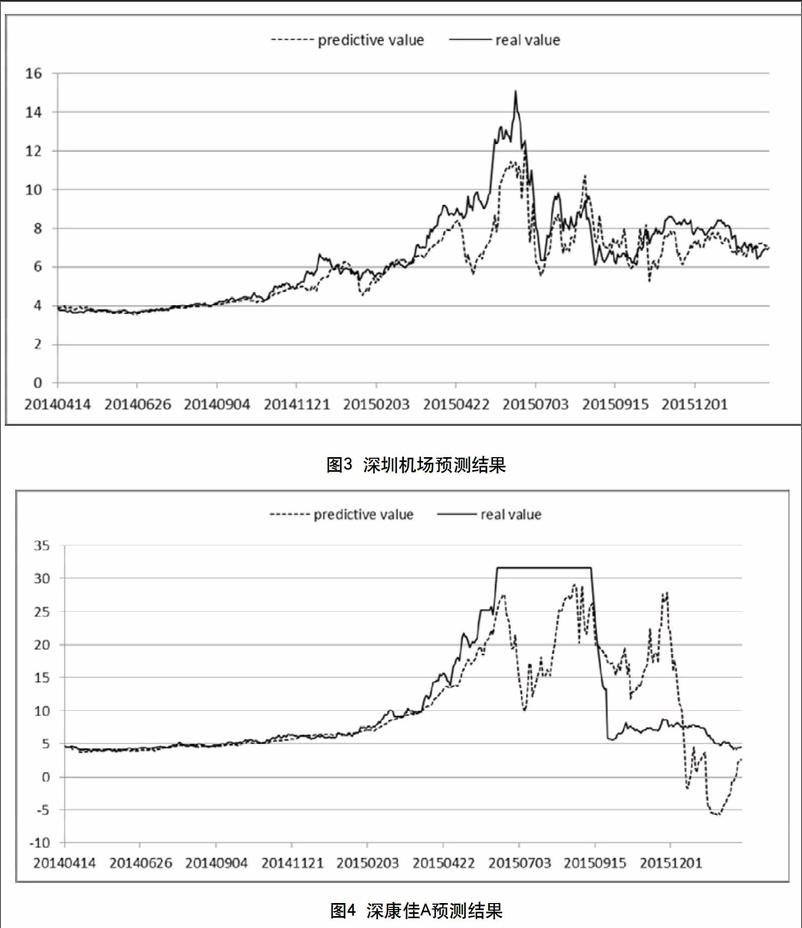
策略有效的第一个关键点在于Y与预测得到的Y′是否呈现类似的变动趋势，是否存在比较稳定的数量关系。这里抽取了浦发银行（600000）、宝钢股份（600019）、深康佳A（000016）、深圳机场（000089）四只股票的预测结果，绘制成图像（见图1～图4）。其中虚线均代表预测得到的Y′，而实线均代表原始的Y。

可以看出，浦发银行、宝钢股份预测的结果是非常好的。深圳机场的预测结果虽然中间一段时间出现比较大的偏离，但最终还是恢复一致了。但深康佳A的预测结果在后半段两条曲线的偏离非常大，这一定程度是由于深康佳A在中间一段出现了停牌，而停牌过后又遭受极端的下跌，在这种情况下应该谨慎使用该模型。

总体而言，模型在绝大部分的情况下表现出了很高的预测能力，预测得到的Y′和原始的Y有着很高的相关性。表1是前面提及的四只股票Pearson相关性检验的结果。虽然深康佳A相对而言相关系数明显要低一些，不过所有股票的检验都通过了相关性检验，而且相关系数都比较接近于1，符合策略的要求。

2.2 单个策略收益

前文提到有3种可以考虑的交易策略，下面逐一用其对浦发银行、宝钢股份深康佳行、宝钢股份深康佳行、宝钢股份深康佳A、深圳机场四只股票进行测试，并计算它们各自的信息比率。见表2。

显然，对于这4种股票，方法2是最优的。事实上，从对大部分股票的效果来看，方法2依然是最优的，而且比其他两个方法的表现好很多。

为了直观地了解策略收益的情况，下面分别绘制了这四只股票使用策略2进行交易的累计超额收益。（如不作特别说明，下文提及的收益均指累计超额收益。）

从图5～图8四个图可以看出，该策略对于不同的股票进行交易都能够获得显著的收益，这说明了策略的盈利能力和适应能力。但是策略对于不同股票的表现并不一致，比如对深康佳A和深圳机场的策略收益明显会更高。另外，对于不同股票，收益的波动性也有所不同。正如之前的假设，少量股票可以在某段时间走势异于大盘，但是大部分股票的走势都是跟随大盘的，少量股票特殊阶段的亏损，可以被其他股票的盈利所抵消。

2.3 组合策略收益

前文提到，对单个股票進行交易的时候，在某个阶段可能出现一定回撤。这是部分股票在特殊时期的异常所导致的。根据现代资产组合理论，将收益相关性低的资产进行组合，实现分散个别风险，提高资产组合收益风险比，这是通过策略的组合实现更高的信息比率的基础。

由于计算量巨大，该文只选择了包括上文所提及四只股票在内的200只股票进行测试，并为它们设置相同的资金权重，依照类似于上文的方法进行测试，得到了高达0.378的信息比率，远高于前文的任何一个结果，策略的收益曲线见图9。

组合策略的收益比单个策略有了不小地提高，在2014年4月14日—2016年2月5日这接近2年的时间内，策略收益超过400%，平均到每日的收益为0.823%（未扣除交易成本）。更重要的是，相对于单个策略，组合策略收益的波动性极大的降低了，出现亏损的几率很低，策略的单日胜率（即跑赢大盘的概率）高达62.9%，回撤的幅度也很小，这代表着这种组合策略有着极稳定的盈利能力，具有投入实战价值。

3 结语

该文从量化交易领域中传统的配对交易策略入手，结合前沿的深度学习技术，运用栈式自动编码器构建一个能够根据股票价格相关性预测股票价格的模型，并生成一个完整的量化交易策略。这种策略无需预先假设股票价格之间关系的形式，而是使用深度神经网络自动地学习这种相关性的特征，从而克服了传统方法的局限性。该文又提出在这种方法的基础上，通过同时对大量的股票独立地执行该策略，构成一个组合策略，从而实现策略收益和稳定性的提高。实验证明，最终的组合策略在我国A股市场中有持续稳定盈利的能力，在根据近两年A股市场数据的模拟测试中，日胜率为62.9%，信息比率为0.378，具备投入实战的价值。

参考文献

[1] 陈豪.配对交易的改进设计[D].广州：华南理工大学，2014：1-21.

[2] Vidyamurthy， G. Pairs Trading： Quantitative Methods and Analysis[M].Chichester：John Wiley&Sons，2004.

[3] Elliott Robert J.Pairs trading[J].Quantitative Finance，2005，5（3）：138-139.

[4] Gatev E.Pairs Trading：Performance of a Relative-Value Arbitrage Rule[J].Review of Financial Studies，2006，19（3）：156-159.

[5] 孙志军.深度学习研究综述[J].计算机应用研究，2012（8）：2806-2810.