一种基于连续区间直觉模糊Theil测度的多属性群决策方法*

罗 敏, 张 志, 周 晗, 吴 群, 陶志富

(1.安徽大学 经济学院，合肥，230601；2.安徽大学 数学科学学院，合肥 230601)

一种基于连续区间直觉模糊Theil测度的多属性群决策方法*

罗 敏1, 张 志1, 周 晗2, 吴 群2, 陶志富1

(1.安徽大学 经济学院，合肥，230601；2.安徽大学 数学科学学院，合肥 230601)

针对区间直觉模糊信息的不确定性，提出了一种基于连续区间直觉模糊Theil(C-IVIFT)测度的多属性群决策方法。首先基于连续区间直觉模糊有序加权平均(C-IVIFOWA)算子定义了连续区间直觉模糊Theil测度，并研究该测度的一些性质；其次，构建以C-IVIFT测度偏差最小化为目标的最优化模型用以确定专家权重和属性权重，进而得到不同方案的综合属性值，并利用相似性函数和精确函数对方案进行排序；最后，通过ERP软件择优实例说明提出的决策方法的合理性和有效性。

多属性群决策；C-IVIFT测度；专家权重；属性权重；区间直觉模糊集

多属性群决策[1-4]是指多个专家针对具有多个属性的有限方案进行排序和选择的一类决策问题。当属性值与属性权重都是确定的实数或语言评价信息时，已有很多成熟的解决方法。考虑现实世界的复杂性和决策信息的模糊性，决策者的属性评价值往往不是确定的实数。Atanassov[5-6]于1986年首次提出直觉模糊集，并于1989年将其拓展至区间环境中，提出了区间直觉模糊集概念，截至目前，基于区间直觉模糊集的相关研究取得了丰富的成果。针对区间直觉模糊多属性决策方法，主要研究集中在：区间直觉模糊数的信息集成算子[7-8]；构建区间直觉模糊信息的一些测度，并将其应用到多属性群决策中，例如相似性测度[9]、灰色关联度[10]和距离测度[11]等；将一些经典的决策方法应用到区间直觉模糊多属性决策中，例如谭春桥[12]基于TOPSIS方法，定义了区间直觉模糊集的接近系数和距离，运用备选方案到正负理想解的距离确定接近系数，并对方案进行排序。高建伟[13]针对准则值为区间直觉模糊数，准则权重分别为完全未知和部分已知的多准则决策问题，提出一种基于前景理论的决策分析方法等。

针对区间直觉模糊多属性群决策问题，考虑到决策者的偏好、知识结构等方面存在差异，决策结果可能不同，因此有必要综合各决策者的属性评价信息。此时，如何确定决策者权重尤为关键。文献[14]针对属性权重完全未知的决策问题, 首先定义了区间直觉模糊熵, 其次通过熵衡量每一属性所含的信息量来求解属性权重。在区间直觉模糊框架中引入交叉熵，以此确定决策者权重。Yue[15]利用相似测度的方法度量个体与专家群体决策的差异，进而确定最优的专家权重。

Theil不等系数是用来衡量两组数据偏差程度的一种度量方式，文献[16-17]将其应用于组合预测模型中。本文在现有研究的基础上，将Theil不等系数拓展至区间直觉模糊环境中，考虑决策者的乐观系数，提出了一种基于连续区间直觉模糊Theil(C-IVIFT)测度，并将其应用到多属性群决策问题中。首先基于连续区间直觉模糊有序加权平均(C-IVIFOWA)算子提出了Theil不等系数测度公式，然后构建多目标规划模型确定信息完全未知的属性权重和专家权重，进一步建立一种新的区间直觉模糊多属性群决策方法，并将其应用于ERP软件的选择过程中。

1 基本知识

定义1[5]设Y为给定论域，定义在Y上的直觉模糊集E表示为

(1)

其中，μE(y)和νE(y)分别表示y∈Y属于E的隶属度和非隶属度，即μE:Y→[0,1],y∈Y→μE(y)∈[0,1],νE:Y→[0,1],y∈Y→νE(y)∈[0,1]，且∀y∈Y，满足μE(y)+νE(y)∈[0,1]。

此外，论域Y中元素y属于E的犹豫度可表示为πE(y)=1-μE(y)-νE(y)。为简化表示，记β=(μβ,νβ)为直觉模糊数。

设β=(a,b)，β1=(a1,b1)，β2=(a2,b2)为直觉模糊数，其运算遵循下列规则[4]：

(2)

(3)

(4)

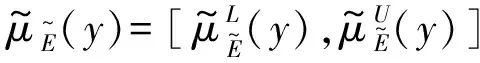
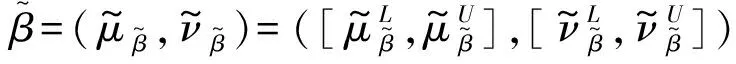
(5)

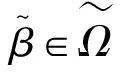
(6)

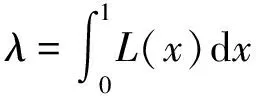
(7)

(8)

(9)

其中，πλ根据式(2)计算可得。

定义5 设βλ,1=(aλ,1,bλ,1)和βλ,2=(aλ,2,bλ,2)为任意两个含参数λ的直觉模糊数，则它们的大小比较方法定义如下：

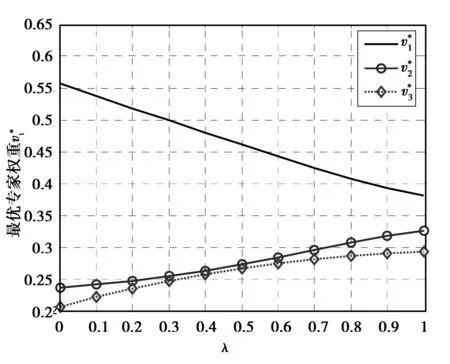
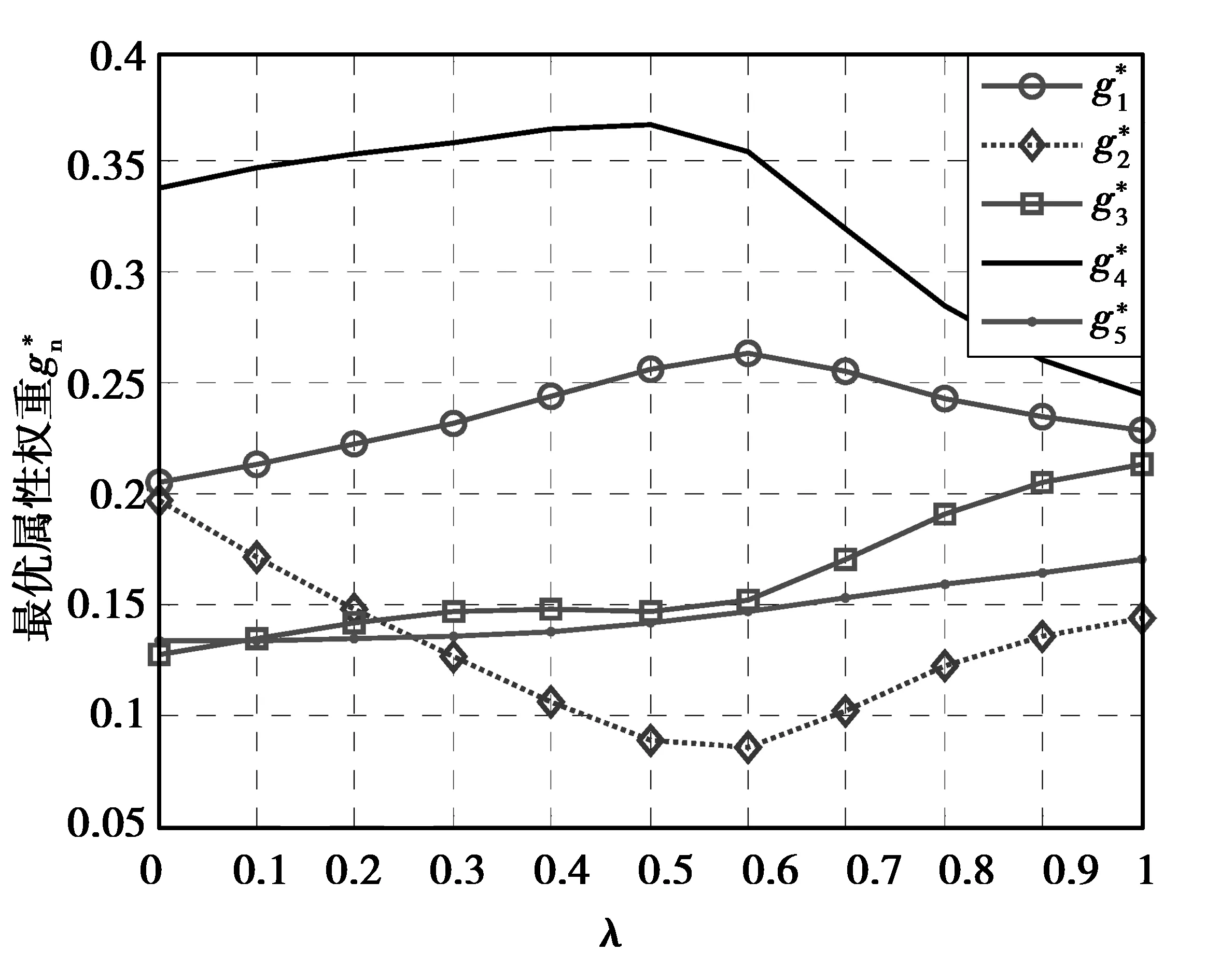
(1) 若pλ(βλ,1)

(2) 若pλ(βλ,1)=pλ(βλ,2)，

a) 当qλ(βλ,1)=qλ(βλ,2)，则βλ,1=βλ,2；

b) 当qλ(βλ,1)

c) 当qλ(βλ,1)>qλ(βλ,2)，则βλ,1>βλ,2。

2 连续区间直觉模糊Theil测度

定义6 设ηλ=(αλ,1,αλ,2,…,αλ,n)和γλ=(βλ,1,βλ,2,…,βλ,n)为论域Y上含参数λ的直觉模糊向量，若函数f:Ω×Ω→R满足:

(10)

容易证明，直觉模糊向量ηλ和γλ间的C-IVIFT测度满足下列性质：

(1)fλ(ηλ,γλ)≥0；

(2) 当ηλ=γλ时，fλ(ηλ,γλ)=0；

(3)fλ(ηλ,γλ)=fλ(γλ,ηλ)。

3 基于C-IVIFT测度的区间直觉模糊多属性群决策方法

3.1 区间直觉模糊多属性群决策问题的基本描述

若un为成本型，令

(11)

若un为效益型，令

(12)

3.2 基于C-IVIFT测度的专家权重确定模型

合理的专家权重下，各专家的决策矩阵应与集成后的专家综合矩阵保持较小的偏差，C-IVIFT测度可用来度量此种偏差。

(13)

3.3 基于C-IVIFT测度的属性权重确定模型

假设属性权重为G=(g1,g2,…,gN)T，本小节主要研究运用C-IVIFT测度确定属性权重的方法。

为求解最优的属性权重，不同属性列lλ,n与综合属性列Wλ的C-IVIFT测度总是越小越好，且lλ,n与Wλ比较的概率是均等的，由此建立下述最优化模型：

(14)

3.4 新的区间直觉模糊多属性群决策方法具体步骤

综上所述，在专家权重和属性权重完全未知情况下，给出一种基于C-IVIFT测度的区间直觉模糊多属性群决策方法：

Step 5：根据公式(8)计算不同综合属性值wλ,m(m=1,2,…,M)的相似性函数rλ,m=pλ(wλ,m)。

Step 6：根据不同方案对应的相似性函数值rλ,m的大小对方案进行排序。

Step 7：结束。

4 案例分析

Step 4：求解模型式(14)，得最优属性权重G*=(0.256 4,0.088 3,0.146 9,0.367 2,0.141 2)T和最优综合属性列：

Step 5：计算不同ERP软件的相似性函数值rλ,m，得到：

rλ,1=0.296 6，rλ,2=0.266 4

rλ,3=0.270 7，rλ,4=0.276 9

rλ,5=0.2648

Step 6：将rλ,m进行升序排列：rλ,5

x1>x4>x3>x2>x5

可以看出，最优方案为x1，即综合考虑3位决策者的评价，ERP软件x1为最优选择。

为了考虑不同态度参数对最优专家权重和属性权重的影响，取λ=[0,1]，得最优专家权重和属性权重的变化图：

图1 参数λ对最优专家权重的影响Fig.1 Influence of parameter λ on optimal expert weights

图2 参数λ对最优属性权重的影响Fig.2 Influence of parameter λ on optimal expert weights

根据图1，专家2和3的权重均在0.38以下，并随态度参数λ的增加单调递增，在决策中的重要性程度逐渐增加。与之相反，专家1的权重随态度参数λ的增加单调递减，且由λ=0时的0.557 5到λ=1时的0.206 2，下降幅度达0.351 3。根据图2可以看出，专家进行评价时，软件的销量始终是最重要的属性，维护成本次之。功能的完善性随参数λ的增加先下降后上升，系统抗风险能力和系统风险单调递增，当λ∈[0,0.2]时，功能完备性较系统抗风险能力和系统风险较为重要。 当λ∈(0.2,1]时，恰好相反。

同时，态度参数的变化对综合属性的相似性函数值产生影响，如图3所示：

图3 参数λ对相似性的影响Fig.3 Influence of parameter λ on similarity

可以看出，不同方案的相似性函数值均在一定范围内波动，且单调递减，这反映了态度参数对决策结果的影响。由图3可知，ERP软件1始终是最优方案，当λ∈[0,0.8]时，不同软件的排序为x1>x4>x3>x2>x5；当λ∈(0.8,1]时，决策者的态度较为乐观，此时ERP软件的排序结果发生改变，表示为x1>x4>x3>x5>x2。

5 结 语

目前，大多数多属性群决策问题研究中常常假定专家权重或属性权重已知，忽略了决策者的风险规避程度对方案排序的影响。本文基于连续区间直觉模糊有序加权平均(C-IVIFOWA)算子，结合Theil不等系数，提出C-IVIFT测度。通过构建偏差最小的多目标规划模型，确定专家权重和属性权重，并提出一种基于C-IVIFT测度的区间直觉模糊多属性群决策方法。最后运用算例证实了该方法的可行性和有效性。

[1] 廖虎昌.复杂模糊多属性决策理论与方法[M].北京：科学出版社,2016

LIAO H C.Theory and Method for Complicated Fuzzy Multiple Attribute Decision Making[M].Beijing:Science Press,2016

[2] 吴群，吴澎，周礼刚.基于联系数的区间二元语义模糊多属性群决策方法[J].重庆工商大学学报(自然科学版),2016,33(1):1-8

WU Q,WU P,ZHOU L G.Interval 2-tuple Linguistic Fuzzy Multiple Attributes Group Decision-making Based on Connection Variables[J].Journal of Chongqing Technology and Business University (Natural Science Edition),2016,33(1):1-8

[3] ZHOU L,TAO Z,CHEN H,et al.Continuous Interval Valued Intuitionistic Fuzzy Aggregation Operators and Their Applications to Group Decision Making[J].Applied Mathematical Modelling,2014,38(s7-8):2190-2205

[4] 汪新凡.基于联系数纯语言多属性群决策方法[J]．重庆工商大学学报(自然科学版),2006,23(6):580-584

WANG X F.Pure-Linguistic Information Multi-Attribute Group Decision Making Method Based on Connection Number[J]．Journal of Chongqing Technology and Business University ( Natural Science Edition),2006,23(6):580-584

[5] ATANASSOV K.Intuitionistic Fuzzy Sets[J].Fuzzy Sets and Systems,1986,20:87-96

[6] ATANASSOV K,GARGOV G.Interval Valued Intuitionistic Fuzzy Sets[J].Fuzzy Sets and Systems,1989,31(3):343-349

[7] 徐泽水.直觉模糊信息集成理论及应用[M].北京：科学出版社,2008

XU Z S.Intuitionsitic Fuzzy Information Aggregation:Theory and Application[M].Beijing:Science Press,2008

[8] 周晓辉,姚俭,徐磊,等.区间直觉模糊几何Heronian平均算子及其应用[J].系统工程,2016,34(4):140-146

ZHOU X H,YAO J,XU L,et al.Interval Valued Intuitionistic Fuzzy Geometric Heronian Means and Its Application[J].Systems Engineering,2016,34(4):140-146

[9] 徐泽水.区间直觉模糊集相似性测度及其在模式识别中的应用(英文)[J].东南大学学报(英文版),2007,23(1):139-143

XU Z S.On Similarity Measures of Interval Valued Intuitionistic Fuzzy Sets and Their Application to Pattern Recognitions[J].Journal of Southeast University (English Edition),2007,23(1):139-143

[10] 刘勇,Jeffrey Forrest,刘思峰,等.基于区间直觉模糊的动态多属性灰色关联决策方法[J].控制与决策,2013,28(9):1303-1308

LIU Y,FORREST J,LIU S F,et al.Dynamic Multiple Attribute Grey Incidence Decision Making Method Based on Interval Valued Intuitionisitc Fuzzy Number[J].Control and Decision,2013,28(9):1303-1308

[12] 谭春桥.基于区间值直觉模糊集的TOPSIS多属性决策[J].模糊系统与数学,2010,24(1):92-97

TAN C Q.TOPSIS Multiple Attribute Decision Making Based on Interval Valued Intuitionistic Fuzzy Sets[J].Fuzzy Systems and Mathematics,2010,24(1):92-97

[13] 高建伟，刘慧晖，谷云东.基于前景理论的区间直觉模糊多准则决策方法[J].系统工程理论与实践,2014,24(12):3175-3181

GAO J W,LIU H H,GU Y D.Interval Valued Intuitionistic Fuzzy Multi-Criteria Decision Making Method Based on Prospect Theory[J].System Engineering Theory & Practice,2014,24(12):3175-3181

[14] 张英俊,马培军,苏小红,等.属性权重不确定条件下的区间直觉模糊多属性决策[J].自动化学报,2012,38(2):221-228

ZHANG Y J,MA P J,SU X H,et al.Multi-Attribute Decision Making with Uncertain Attribute Weight Inform-ation in the Framework of Interval Valued Intuitionistic Fuzzy Set[J].Acta Automatica Sinica,2012,38(2):221-228

[15] YUE Z.Deriving Decision Maker’s Weights Based on Distance Measure For Interval Valued Intuitionistic Fuzzy Group Decision Making[J].Expert Systems with Applications,2011,38(9):11665-11670

[16] 周礼刚,陈华友,丁子千,等.基于Theil不等系数的IOWGA算子组合预测模型[J].安徽大学学报(自然科学版),2010,34(1):1-6

ZHOU L G,CHEN H Y,DING Z Q,et al.The Combination Forecasting Model Based on the Theil Coefficient and Induced Ordered Weighted Geometric Averaging (IOWGA) Operator[J].Journal of Anhui University (Natural Science Edition),2010,34(1):1-6

[17] 陈华友.基于Theil不等系数的组合预测模型的性质[J].电子科技大学学报,2004,33(1):105-108

CHEN H Y.Properties of Combination Forecasting Models Based on Theil Coefficient[J].Journal of UEST of China,2004,33(1):105-108

[18] 戚筱雯,梁昌勇,张恩桥,等.基于熵最大化的区间直觉模糊多属性群决策方法[J].系统工程理论与实践,2011,31(10):1940-1948

QI X W,LIANG C Y,ZHANG E Q,et al.Approach to Interval Valued Intuitionistic Fuzzy Multiple Attributes Group Decision Making Based on Maximum Entropy[J].Systems Engineering Theory & Practice,2011,31(10):1940-1948

[19] WU Q,WU P,ZHOU Y Y,et al.Some 2-tuple Linguistic Generalized Power Aggregation Operators and Their Applic-ations to Multiple Attribute Group Decision Making[J].Journal of Intelligent and Fuzzy Systems,2015,29(1):423-436

[20] ZHANG X,XU Z.A New Method for Ranking Intuitionistic Fuzzy Values and Its Application in Multi-Attribute Decision Making[J].Fuzzy Optimization and Decision Making,2012,11(2):135-146

责任编辑：李翠薇

An Approach to Multiple Attribute Group Decision Making Based on the Continuous Interval-Valued Intuitionistic Fuzzy Theil Measure

LUO Min1, ZHANG Zhi1, ZHOU Han2, WU Qun2, TAO Zhi-fu1

(1. School of Economics, Anhui University, Anhui Hefei 230601, China; 2. School of Mathematical Sciences, Anhui University, Anhui Hefei, 230601, China)

With respect to the uncertainty of interval-valued intuitionistic fuzzy information, an approach to multiple attribute group decision making on the basis of continuous interval-valued intuitionistic fuzzy Theil (C-IVIFT) measure is investigated. Firstly, a C-IVIFT measure based on the continuous interval-valued intuitionistic fuzzy ordered weighted averaging (C-IVIFOWA) operator is introduced, some desirable properties are discussed as well. Then, two programming models are constructed to derive the optimal weights of experts and attributes with the principle of minimum C-IVIFT measure deviation. Moreover, similarity function and exact function are provided to rank the collective attribute values of alternatives. Finally, an example related to ERP software selection is provided to illustrate the feasibility and effectiveness of the proposed approach.

multiple attribute group decision making; C-IVIFT measure; expert weights; attribute weights; interval-valued intuitionistic fuzzy sets

10.16055/j.issn.1672-058X.2017.0003.011

2016-11-23；

2016-12-30. * 基金项目：国家自然科学基金(71371011,71301001,71501002);安徽省振兴计划优秀青年人才支持项目;安徽大学博士科研启动基金;安徽大学科研训练计划(KYXL2016006);安徽大学创新创业实验项目(201610357473,201610357119,201610357347,201610357348,201610357349,201610357083).

罗敏(1996-)，女，安徽合肥人，从事金融统计研究.

C934

A

1672-058X(2017)03-0056-09