具有唯一平衡点的四维超混沌Lü-like系统的研究*
2017-06-19张艳红杨启贵
张艳红, 杨启贵
(华南理工大学 数学学院,广州 510640)
具有唯一平衡点的四维超混沌Lü-like系统的研究*
张艳红, 杨启贵**
(华南理工大学 数学学院,广州 510640)
基于三维Lü混沌系统,利用反馈控制技术,提出了一个具有5个参数和3个非线性项的新四维自治超混沌系统,并研究该系统的动力学性质;所得新系统具有唯一平衡点,讨论了对应平衡点的稳定性,同时严格证明了Hopf分岔的局部动力学行为;进一步通过分岔图、Lyapunov指数及Poincaré映射等数值分析,验证了系统的超混沌吸引子、混沌吸引子及周期吸引子的存在性。
Lü系统;四维超混沌系统;Lyapunov指数;稳定性;Hopf分岔
自1963年美国科学家Lorenz首次发现第一个混沌吸引子以来,Lorenz系统[1]被认为是第一个把混沌抽象出来的数学模型,它在混沌学的发展中始终占有重要的地位,为现代混沌理论研究奠定了坚实的基础。同时高维非线性系统中通常会产生超混沌现象,此现象是由德国科学家Rössler[2]于1979年发现的,他利用计算机仿真得到了第一个超混沌系统,即Rössler超混沌系统,其系统维数是四维。由于超混沌系统吸引子的轨道在两个或两个以上的方向上扩张,其动力学行为比混沌系统更加复杂,相应的随机性和不可预测性也更强。超混沌在非线性理论及电子技术等领域有着更广泛的应用,其研究方向涉及保密通信、非线性电路和神经网络等,从而超混沌系统的研究具有更广阔的发展前景。迄今对超混沌系统的研究没有一个统一有效的方法,因而讨论超混沌系统是比较困难的,目前一些超混沌系统是在混沌系统基础上通过加上一个线性反馈或其他方法得到的[3-5]。
现今超混沌系统的复杂动力学行为还未能全部被科学家们所掌握,因而超混沌理论仍处于起步的阶段,超混沌系统仍需进一步更深入的研究。由于在连续自治系统中,超混沌系统的研究逐渐引起了数学及相关学科的科学家的广泛关注,人们利用各种方法实现了从混沌到超混沌系统的转化,得到了一系列超混沌系统。由于超混沌产生的最低维数是四维,因此,四维超混沌系统研究具有特殊意义,对于四维超混沌系统的研究,除了Rössler超混沌系统外,1986年,Matsumoto等[6]在研究一个简单的四阶电子电路时发现了超混沌现象,这也是第一次在实际的物理模型中发现的超混沌。后续研究还有Kapitaniak等[7]将两个Chua电路耦合生成超混沌系统;Li等[8]在广义Lorenz型系统的基础上,通过增加反馈控制项得到超混沌系统;利用反馈控制项,Yang等[9-10]研究了Lorenz型超混沌系统。
对于混沌理论,平衡点的个数对理解复杂的动力学行为具有重要的作用。到目前为止,大多数的超混沌系统研究的是有限或可数个孤立平衡点。本文在Lü系统的基础上,通过设计反馈控制器,在其第一个方程上加一个线性反馈,在第二个方程上加上一个正弦扰动项得到一个新的具有唯一平衡点的四维系统,即具有两个正的Lyapunov指数的四维Lü-like超混沌系统。通过对系统的深入分析,研究了复杂的局部动力学行为:平衡点的稳定性及Hopf分岔等.然后讨论了新系统的全局动力学行为,利用分岔图、Lyapunov指数、Poincaré映射等数值验证特有的超混沌动力学性质,当选取适当参数时,超混沌系统可以产生超混沌吸引子、混沌吸引子和周期吸引子等复杂动力学行为。
1 新四维超混沌系统的提出
基于Lü系统[11]:
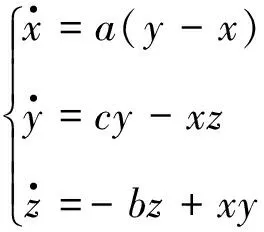
(1)
当参数取a=36,b=3,c=20 时,系统(1)存在混沌吸引子,其相图如图1所示。
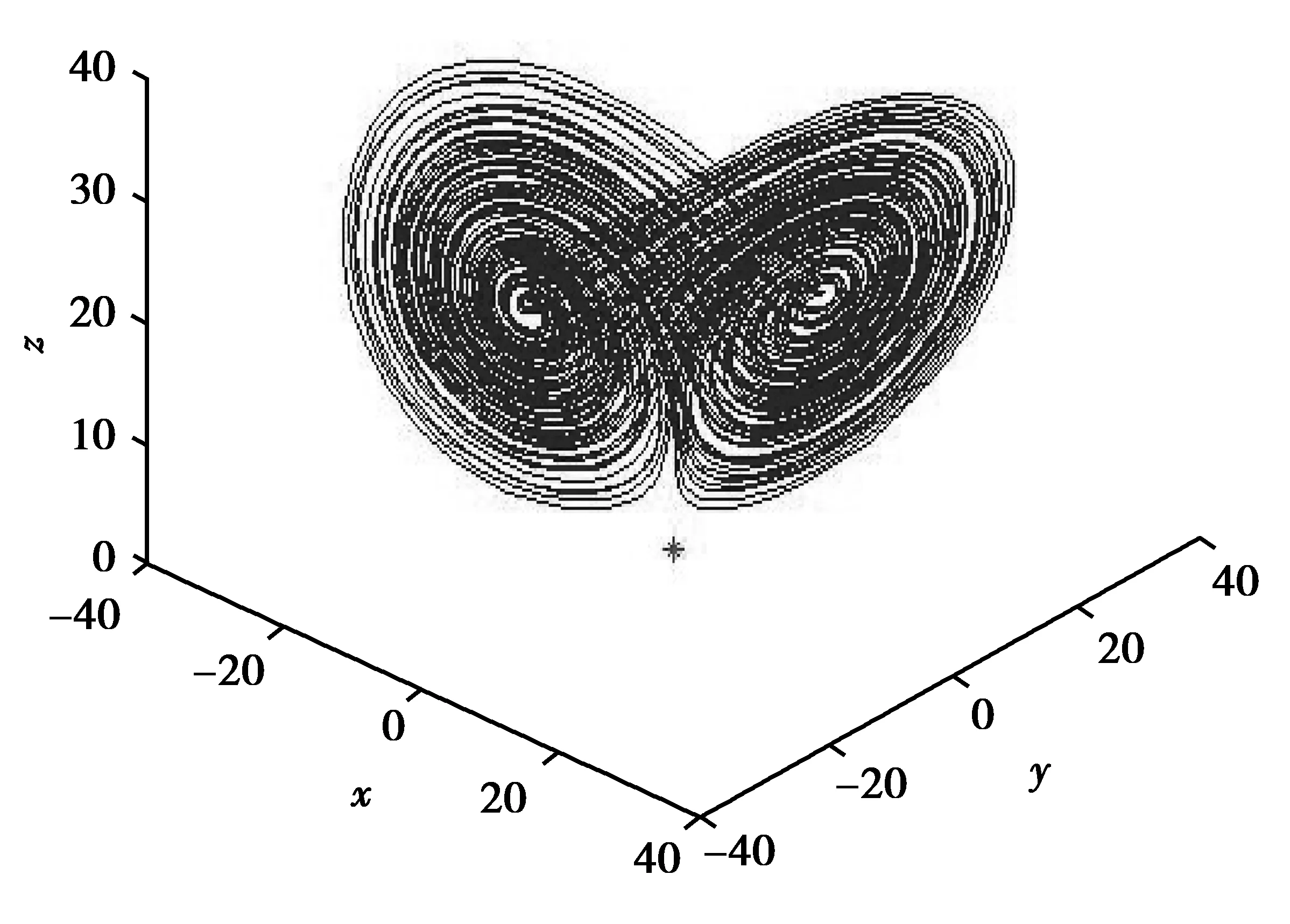
图1 系统(1)的混沌吸引子:(a,b,c)=(36,3,20)Fig.1 Chaotic attractor of system (1): (a,b,c)=(36,3,20)
利用反馈控制技术,在Lü系统(1)的第一个方程加一个线性反馈,在第二个方程加一个正弦扰动项得到一个新的四维系统:

(2)
其中,参数(a,b,c,e,f)∈R5并满足b,c,f≠0。易知系统(2)存在唯一平衡点O(0,0,0,0)。
新四维系统(2)的散度是
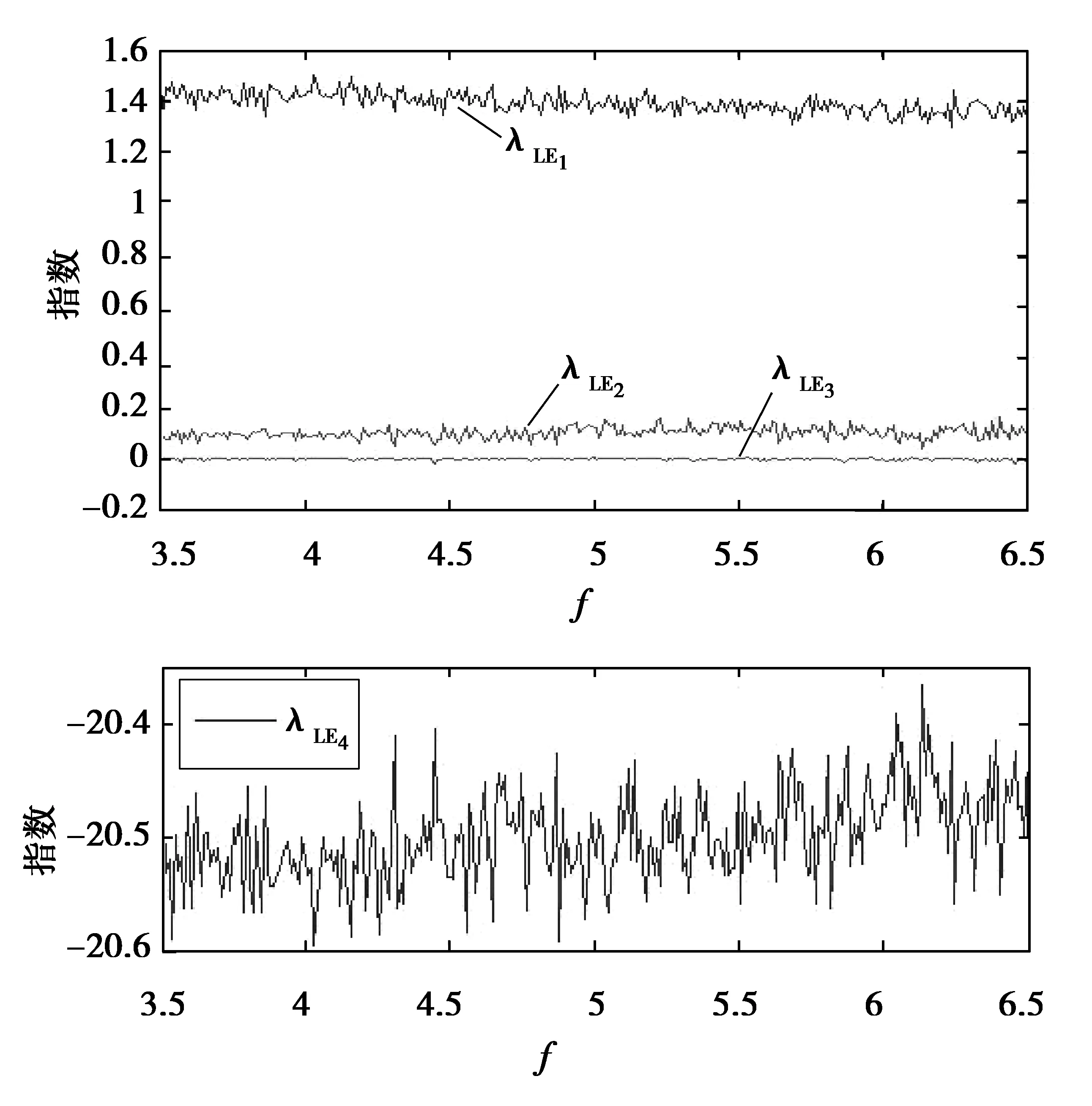
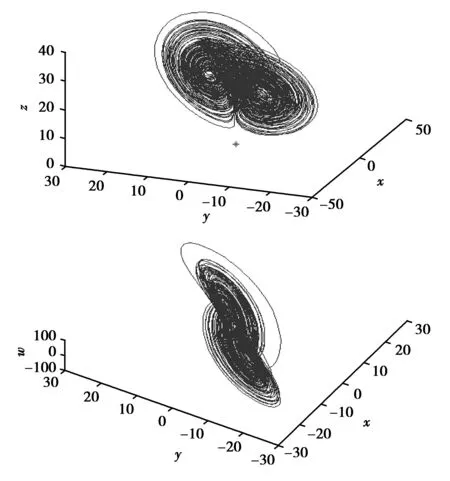
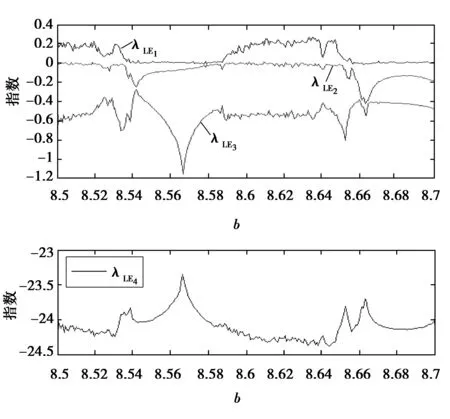
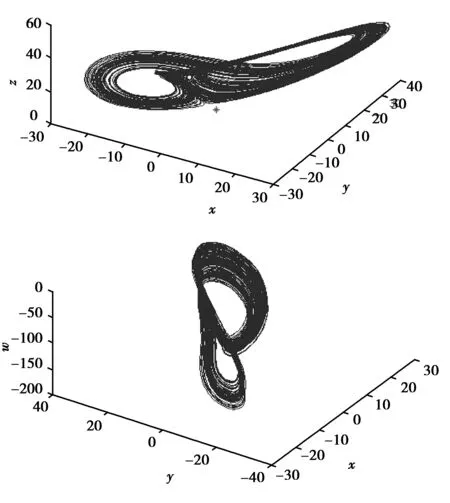
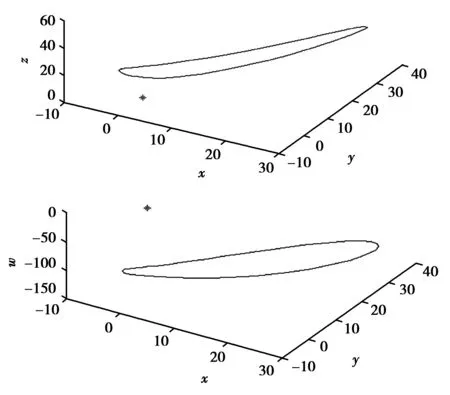
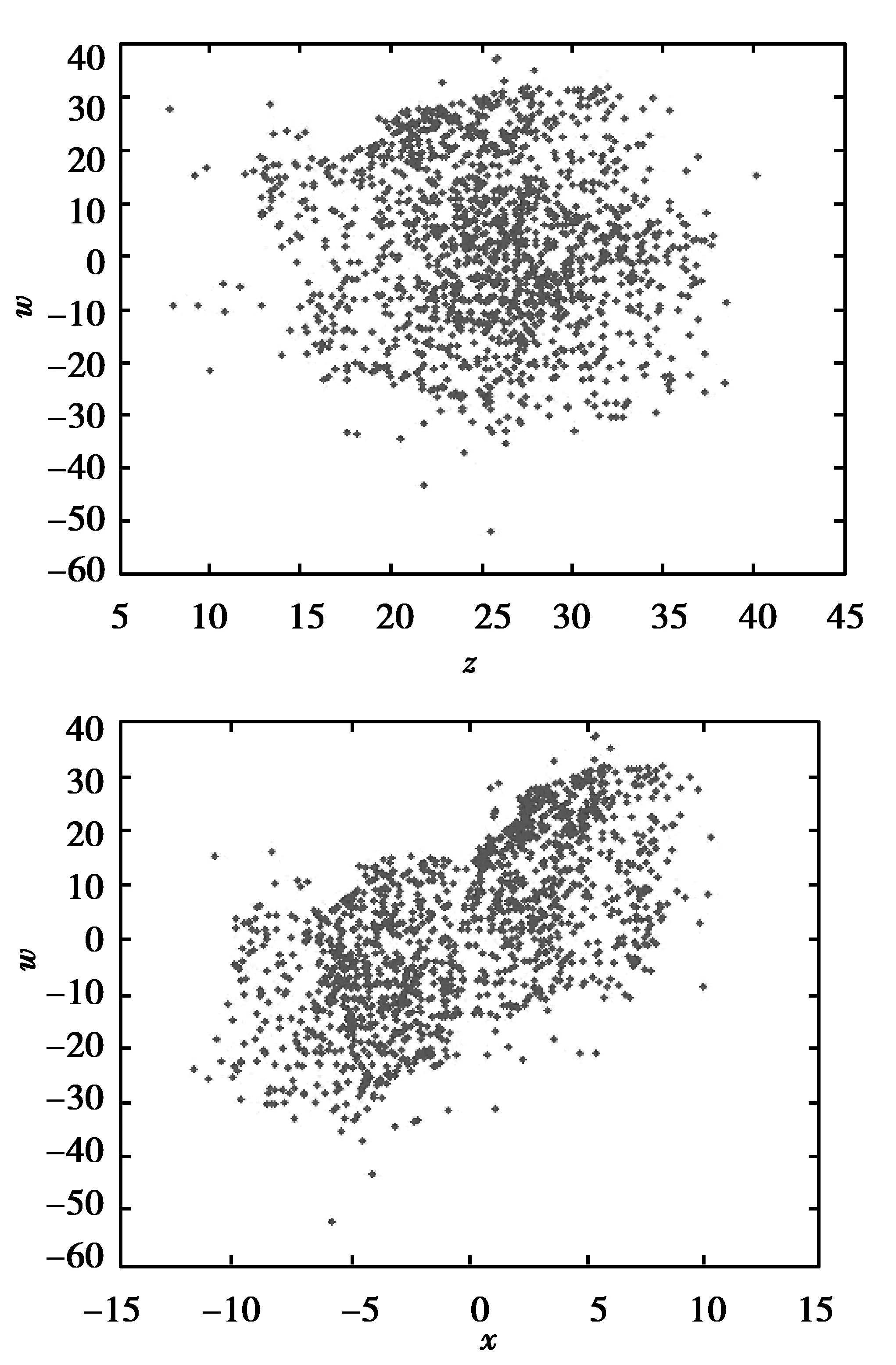
当满足条件c 当四维自治系统(2)的参数取(a,b,c,e,f)=(36,3,20,5,4.85),初始值为(0.1,0.1,0.1,0.1)时,系统(2)存在超混沌吸引子,其在三维空间中的投影和Poincaré映射图分别如图2和图3所示。 图2 系统(2)的超混沌吸引子相图在三维空间的投影:(a,b,c,e, f)=(36,3,20,5,4.85)Fig.2 Three-dimensional projections of hyperchaotic attractor of system (2):(a,b,c,e, f)=(36,3,20,5,4.85) 图3 系统(2)超混沌吸引子的Poincaré映射:(a,b,c,e, f)=(36,3,20,5,4.85)Fig.3 Poincaré mapping of hyperchaotic attractor of system (2):(a,b,c,e, f)=(36,3,20,5,4.85) 经过计算,此时系统(2)对应的Lyapunov指数为 根据混沌系统的Lyapunov维数定义: 进一步在上述参数下,系统(2)在平衡点O处的特征值为 因此O是一个双曲鞍点,有二维稳定流形和二维不稳定流形。 为方便,本文称系统(2)为四维超混沌Lü-like系统。 定理1 设△=a2+4f,a≠0,且b,c,f≠0,则超混沌系统(2)有下面结论: (Ⅰ) 当f>0时,超混沌系统(2)的平衡点O是双曲鞍点,且若b,c>0,则鞍点O有二维稳定流形和二维不稳定流形;若b>0,c<0,则鞍点O有三维稳定流形和一维不稳定流形;若b<0,c>0,则鞍点O有一维稳定流形和三维不稳定流形。 (Ⅱ) 当f<0,△≥0时,若a>0,b,c>0,则O是双曲鞍点,有三维稳定流形和一维不稳定流形;若a<0,b,c>0,则O是双曲鞍点,有一维稳定流形和三维不稳定流形;若a<0,b>0,c<0,则O是双曲鞍点,有二维稳定流形和二维不稳定流形;若a>0,b<0,c>0,则O是双曲鞍点,有二维稳定流形和二维不稳定流形;若a<0,b<0,c>0,则O是不稳定结点;若a>0,b>0,c<0,则O是稳定结点。 (Ⅲ) 当f<0,△<0时,若a>0,b,c>0,则O是鞍-焦点,有三维稳定流形和一维不稳定流形;若a<0,b,c>0,则O是鞍-焦点,有一维稳定流形和三维不稳定流形;若a<0,b>0,c<0,则O是鞍-焦点,有二维稳定流形和二维不稳定流形;若a>0,b<0,c>0,则O是鞍-焦点,有二维稳定流形和二维不稳定流形;若a<0,b<0,c>0,则O是不稳定结-焦点;若a>0,b>0,c<0,则O是稳定结-焦点。 证明 设J是系统(2)在任一点P(x,y,z,w)的Jacobi矩阵,则 特别可得系统(2)在平衡点O的Jacobi矩阵为 进一步得矩阵Jo的特征方程为 本文提出了一种基于改进的OCS调制方式,利用UFBG-AOTF光学生成多倍频可调谐毫米波的方法.在调制指数m=2.5π的条件下,最高倍频因子可达22.该方案通过控制UFBG-AOTF的声波频率实现FMF的线性调谐,仅使用一个DD-MZM,灵活、简单且成本较低,同时也降低了对振荡器及调制器的频率要求.此外,提高DD-MZM的调制系数能够实现更高倍频因子毫米波信号的产生.同时,对倍频因子为22时系统下行链路传输性能的分析表明,在只将基带数据信号调制到其中一个边带上的OCS改进方案中,信号可以进行长距离且性能更稳定的传输,有效避免了色散所导致的码元时移效应. (3) 因而系统在平衡点O处对应的特征值为 (Ⅰ) 当f>0时,λ3,4是异号的实根,因此O是双曲鞍点,且若b,c>0,则λ1,2是异号的实根,故鞍点O有二维稳定流形和二维不稳定流形;若b>0,c<0,则λ1,2是负的实根,故鞍点O有三维稳定流形和一维不稳定流形;若b<0,c>0,则λ1,2是正的实根,故鞍点O有一维稳定流形和三维不稳定流形。 (Ⅱ) 当f<0,△≥0时,若a>0,b,c>0,则λ1,2是异号的实根,特征值λ3,4与-a同号,故O是双曲鞍点,有三维稳定流形和一维不稳定流形;若a<0,b,c>0,则λ1,2是异号的实根,特征值λ3,4与-a同号,故O是双曲鞍点,有一维稳定流形和三维不稳定流形;同理可证(Ⅱ)中的其他情形结论成立。 (Ⅲ) 当f<0,△<0时,若a>0,b,c>0,则λ1,2是异号的实根,特征值λ3,4是一对共轭复数,且实部与-a同号,故O是鞍-焦点,有三维稳定流形和一维不稳定流形;若a<0,b,c>0,则λ1,2是异号的实根,特征值λ3,4是一对共轭复数,且实部与-a同号,故O是鞍-焦点,有一维稳定流形和三维不稳定流形。 同理可证(Ⅲ)中的其他情形结论成立。 下面给出新超混沌系统(2)的Hopf分岔的存在性定理。 定理2 (Hopf分岔的存在性) 若条件a=0,f<0成立,则当参数a发生变化并通过临界值a0=0时,系统(2)在平衡点O产生Hopf分岔。 证明 根据定理1的证明,可得特征方程(3)成立,设式(3)有一对纯虚根λ=±iω(ω∈R+),将虚根iω代入式(3)易知,当f<0 时,有 把a=a0=0代入式(3)可得 因此,当a=0,f<0成立时,Hopf分岔[12]的第一个条件满足。 再根据式(3)和f<0,可得 从而求得 因此,Hopf分岔[12]的第二个条件也满足,故系统(2) 存在Hopf分岔。 本节利用相图、Lyapunov指数及分岔图等工具,适当选取系统的参数,进一步研究系统(2)的超混沌、混沌及周期等复杂动力学行为。 当系统(2)的参数取 (a,b,c,e)=(36,3,20,5),f在区间[3.5,6.5] 变化时, 系统(2)存在唯一平衡点,此时对应的Lyapunov指数和分岔图分别如图4和图5所示。由图中可以知道,系统在f∈[3.5,6.5]整个变化过程中都是超混沌的,其吸引子的Lyapunov指数有2个正的。 图4 系统(2)的Lyapunov指数图:(a,b,c,e)=(36,3,20,5,), f∈[3.5,6.5]Fig.4 Lyapunov exponent of system (2):(a,b,c,e)=(36,3,20,5,), f∈[3.5,6.5] 特别选取参数: 可计算得对应的Lyapunov指数为 且DL=3.071 2。进一步,超混沌吸引子在三维空间中的投影如图6所示,由定理1知,唯一平衡点O是双曲鞍点,且有二维稳定流形和二维不稳定流形。 图6 系统(2)的超混沌吸引子的相图:(a,b,c,e, f)=(36,3,20,5,6.4)Fig.6 Phase portraits of hyperchaotic attractor of system (2):(a,b,c,e, f)=(36,3,20,5,6.4) 当系统参数取 (a,c,e,f)=(36,20,5,8),b在区间[8.5,8.7] 变化时,系统(2)有复杂的动力学行为,此时对应的Lyapunov指数和分岔图分别如图7和图8所示。 图7 系统(2)的Lyapunov指数图:(a,c,e, f)=(36,20,5,8),b∈[8.5,8.7]Fig.7 Lyapunov exponent of system (2):(a,c,e, f)=(36,20,5,8),b∈[8.5,8.7] 图8 系统(2)的分岔图:(a,c,e, f)=(36,20,5,8),b∈[8.5,8.7]Fig.8 Bifurcation diagram of system (2):(a,c,e, f)=(36,20,5,8),b∈[8.5,8.7] 由图7—8的数值分析,且通过仔细观察,可知系统(2)存在混沌吸引子和周期吸引子。 特别地选取参数: (a,b,c,e,f)=(36,8.598,20,5,8) 可得对应的Lyapunov指数为 这表明系统(2)有一个混沌吸引子,对应的相图如图9所示。 图9 系统(2)的混沌吸引子在三维空间投影:(a,b,c,e, f)=(36,8.598,20,5,8)Fig.9 Three-dimensional projections of chaotic attractor of system (2):(a,b,c,e, f)=(36,8.598,20,5,8) 由定理1知,唯一平衡点O是双曲鞍点,有二维稳定流形和二维不稳定流形。 特别地选取参数: (a,b,c,e,f)=(36,8.6674,20,5,8) 对应的Lyapunov指数为 表明系统(2)有一个周期吸引子,对应的相图如图10所示。 图10 系统(2)的周期吸引子在三维空间投影:(a,b,c,e, f)=(36,8.6674,20,5,8)Fig.10 Three-dimensional projections of periodic attractor of system (2):(a,b,c,e, f)=(36,8.6674,20,5,8) 由定理1知,唯一平衡点O是双曲鞍点,且有二维稳定流形和二维不稳定流形。 [1] LORENZ E N.Deterministic Non-periodic Flow[J].Journal of the Atmospheric Sciences,1963(20):130-141 [2] ROSSLER O E.An Equation for Hyperchaos[J]. Physics Letters A,1979(71):155-157 [3] CHEN Y M,YANG Q G.Dynamics of a Hyperchaotic Lorenz-type System[J].Nonlinear Dyn,2014(77):569-581 [4] CHEN Z Q,YANG Y,QI G Y.A Novel Hyperchaos System Only with One Equilibrium[J].Physics Letters A,2007(360):696-701 [5] XUE W,QI G Y,MU J J,et al.Hopf Bifurcation Analysis and Circuit Implementation for a Novel Four-Wing Hyperchaotic System[J].Chinese Physics B,2013(8):504-508 [6] MATSUMOTO T,CHUA L O,KOBAYASHI K.Hyperchaos:Laboralory Experiment and Numerical Confirmation[J].IEEE Transactions on Circuits and Systems,1986(11):1143-1147 [7] KAPITANIAK T,CHUA L O,ZHONG G Q.Experimental Hyperchaos in Coupled Chua’s Circuits[J].IEEE Transa-ctions on Circuits & Systems I-Fundamental Theory & Applications, 1994,41(7):499-503 [8] LI Y X,TANG W K S,CHEN G R.Hyperchaos Evolved from the Generalized Lorenz Equation[J].International Journal of Circuit Theory and Applications,2005,33(4):235-251 [9] YANG Q G, LIU Y J.A Hyperchaotic System from a Chaotic System with One Saddle and Two Stable Node-Foci[J].J Math Anal Appl,2009(36):293-306 [10] YANG Q G, ZHANG K M, CHEN G R.Hyperchaotic Attractors from a Linearly Controlled Lorenz System[J].Nonlinear Analysis:Real World Applications,2009(10):1601-1617 [11] LU J H, CHEN G R.A New Chaotic Attractor Coined[J].International Journal of Bifurcation and Chaos, 2002,12(3):659-661 [12] GUCKENHEIMER J, HOLMES P.Nonlinear Oscillations,Dynamical Systems and Bifurcation of Vector Field[M].Springer,NY,1983 责任编辑:李翠薇 Study on a4D Hyperchaotic Lü-like System Only with One Equilibrium ZHANG Yan-hong, YANG Qi-gui (School of Mathematical Science, South China University of Technology, Guangzhou 510640, China) Based on three-dimensional (3D) Lü chaotic system, and with the help of feedback control techniques, this paper reports a new 4D autonomous hyperchaotic system with five parameters and three nonlinear items, analyzes the dynamic properties of the system, as the new system has only one equilibrium, and studies the stability of corresponding equilibrium. Meanwhile the local dynamics such as Hopf bifurcation is rigorous derived; in addition, numerical analysis of phase trajectories, bifurcation and Lyapunov exponents verifies the existence of the hyperchaotic attractor, chaotic attractor and periodic attractor. Lü system; 4D hyperchaotic system; Lyapunov exponents; stability; Hopf bifurcation 10.16055/j.issn.1672-058X.2017.0003.010 2017-01-18; 2017-02-21. * 基金项目:国家自然科学基金(11671149);广东省自然科学基金(2014A030313256). 张艳红(1988-),女,河南太康人,硕士研究生,从事混沌动力学研究. **通讯作者:杨启贵(1965-),男,重庆市人,教授,博士,从事混沌动力学研究.E-mail:qgyang@scut.edu.cn. O127 A 1672-058X(2017)03-0049-07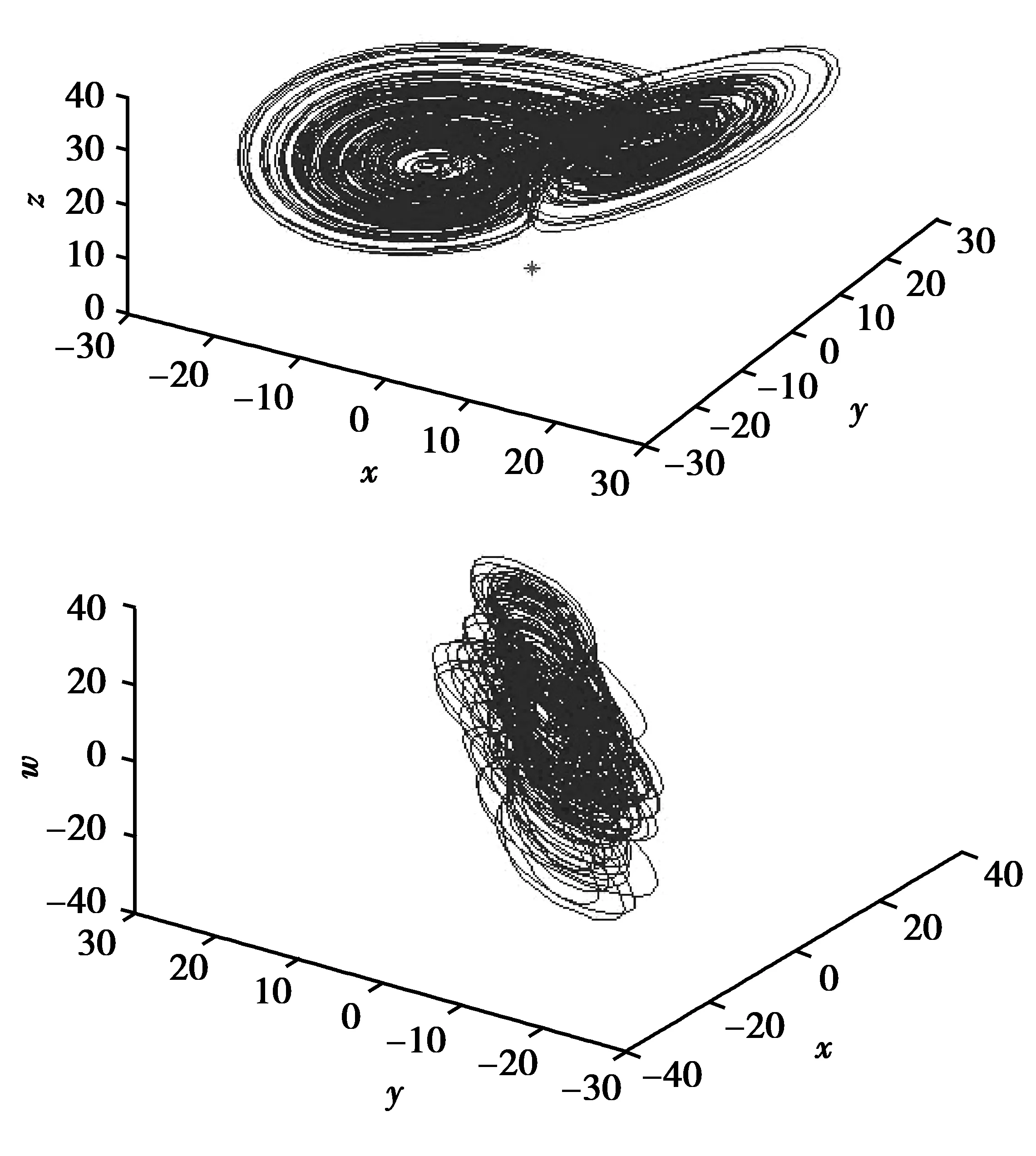
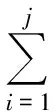
2 局部动力学性质
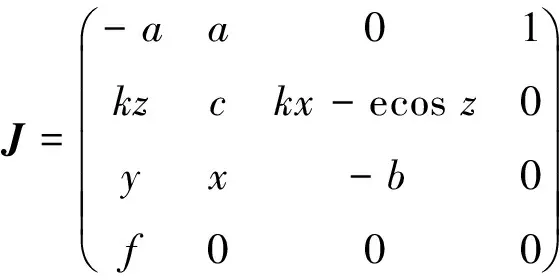
3 数值复杂动力学