基于ANSYS的高压交流电缆接头载流量确定方法*
2017-06-19刘刚王鹏宇王振华徐涛刘毅刚韩卓展
刘刚 王鹏宇 王振华 徐涛 刘毅刚 韩卓展
(1.华南理工大学 电力学院, 广东 广州 510640; 2.广州供电局有限公司输电管理所, 广东 广州 510310;3.广东电机工程学会电缆专委会, 广东 广州 510080)
基于ANSYS的高压交流电缆接头载流量确定方法*
刘刚1王鹏宇1王振华1徐涛2刘毅刚3韩卓展1
(1.华南理工大学 电力学院, 广东 广州 510640; 2.广州供电局有限公司输电管理所, 广东 广州 510310;3.广东电机工程学会电缆专委会, 广东 广州 510080)
为了实现接头载流量的准确计算,提出了一种基于ANSYS的高压交流电缆接头载流量确定方法.该方法以绝缘长期耐受温度为限制条件,利用接头轴向二维有限元仿真模型计算载流量.仿真结果表明,当对流散热环境和负荷都相同时,相同导体截面的电缆接头导体温度高于电缆本体的导体温度,接头的载流能力低于同导体截面电缆的载流能力.为验证仿真模型精度,设计了接头载流量实验平台,对不同负荷下110 kV电缆接头稳态温度分布进行了实测.仿真与实验结果的对比表明,当接头导体温度超过绝缘长期耐受温度时,应用接头轴向二维有限元仿真模型计算压接管处导体温度的误差不超过1.0%,仿真计算的准确度能够满足工程应用的需求.最后,采用二分法算得110 kV 630 mm2电缆接头载流量为1 220 A,比相同导体截面电缆本体在相同环境条件下的载流量减少了17.79%.研究结果表明:采用接头轴向二维有限元仿真模型计算载流量是可行的.
高压电缆接头;载流量;二维有限元仿真;轴向传热;稳态实验
随着城市化进程的不断加快,现有电缆线路输电压力日益增大,实现电缆的动态增容已成为解决矛盾的必要措施[1-3].传统方法评定电缆全线载流量时只考虑电缆本体的载流能力,假定电缆附件运行在相同或更低的温度条件下[4-5].但在电缆线路实际运行过程中,电缆接头导体温度往往高于电缆本体导体温度,传统的电缆线路载流量评定方法精确度较低.由统计数据可知,电缆附件事故占到电缆事故的70%,电缆接头已成为电力电缆绝缘最薄弱的关键点[6].因此,为评估电缆接头载流能力,从而为电缆接头易过热损坏的解决和电缆全线载流量的提升提供支持,对接头温度场分布的研究迫在眉睫.电缆接头运行环境复杂多变,利用有限元仿真方法可以很好地实现对不同条件下接头温度场分布的求解.
国内外学者对电缆接头载流量的早期研究多集中在对接头等效热网络的建立和求解,以热路的形式表征电缆接头内热量的传递过程,利用数学方法求解热网络即可得到电缆接头的载流量[7-9].文献[10]中搭建了电缆接头三维暂态热路模型,并实现了对接头导体温度的求解,但接头导体温度的求解精度受接头分段数的制约,随着分段数的增加求解精度提高,而接头热路的求解难度却大大提高;且接头实际结构复杂,分段后各部分热物性参数的准确确定也较难实现,这和工程实际应用的需求是相悖的,因此等效热路法的使用受到了限制.
随着计算机技术的快速发展,数值计算方法越发成熟,现有的有限元分析工具已具有较强的计算能力和良好的后处理能力,利用数值计算方法求解电缆接头温度场分布的使用日益受到重视[11-13].相比于热网络分析方法,利用数值计算模型求解电缆接头载流量大大减小了建模的复杂度,改善了求解质量.文献[14]中采用数字温度传感器测量冷缩预制件表面温度作为原始数据,构建中间接头的径向温度场仿真模型计算线芯的稳态温度.文献[15]中结合传热学理论和有限元法,构建电缆接头径向稳态温度场,分析了接头导体温度和表面温度的对应关系.文献[16]中采用有限元分析法计算电缆接头额定载流量,以400 kV电缆接头为例,搭建轴对称二维有限元仿真模型,采用灵敏度分析验证模型简化的可行性,并将二维仿真模型扩展为三维仿真模型,模拟接头真实运行条件下热场分布特点.
国内外学者对电缆接头热场的研究多集中于接头径向热场分析,而对电缆接头轴向热场分析和相应的实验验证有待进一步研究.文中以110 kV预制式直通接头为例,通过ANSYS建立了电缆接头的二维轴向有限元仿真模型,分析了稳态时电缆接头的温度分布特点,并通过高压电缆接头载流量实验,验证和优化了仿真模型;最后利用二分法实现了电缆接头载流量的准确计算,达到了评定电缆接头载流能力的目的.
1 高压电缆接头轴向二维有限元仿真
利用结构复杂的三维仿真模型来解决电缆接头温度场分布的求解从而实现对接头载流量的评估是低效且浪费时间的.电缆本体和接头主体主要组成部分为轴对称结构,且接头少量非对称结构对电缆导体温度影响很小[17].因此,在求解接头数值计算模型时,可认为接头沿半径方向具有各向同性,对电缆接头稳态温度场分布的求解可等效为2维稳态导热问题,大幅度提高了求解的效率.
以110 kV 630 mm2交联聚乙烯绝缘预制式直通接头为例,说明接头二维轴向仿真模型的建立和求解过程,其真实结构如图1所示.
为了能够搭建接头二维轴向仿真模型,有必要对接头的几何结构做出一系列假设:将接头铜保护壳等效为圆柱体结构,忽略顶部接地柱的影响;用等效半径来描述电缆的波纹铝护套;考虑到接头中微小结构对接头整体热场分布的影响可以忽略不计,将其从接头几何结构中移除[17].则可在ANSYS中建立电缆接头沿轴向的二维几何模型,如图2所示.电缆及接头各层结构的结构参数和材料导热系数如表1和2所示.

图1 110 kV预制式直通接头

图2 接头轴向二维几何模型

结构材料直径/mm导热系数/(W·m-1·K-1)导体铜30401.00导体屏蔽聚烯烃330.38导体绝缘交联聚乙烯670.40接头主绝缘乙丙橡胶2600.25PVC防水带PVC2610.1667密封填充剂环氧树脂密封胶2700.50保护铜壳铜272401.00热缩管聚烯烃2740.38

表2 电缆本体结构参数
1.1 电缆接头的数学模型
对于电缆任何区域,按照能量守恒定律,在任一时间间隔内有以下热平衡关系:导入区域的总热流量与区域内热源的生成热之和等于导出区域的总热流量与区域热力学能的增量之和.电缆接头稳态时能量守恒方程为
K·θ=Q
(1)
式中,矩阵K为由热传导、对流换热和热辐射组成的传导矩阵,矩阵θ为节点温度向量,矩阵Q为节点热流密度向量.矩阵K、θ和Q可通过ANSYS,根据模型几何尺寸、热特性和施加边界条件生成.
传热学数值算法中提出了3类热场边界条件:第1类边界为已知边界温度为固定常数;第2类边界为已知边界法向热流密度;第3类边界为对流边界条件为已知对流换热系数和流体温度[18].
第1类边界满足:
(2)
第2类边界满足:
(3)
第3类边界满足:
(4)

求解电缆接头的稳态温度分布等价于求解含有内在热源的二维热传导问题,其热传导稳态控制方程为

(5)
式中,qv为体积产热率.
1.2 边界条件的设定与求解
电缆接头在实际运行中环境条件复杂多变,其边界温度及边界热流密度难以准确确定,不适合采用第1类和第2类边界条件求解数值计算模型;且电缆接头多敷设于电缆沟或隧道内,其周围空气流速小于0.15 m/s,属于自然对流,因此文中采用第3类边界条件求解数值计算模型,取自然换热系数为7.5 W/(m·K),空气温度为25.0 ℃[18-19].
电缆接头内热源主要分为3类:导体产生的焦耳热、绝缘中介质损耗和铝护套中的环流损耗.绝缘中介质损耗和铝护套中的环流损耗在热源中所占比例很小,可以忽略其对接头内温度分布的影响.电缆接头的导体产热率为

(6)
式中:Q为导体的面产热率;r为导体半径;I为导体加载的电流;R为导体单位长度交流电阻,R可由IEC标准计算求得:
R=R0[1+α20(θ-20)](1+YS+YP)
(7)
式中,R0为导体20 ℃时导体的直流电阻,α20为每一绝对温度下20 ℃时铜的温度系数,θ为导体稳态温度,YS为集肤效应因数,YP为领进效应因数.
不同载荷水平下稳态时电缆接头导体的最高温度是不同的,因此导体稳态时的交流电阻是电流的函数,若将其视为定值则会给仿真结果带来误差.文中采用迭代法计算不同载荷能力下电缆接头的最高温度,从而计算出导体产热率,得出接头的稳态温度分布.具体步骤如下:
步骤1 求出导体温度θ1为90 ℃时的交流电阻R1和导体产热率Q1,将导体产热率Q1和空气中自然对流散热条件作为加载条件代入到接头轴向二维有限元仿真模型中.
步骤2 求解模型,在得出的温度分布云图中找出电缆接头的最高温度θ2,并重新计算导体交流电阻R2和产热率Q2.
步骤3 将导体产热率Q2和空气中自然对流散热条件作为加载条件再次代入模型求解出新的接头最高温度θ3,并重新计算导体交流电阻和产热率.如此反复迭代直至相邻两次迭代计算温度差值满足精度要求,则认为迭代收敛,此时的温度即为接头稳态时导体的最高温度,并得到该条件下稳态温度场的分布.
由迭代法计算可得:接头加载电流1 000 A时导体产热率为57 393.7 W/m2,接头加载电流1 250 A时导体产热率为89 677.6 W/m2,接头加载电流1 484 A时导体产热率为126 395.6 W/m2.
1.3 仿真结果及分析
对接头二维仿真模型求解,得到不同负荷下电缆接头及附近本体稳态温度分布云图,如图3所示.
由图3可以看出:
1)电缆接头加载电流达到稳态后,沿接头轴向存在温度分布梯度.接头压接管处温度最高.从接头压接管到2 m外电缆本体,导体稳态温度呈先下降后增长再下降的变化趋势,导体温度在铜壳端口附近出现极小值点.
2)当电缆接头加载1 250 A电流达到稳态时,接头压接管处温度为92.4 ℃,已超过交联聚乙烯绝缘的长期耐受温度,而此时电缆本体导体稳态温度只有76.2 ℃,仍远低于绝缘长期耐受温度,电缆本体导体未得到有效利用.
3)当电缆接头加载1 484 A电流达到稳态时,电缆本体导体温度达到绝缘长期耐受温度,而此时接头压接管处温度高达114.9 ℃,远超绝缘长期耐受温度.由老化原理可知,电缆若长期运行在满负荷条件下,将加速电缆接头绝缘的热老化,接头使用寿命会大大缩短.

图3 不同负荷时电缆接头及附近本体的稳态温度分布云图Fig.3 Steady-state temperature distribution of cable joint and cable body nearby at different currents
表3给出了不同载荷下电缆接头导体稳态温度的仿真计算结果.可以看出,在同等自然对流散热环境和同等负荷下,相同导体截面的电缆接头导体温度高于电缆本体的导体温度,而二者的载流能力都取决于XLPE绝缘长期运行的最高耐受温度(90 ℃)[20].由此可知,电缆接头的载流能力低于同导体截面电缆的载流能力.

表3 电缆接头导体稳态温度
2 高压电缆接头温升实验
为研究接头稳态时的温度分布特点,为接头二维有限元仿真模型的验证提供可靠温度数据,设计了110 kV 630 mm2电缆接头稳态温升实验,实验系统如图4所示.实验系统分为室内和室外两个部分,室内部分包括大电流自动升流负载实验系统、升流器、无功补偿电容器,室外部分为实验负载.
实验电缆放置在盖板的电缆沟内,无直射日照的影响,且实验时环境温度和湿度变化不大,可近似等效为恒温恒湿环境.电缆沟内空气流速小于0.15 m/s,属于自然对流.

图4 实验系统示意图
以电缆接头压接管中点为0 m基准,在距离压接管中点3.50 m范围内,每隔一定距离在电缆导体表面设置1个测温点,如图5所示.测温传感器采用热电偶,为提高温度测量的精确度,在同一测温点的不同方向分别布置3个热电偶.

图5 测温点布置示意图
由仿真结果可知,电缆加载1 484 A阶跃电流达到稳态时,接头处运行温度将远超绝缘的长期耐受温度,对接头绝缘的伤害较大.因此,通过升流变压器,只对电缆接头加载1 000 A、1 250 A阶跃电流直至稳态,获得这段范围内接头及附近本体导体的稳态温度实验数据分布,如图6和表4所示.
结合图6和表4可以看出:

图6 阶跃电流作用下接头轴向稳态温度分布曲线
Fig.6 Steady axial temperature profiles in the single-stage step current role
表4 不同负荷下电缆接头轴向温差对比
Table 4 Temperature difference contrast of cable joint under different loads
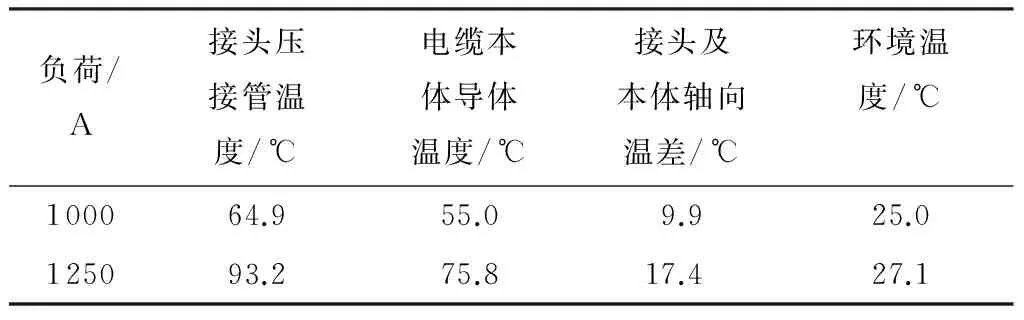
负荷/A接头压接管温度/℃电缆本体导体温度/℃接头及本体轴向温差/℃环境温度/℃ 100064.955.09.925.0125093.275.817.427.1
1)稳态时电缆接头压接管处导体温度最高.分析产生这种现象的原因,需从产热和散热两个方面出发.接头内采用压接管连接两段导体,压接处引入了接触电阻,增加了接头内的发热,且接触电阻会随着温度的升高而增大,进一步提高了压接管处导体的温度;电缆接头制作工艺要求较高,结构尺寸远大于电缆本体,散热条件较差.
2)稳态时电缆接头及附近本体间存在轴向温度分布,沿压接管至电缆本体,导体温度呈先下降后增长再下降的变化趋势,在铜壳端口附近出现一个极小值点.分析其原因在于,保护铜壳端口处电缆剥切了铝护套,与空气对流散热条件良好,此时散热对电缆导体的温度起到了主导作用.
综合实验数据分析可知,在同等负荷和同等敷设环境下,电缆接头导体温度高于同导体截面电缆本体的导体温度,则电缆接头的载流能力低于同导体截面电缆本体的载流能力.实验结果和仿真结果一致,验证了接头轴向二维仿真模型的正确性.
3 讨论
对比分析相同载荷、相同环境条件下的电缆接头温度的仿真和实验结果,如图7所示.
由图7可知,基于电缆接头轴向二维仿真模型得出的接头轴向温度分布曲线和实验实测的温度分布曲线趋势相同,都呈现先下降后增长再下降的趋势,其中仿真求得的压接管温度低于实测值,其他测温点的仿真结果均高于实测值,有一定误差.分析接头轴向二维仿真模型产生误差的原因如下:

图7 不同负荷下接头仿真和实验结果对比
Fig.7 Comparison of simulated and experimental results of joint under different loads
1)接头铜网屏蔽层属于多孔结构,孔隙和细铜丝混合的导热系数无法准确设定;半导电层、硅橡胶等有机多分子材料的导热系数随温度的变化而变化,且各厂家使用的原材料特性存在一定差异,其导热系数也无法准确设定.
2)计算接头热源时,只考虑了导体的焦耳热,忽略了绝缘中介质损耗和铝护套中的环流损耗.
3)仿真时设定电缆接头边界条件均匀且恒定,而实际运行过程中,电缆接头表面的边界条件并非均匀,接头各处的空气温度和对流速度不完全相同,且随时间的变化而变化.
以接头温度实测值为基准,对接头轴向二维仿真模型误差分析如表5所示.由表5可知,电缆在1 000 A阶跃电流作用下,仿真误差最大值出现在距离压接管中线2.41 m处的电缆本体,最大为3.6%;电缆在1 250 A阶跃电流作用下,仿真误差最大值出现在距离压接管中线0.96 m处的接头铜壳端口附近,最大为9.8%.当接头导体温度超过绝缘长期耐受温度时,应用接头轴向二维仿真模型计算压接管处导体温度的误差很小,不超过1.0%,计算结果准确度能够满足工程应用的需求.可见,接头轴向二维仿真模型可以实现较为准确的接头载流量计算.

表5 接头轴向二维仿真模型误差
4 高压电缆接头载流量计算实例
由上文分析可知,高压电缆接头的载流量不同于相同截面的电缆本体,现有的IEC标准不适用于设计电缆接头的载流量.在接头轴向二维有限元仿真模型精度已得到验证的前提下,文中提出一种以绝缘长期耐受温度为限制条件,利用接头轴向二维有限元仿真模型计算接头载流量的方法.
计算电缆接头载流量时导体产热率仍由式(6)给出,式中,R为电缆接头导体温度达到绝缘长期耐受温度时的单位长度导体交流电阻.文中以110 kV 630 mm2电缆为例,针对接头轴向二维有限元仿真模型,以绝缘长期耐受温度为限制条件,采用二分法计算得到电缆接头的载流量为1 220 A[21].由上文可知,相同截面的电缆本体载流量为1 484 A.在相同环境条件下,相比于电缆本体,电缆接头载流量减少了17.79%,进一步验证了在同等自然对流散热环境下电缆接头的载流能力低于同导体截面电缆的载流能力这一结论的正确性.
5 结论
文中搭建了接头轴向二维有限元仿真模型,设计了接头稳态温升实验,通过仿真和实验分析得到如下结论:
1)稳态时电缆接头及附近本体间存在轴向温度分布,压接管处导体温度最高,沿压接管至电缆本体,导体温度呈先下降后增长再下降的变化趋势.在同等自然对流散热环境和同等负荷下,相同导体截面的电缆接头导体温度高于电缆本体的导体温度,电缆接头的载流能力低于同导体截面电缆的载流能力.电缆本体导体温度达到90 ℃时,电缆接头处导体温度已远超接头内电缆XLPE绝缘长期耐受温度,加速了接头绝缘的热老化,影响接头使用寿命,危害线路的安全运行.
2)仿真和实验结果一致,验证了接头轴向二维有限元仿真模型的正确性.当接头导体温度超过绝缘长期耐受温度时,应用接头轴向二维仿真模型计算压接管处导体温度误差不超过1.0%,计算结果准确度能够满足工程应用的需求,接头轴向二维仿真模型可以实现较为准确的接头载流量计算.
3)针对接头轴向二维有限元仿真模型,采用二分法计算得到110 kV 630 mm2电缆接头的载流量为1 220 A,比相同导体截面电缆本体在相同环境条件下的载流量减少了17.79%,进一步验证了在同等自然对流散热环境下电缆接头的载流能力低于同导体截面电缆的载流能力这一结论的正确性.
[1] 吴畏,杨博麟,王轶群,等.电力电缆及其接头运行温度监测技术研究 [J].电线电缆,2011(4):42-44. WU Wei,YANG Bo-lin,WANG Yi-qun,et al.Research of techniques for monitoring the operation temperature of the power cable and cable joints [J].Electric Wire & Cable,2011(4):42-44.
[2] 李应宏,雷成华,刘刚.基于材料导热系数的单芯高压电缆导体温度动态分析 [J].华东电力,2011,39(8):1300-1303. LI Ying-hong,LEI Cheng-hua,LIU Gang.Dynamic analysis of conductor temperature of the high voltage single-core cable based on thermal conductivity [J].East China Electric Power,2011,39(8):1300-1303.
[3] LI Y,WOUTERS P,WAGENAARS P,et al.Temperature dependent signal propagation velocity:possible indicator for MV cable dynamic rating [J].IEEE Translation on Dielectrics and Electrical Insulation,2015,22(2):665-672.
[4] NEHER J H,MCGRATH M H.The calculation of the temperature rise and load capability of cable systems [J].Power Apparatus and Systems,Part III.Transactions of the American Institute of Electrical Engineers,1957,76(3):752-764.
[5] 江日洪.交联聚乙烯电力电缆线路 [M].北京:中国电力出版社,2009:92-94.
[6] 刘辉.电缆故障诊断理论与关键技术研究 [D].武汉:华中科技大学,2012:32-33.
[7] 刘刚,雷鸣,阮班义,等.考虑轴向传热的单芯电缆线芯温度实时计算模型研究 [J].高电压技术,2012,38(8) :1877-1883. LIU Gang,LEI Ming,RUAN Ban-yi,et al.Model research of real-time calculation for single-core cable temperature considering axial heat transfer [J].High Voltage Engineering,2012,38(8):1877-1883.
[8] 雷鸣,刘刚,赖育庭,等.采用Laplace方法的单芯电缆线芯温度动态计算 [J].高电压技术,2010,36(5):1150-1155. LEI Ming,LIU Gang,LAI Yu-ting,et al.Dynamic calculation of core temperature of single core cables using Laplace method [J].High Voltage Engineering,2010,36(5):1150-1155.
[9] 雷成华,刘刚,李钦豪.BP神经网络模型用于单芯电缆导体温度的动态计算 [J].高电压技术,2011,37(1):184-189. LEI Cheng-hua,LIU Gang,LI Qin-hao.Dynamic calcu-lation of conductor temperature of single-cable using BP neural network [J].High Voltage Engineering,2011,37(1):184-189.
[10] NAKAMUAR S,MOROOJKA S,KAWASAKI K.Con-ductor temperature mnitoring mystem in underground power transmission XLPE cable joints [J].IEEE Tran-sactions on Power Delivery,1992,7(4):1688-1697.
[11] 雷鸣,刘刚,邱景生,等.电缆线芯温度的非线性有限元法实时计算 [J].电网技术,2011,35(11):164-168. LEI Ming,LIU Gang,QIU Jing-sheng,et al.Real-time core temperature calculation of single-core cable by nonlinear finite element method [J].Power System Technique,2011,35(11):164-168.
[12] 吴畏,汪讽,黄智伟,等.110 kV高压电力电缆中间接头电场-温度场的仿真分析 [J].传感器与微系统,2011,30(8):15-17. WU Wei,WANG Feng,HUANG Zhi-wei,et al.Simula-tion analysis of electric-thermo field of 110 kV power cable joint [J].Transducer and Microsystem Technolo-gies,2011,30(8):15-17.
[13] WEEDY B M,PERKINS J P.Steady-state thermal analysis of a 400 kV cable through joint [J].Proceedings of the IEEE,1967,114(1):109-115.
[14] 常文治,韩筱慧,李成榕,等.阶跃电流作用下电缆中间接头温度测量技术的实验研究 [J].高电压技术,2013,39(5):1156-1162. CHANG Wen-zhi,HAN You-hui,LI Cheng-rong,et al.Experimental study on cable joint temperature measure-ment technology under step current [J].High Voltage Engineering,2013,39(5):1156-1162.
[15] LIN Shan-ming,HU Wan-qing.Theoretical research on temperature field of power cable joint with FEM [C]∥Proceedings of 2012 International Conference on System Science and Engineering.Dalian:IEEE,2012:564-567.
[16] PILGRIM J Al.An investigation of thermal ratings for high voltage cable joints through the use of 2D and 3D finite element analysis [J].IEEE Dielectrics and Electrical Insulation Society,2008,1089(84):543-546.
[17] PILGRIM James A,SWAFFIELD David J S,LEWIN Paul L,et al.Assessment of the impact of joint bays on the ampacity of high-voltage cable circuits [J].IEEE Transactions on Power Delivery,2009,24(3):1029-1036.
[18] 王磊,刘国建,严浩军,等.基于有限元分析法的电缆中间接头温升仿真研究 [J].上海电力学院学报,2014,30(5):428-432. WANG Lei,LIU Guo-jian,YAN Hao-jun,et al.Study of mechanism of temperature rise on power cable joint [J].Journal of Shanghai University of Electric Power,2014,30(5):428-432.
[19] 郝艳捧,曾彤,阳林,等.高压直流电缆终端载流量确定方法 [J].电网技术,2015,39(9):2519-2525. HAO Yan-peng,ZENG Tong,YANG Lin,et al.The determination method of steady-state current-carrying capacity of HVDC cable terminal [J].Power System Technology,2015,39(9):2519-2525.
[20] 马国栋.电线电缆载流量 [M].北京:中国电力出版社,2003:54-56.
[21] 王有元,陈仁刚,陈伟根,等.基于有限元法的 XLPE电缆载流量计算及其影响因素分析 [J].重庆大学学报,2010,33(5):72-77. WANG You-yuan,CHEN Ren-gang,CHAN Wei-gen,et al.Calculation of the ampacity of XLPE power cable based on FEM and analysis of the influential factors [J].Journal of Chongqing University,2010,33(5):72-77.
Determination Method of Current-Carrying Capacity of HVAC Cable Joint Based on ANSYS
LIUGang1WANGPeng-yu1WANGZhen-hua1XUTao2LIUYi-gang3HANZhuo-zhan1
(1.School of Electric Power, South China University of Technology, Guangzhou 510640, Guangdong, China;2.Transmission Management, Guangzhou Power Supply Bureau Ltd., Guangzhou 510310, Guangdong, China;3.Guangdong Society for Electrical Engineering, Guangzhou 510080, Guangdong, China)
In order to accurately calculate the current-carrying capacity of HVAC (High-Voltage AC) cable joints, a method based on ANSYS, which employs the two-dimension finite element simulation model of the joint in axial direction and takes the insulation’s long-term tolerating temperature as the constraint condition, is presented, and, a simulation is performed, finding that, under the same natural convection and load conditions, the temperature of the joint conductor is higher than that of the cable conductor with equal sectional area, while the current-carrying capacity of the cable is better than that of the joint. Then, in order to verify the precision of the simulation model, an experimental platform to measure the joint’s current-carrying capacity is established, and the practical steady-state temperature distribution of the 110 kV cable joint under different loads is measured. Moreover, a comparative analysis is carried out between the simulated and the experimental results, finding a 1.0% error of the cable joint conductor’s temperature calculated with the finite element simulation model when the temperature exceeds the insulation’s long-term tolerating temperature, which means that the accuracy of the calculation results may satisfy the demand of engineering application. Finally, a current-carrying capacity of 1 220 A is obtained for the 10 kV 630 mm2cable joint by using the dichotomy, which is 17.79% less than that of the cable body with the same conductor cross section under the same environmental conditions. Thus, it is concluded that the proposed two-dimension finite element simulation model of the joint in axial direction is feasible in calculating the current-carrying capacity.
high-voltage cable joint; current-carrying capacity; 2D finite element simulation; axial heat conduction; steady-state experiment
2016-07-14
国家高技术研究发展计划(863计划)项目 (2015AA050201) Foundation item: Supported by the National High-Tech R&D Program of China(863 Program)(2015AA050201)
刘刚(1969-),男,博士,副教授,主要从事过电压及其防护、电力设备外缘研究.E-mail:liugang@scut.edu.cn
100 0-565X(2017)04-0022-08
TM 726.4
10.3969/j.issn.1000-565X.2017.04.004
