含分布式电源的改进配电网随机潮流计算*

黄煜 徐青山 刘建坤 卫鹏

(1.东南大学 电气工程学院， 江苏 南京 210096； 2.江苏省 电力试验研究院有限公司， 江苏 南京 210003)

含分布式电源的改进配电网随机潮流计算*

黄煜1徐青山1刘建坤2卫鹏2

(1.东南大学 电气工程学院， 江苏 南京 210096； 2.江苏省 电力试验研究院有限公司， 江苏 南京 210003)

随着分布式电源(DG)在配电网中所占比重的不断上升，系统面临不确定性增大、网架结构改变等问题的挑战，常规的潮流计算无法应对电网中存在的大量不确定因素.针对这一情况，文中提出一种基于帝国主义竞争算法(ICA)的配电网随机潮流.该方法可以方便地考虑各类拓扑结构、不同DG渗透率以及多个约束条件的复杂网络，且具有良好的收敛性.为了提高算法的寻优能力和收敛速度，在ICA基础上引入克隆进化算子.对改进的IEEE-33配电系统进行随机潮流计算，并与蒙特卡罗仿真法(MCS)比较.结果表明，所提方法具有较高的计算精度和实用价值.

随机潮流；智能配电网；分布式电源；帝国主义竞争算法；克隆进化

分布式发电(DG)是解决当前能源危机和环境污染问题的有效手段，随着单位电能生产成本的不断降低和政策的大力支持，含分布式电源的微网将是未来智能配电网的重要组成部分.由于可再生能源(如风能、太阳能等)以及负荷功率具有很大的不确定性，微网的运行控制将面临新的挑战.

潮流计算是电力系统运行分析和规划设计的基础，常规潮流方法如适合辐射型网络的前推回代法和环状结构的N-R法都无法全面反映系统不确定因素的影响[1]，并且大量DG的接入改变了原来配电网的拓扑结构(由纯辐射型变为弱环型)，使得单一的潮流算法具有很大的局限，因此研究适应未来智能配电网特点的潮流计算方法具有重要意义.

随机潮流(PLF)由Borkowska于1974年在文献[2]中首次提出，它将各种不确定因素作为输入变量，通过概率统计的手段得到系统稳态运行的宏观统计信息.目前，随机潮流的计算方法大致可分为3类[3]：模拟法、近似法和解析法.其中以蒙特卡罗仿真(MCS)为代表的模拟法最为基础[4].文献[5]中在MCS基础上引入负荷的k-均值聚类模型，可以有效缩减样本数量.文献[6]中采用Copula函数和拉丁超立方采样的方法，既考虑了输入变量之间的相关性，又提高了采样效率.近似法如点估计法(PEM)、一次二阶矩法(FOSMM)等可以有效弥补MCS计算规模大、耗时长的缺陷[7-8].文献[9]中提出一种计及变量相关性的改进型两点估计法来解决随机最优潮流问题，并与MCS所得结果和耗时进行比较.解析法一般由非线性潮流方程的简化和卷积运算两部分构成，文献[10]中采用交流线性化模型并结合半不变量和Gram-Charlier级数展开直接求得输出变量的概率分布(CDF).文献[11]中拓展了解析法的适用范围，通过Von Mises[12]理论求随机变量离散部分的分布，可以考虑发电机停运、线路故障等突发状况.对于系统中存在约束条件的一类问题，基于启发式算法的PLF具有一定优势.比如文献[13]中的混沌粒子群优化算法(PSO)用于新能源接入下的无功优化配置、文献[14]中的蛙跳算法结合MCS求解考虑网络约束的配电网三相潮流.

文中提出一种适用于配电网的改进帝国主义竞争算法(ICA)，该算法能反映大量DG接入下系统的不确定性，并且完全不受配电网拓扑结构(纯辐射型、纯环型或者弱环型)改变以及各种约束条件的影响.在ICA基础上引入克隆进化算子，以加快算法的收敛速度.对IEEE33节点系统的测试结果验证了所提方法的准确性、有效性和实用性.

1 系统随机模型

1.1 负荷随机模型

在传统潮流中，负荷功率都是作为常数处理，其值与时间和气候有关.实际负荷波动及预测结果具有很大的不确定性，可以看作随机变量，用正态分布近似描述[15].有功和无功功率P、Q的概率密度函数(PDF)分别为

(1)

式中，μP、σP和μQ、σQ分别为有功和无功功率的期望值和方差.

1.2 风力发电系统随机模型

风电机组的出力主要取决于风速，风速具有天然波动性.文献[16]中证明了双参数Weibull函数可用来拟合中长期的风速分布，其PDF表示如下：

(2)

式中，v为风速,k和c分别为Weibull分布的两个参数.将式(2)产生的风速序列代入式(3)的风机输出特性表达式，可以求出风力发电机有功出力的概率分布:

(3)

式中，PR为风机的额定功率,vR、vin和vout分别为额定风速、切入风速和切出风速.

1.3 太阳能光伏发电系统随机模型

太阳辐射强度和气温是影响光伏(PV)发电系统输出功率的主要因素，文中假设两者均服从正态分布.以辐射强度GSTC=1 000W/m2、电池板表面温度Tr=25 ℃作为标准状态，则任意状态下PV系统的输出功率有如下表达式：

(4)

式中，PSTC为标准状态PV系统的额定功率，GING、GSTC为实际和标况下的辐射强度，κ为最大功率温度系数，Tc和Tr分别为实际和参考温度.

2 配电网随机最优潮流模型

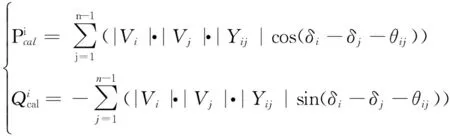
(5)

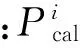
为了考虑负荷的不确定性，文中用正态分布拟合每个负荷节点功率，其中期望值等于平均功率[20]，最大有功和无功的变化率ΔP、ΔQ满足：

(6)

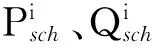
配电网中接入的DG可以看作是负的节点负荷，相应的风机及分布式光伏的有功随机模型见式(2)-(4).假设风机均采用恒功率因数控制，无功与有功之间的功率因数角φ恒定，而光伏输出无功为0，则节点i的计划功率修正为

(7)

(8)

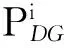
所提算法将未知量定义为输入向量x=[V1,V2,…,δ1,δ2,…]，其值随着ICA的每次迭代而更新.通过输入向量x，可以求得每个节点(除平衡节点)计算功率与计划功率之差，记为适应度函数F.目标函数Z为各节点适应度函数Fi之和.

min：{Z=sum(Fi)}

(9)

(10)

FPi和FQi如下：

(11)

(12)

式中，FPi包括了PQ和PV节点，而FQi只含PQ节点.用ICA求解目标函数的最小值，并要保证各节点的电压幅值和相角在约束范围之内.

|Vi,min|<|Vi|<|Vi,max|

(13)

δi,min<δi<δi,max

(14)

3 基于克隆进化的改进ICA

3.1 ICA原理

帝国主义竞争算法是由Atashpaz-Gargari和Lucas受帝国主义殖民竞争机制启发于2007年提出的一种进化算法[17].ICA首先随机构造出一系列国家，根据势力大小划分为帝国主义国家和殖民地两类，每个国家可以看作是由政治经济特征如文化、语言、宗教等构成的一个集合.完整的ICA步骤包括：初始帝国的产生、同化、革命、交换帝国和殖民地的位置、帝国的竞争及消亡.

帝国的形成：国家是ICA的基本个体，可表示为一个N维向量，其每个元素为待优化的状态量.先随机产生Npop个国家，按势力大小(代价函数值)选取势力较大的前Nimp个国家作为帝国主义国家，剩下的则都为殖民地，并为每个帝国主义国家分配殖民地，形成初始的Nimp个帝国.

同化和革命：ICA以殖民地向其所属帝国主义国家移动来模拟同化过程.同时，在殖民地内部其坐标位置也会随机发生改变，即革命过程.当一个殖民地国家到达新的位置后，若其势力超过所属帝国主义国家，则交换两者位置，该殖民地成为新的帝国主义国家，而原来的帝国主义国家沦为殖民地.

竞争机制：帝国之间通过竞争实现扩张，势力越大的帝国(总代价函数值越小)越有可能控制并占有势力较弱帝国的殖民地.

帝国的灭亡：在竞争机制作用下，势力弱小的帝国不断丢失殖民地，当一个帝国失去所有殖民地时，帝国灭亡.ICA终止时只剩一个帝国并处在同一个位置，即最优解.

3.2 ICA的改进

在原始ICA中，帝国之间通过竞争实现彼此的信息交互.然而每次迭代，帝国竞争只是把最弱的殖民地并入最强帝国，对帝国势力大小影响很小.为了加强帝国之间的信息交互，提高ICA的收敛速度和运算效率，文中引入克隆进化[18]的思想，具体方法如下.

1)将帝国主义国家按势力从大到小排序，并依次进行克隆，克隆个数为

(15)

2)对第i个帝国的克隆群体Ci进行变异，产生新的变异群体Hi：

Hi=Ci+φiUNCi×nImax

(16)

(17)

式中:m为帝国个数；n为问题维度；φ为变异概率，帝国势力越小，变异概率越大;UNCi×n表示一个NCi×n阶矩阵，其元素服从[0,1]区间上的均匀分布；Imax为势力最大的帝国主义国家.

3)将变异群体Hi随机划分为4个一组，每组按式(16)进行交叉计算：

Ki=Hi,1-Hi,2+Hi,3-Hi,4

(18)

4)取Ki和Hi中势力最大的k个克隆变异个体取代当前势力最弱的k个帝国主义国家.

上述克隆进化算子虽然显著加快了帝国竞争与合并的速度，却也增加了ICA陷入局部最优的风险.因此，在每次迭代中使帝国以概率pm进行合并，适当减小pm能够解决算法易早熟收敛的问题，进一步提升ICA的整体性能.

4 算法流程

用上述ICA求解PLF问题的具体步骤如下：

步骤1 确定所有输入随机变量(负荷、风速、太阳辐射强度等)的PDF；

步骤2 给定样本数量N；

步骤3 由PDF得到输入随机变量的样；

步骤4 在约束范围内随机选取未知量(电压幅值、相角)的值，得到输入向量x；

步骤5 由式(11)-(14)计算目标函数Z的值；

步骤6 重复执行ICA直到达到终止条件或迭代次数n；

步骤7 求得所有输出变量(电压幅值、相角、支路功率、损耗等)的值；

步骤8 抽取新的输入样本；

步骤9 重复步骤4-8，直到第N个输入样本计算结束；

步骤10 统计求得各输出变量的PDF和CDF.

图1示出了基于改进ICA的PLF算法流程，其中N为样本数，迭代次数定为n.

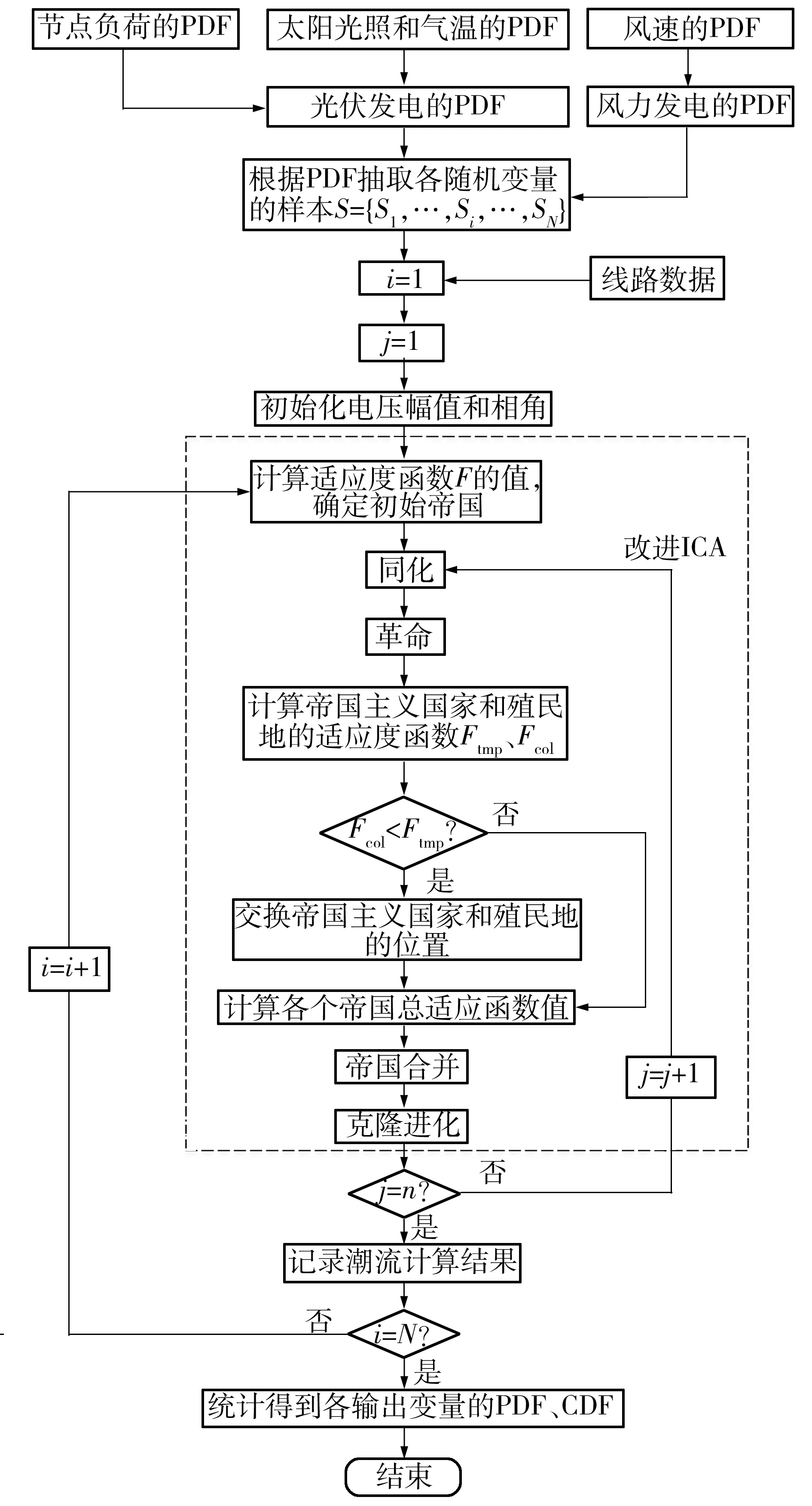
图1 基于改进ICA的随机潮流算法流程

5 算例分析

为了评估所提算法的性能，以IEEE-33配电系统为例进行仿真计算.在系统中加入4个DG(2台额定功率为150 kW的风机，2个额定功率为100 kW的太阳能电池板)和5条馈线(虚线所示)形成微网，图2给出了修改后IEEE-33节点系统的拓扑结构(由纯辐射型变为弱环型).其中，添加的5条馈线参数均为R=0.5Ω,X=0.5Ω，风机(WT)和PV模块的具体参数见表1.

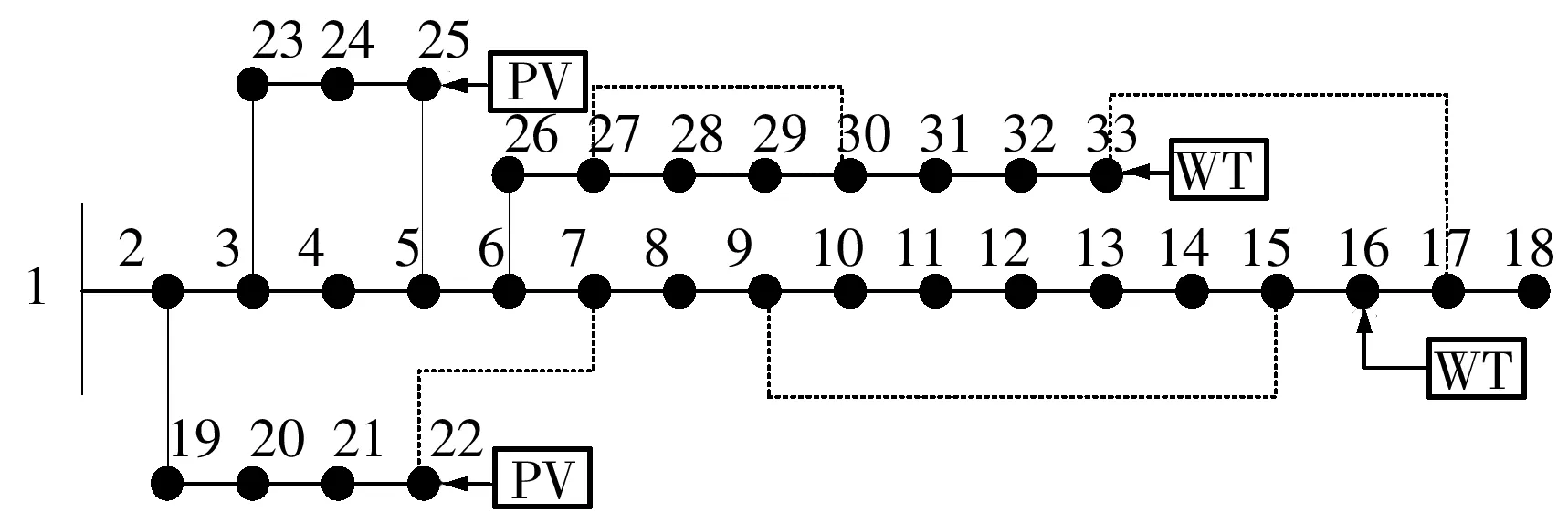
图2 修改后的IEEE-33节点测试系统

模块参数WTvin=3m/s,vR=13m/s,vout=25m/s,PR=150kW,k=8PVPSTC=100kW,k=0.001,Tr=25℃

用所提算法分别计算有DG和无DG两种场景下系统各节点的电压幅值，并与蒙特卡洛仿真所得结果进行比较.表2列出了改进ICA的相关参数，MCS取样本数N=5 000.由第1节的随机模型获得WT和PV的输出功率样本分布如图3所示.

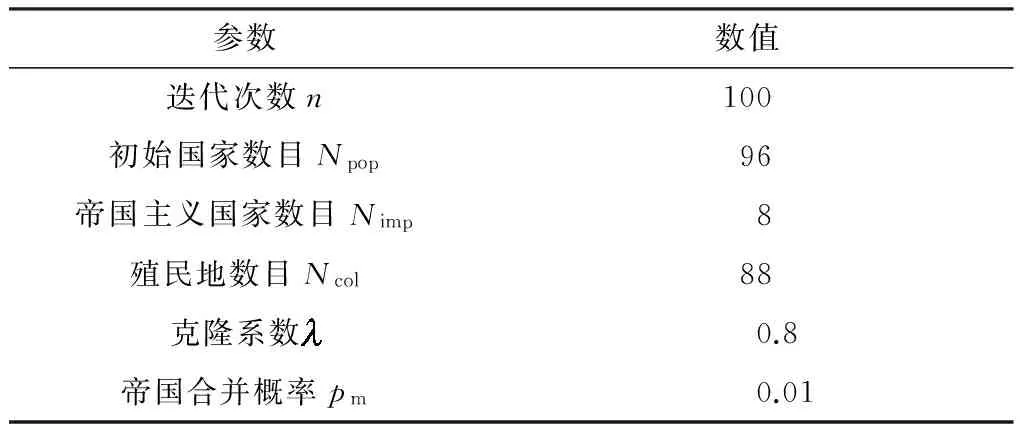
表2 改进ICA的参数设置

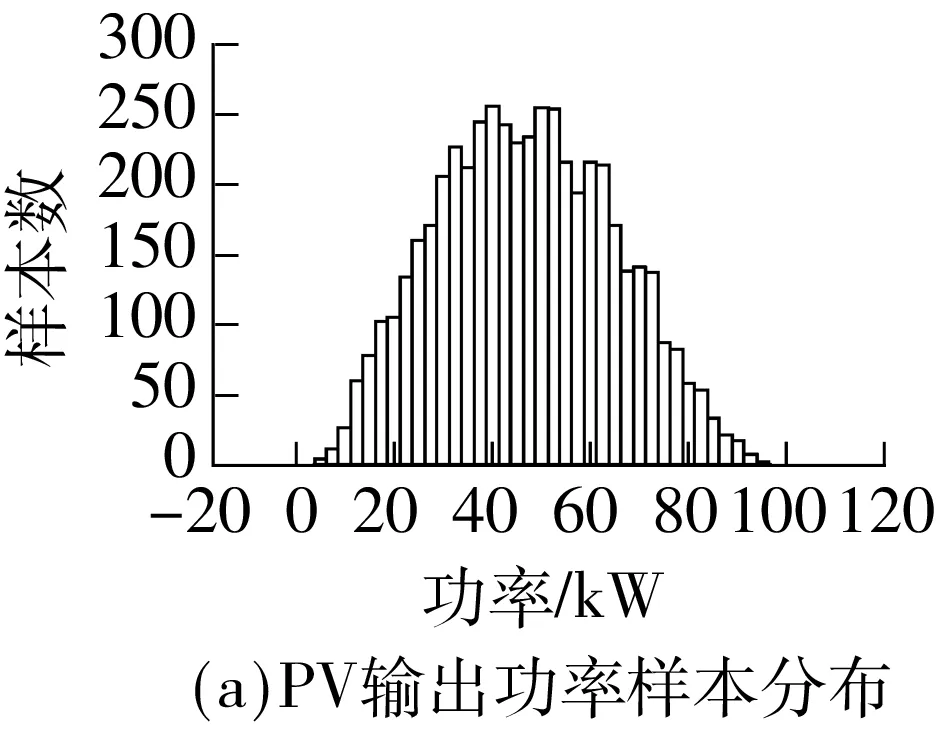
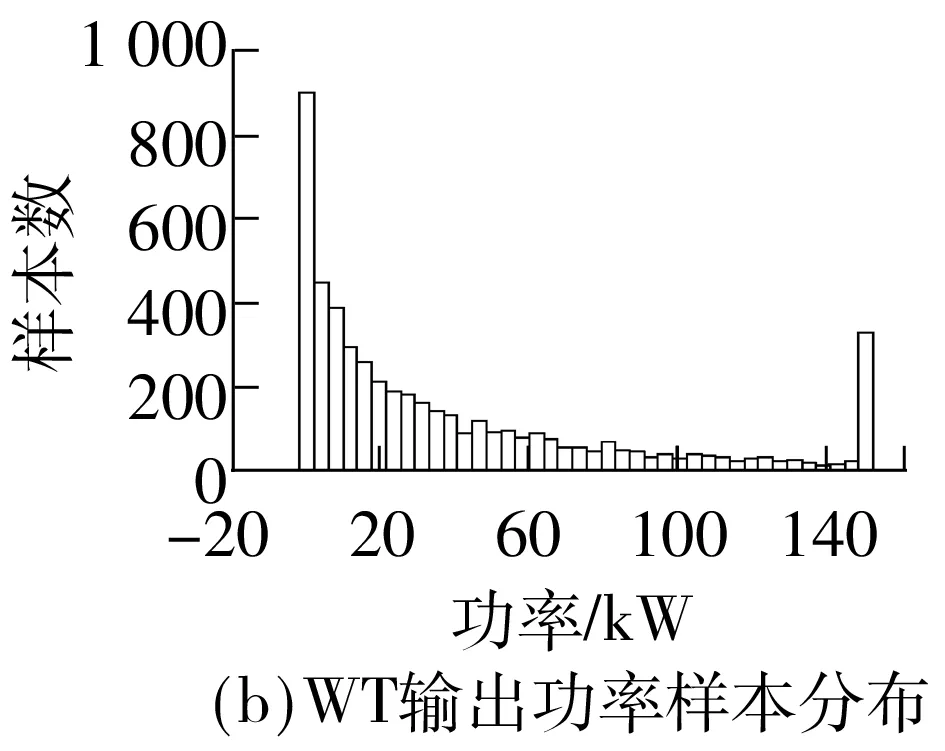
图3 DG输出功率的样本分布

表3和图4分别给出了各节点电压的计算结果及分布情况，以节点23为例，其在接入DG前后电压的CDF如图5所示.

综合以上图表可知，加入DG能够相应提升系统各节点的电压水平，距离接入点越近，DG容量越大，则节点电压上升越明显，且所提算法与MCS所得结果(均值、均方差和概率分布)基本一致，具有较高的计算精度.为了综合、全面地衡量所提算法的有效性，需要量化计算误差，引入输出变量期望值与标准差的相对误差指标[21]：

(19)

(20)

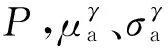
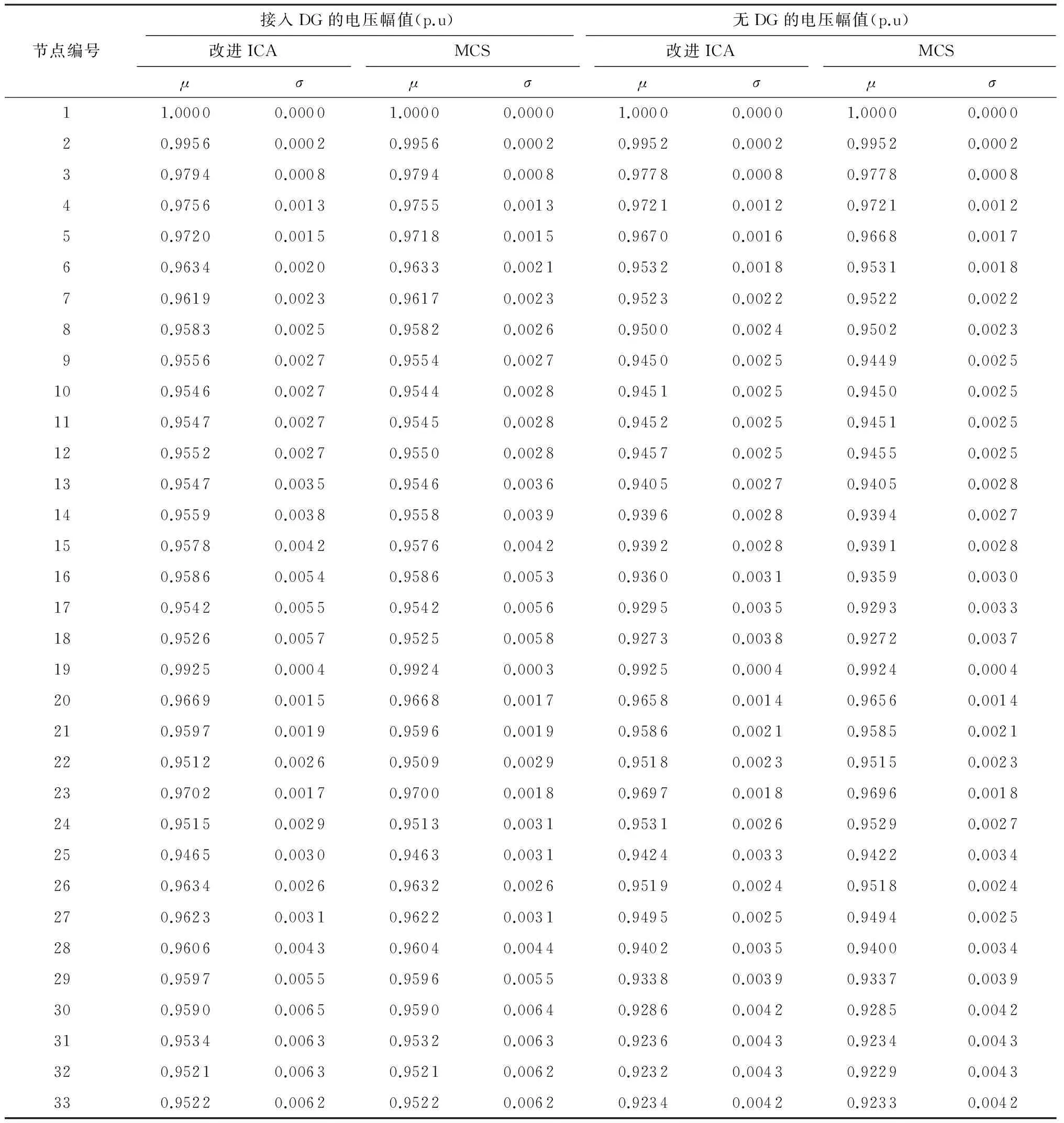
表3 两种场景下各节点电压的计算结果

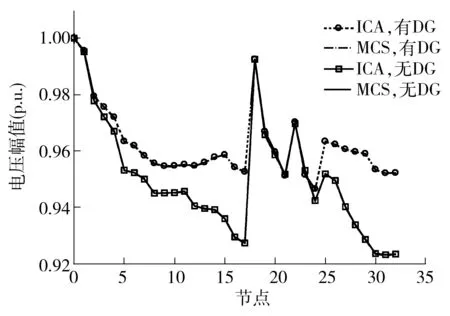
图4 系统各节点的平均电压分布

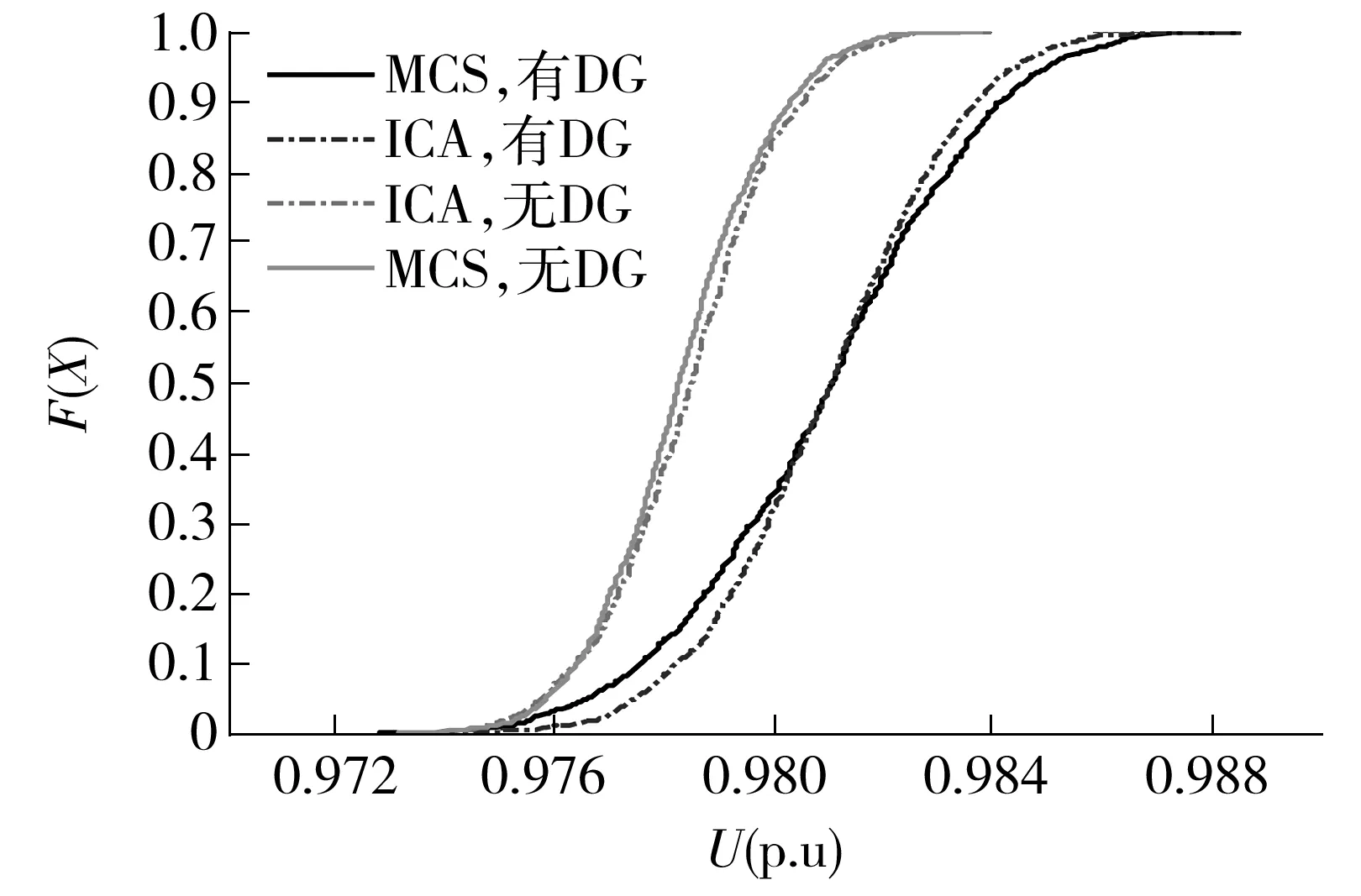
图5 两种场景下节点23电压的CDF

Fig.5 CDF of voltage magnitude at bus 23 considering two scenarios

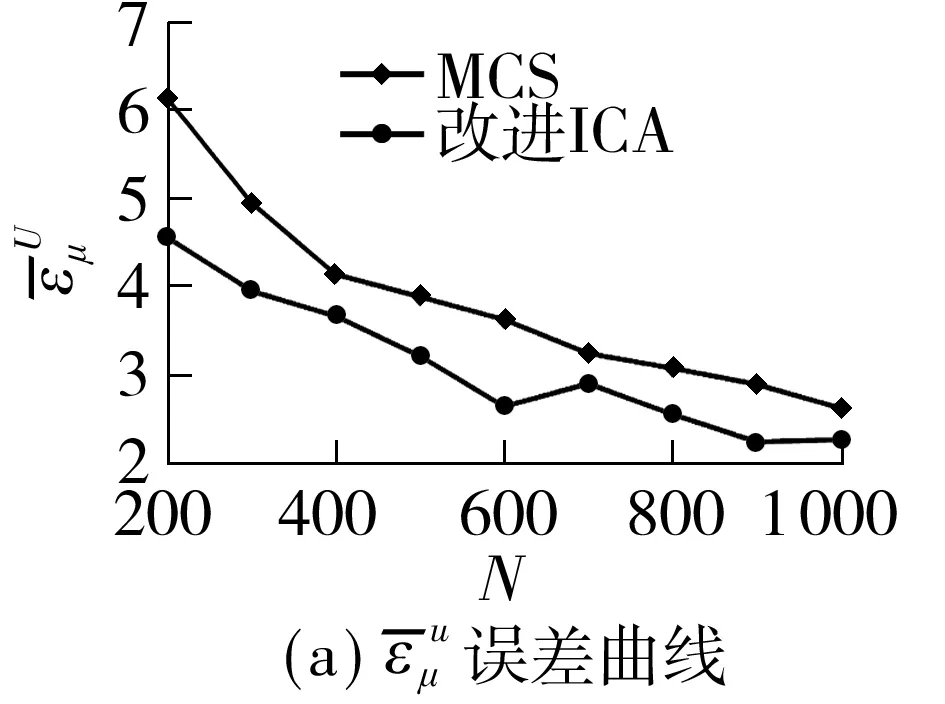
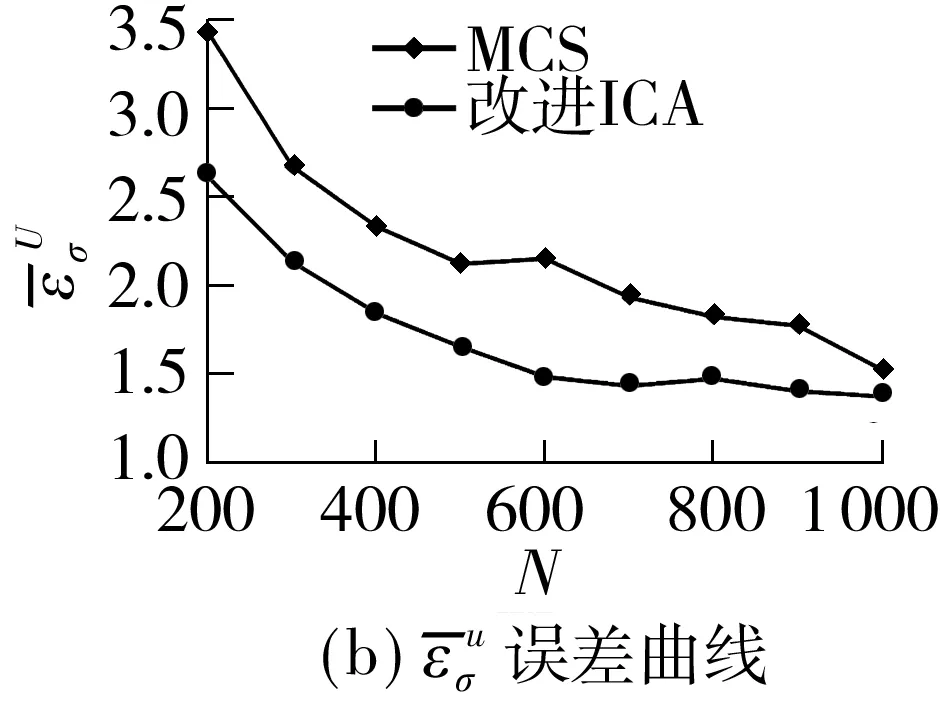
图6 所提方法与MCS的误差特性比较

Fig.6 Error curves comparisons of MCS and proposed method

对弱环结构的配电网来说，由于线路参数R/X的值较大，用N-R法在每次潮流计算时可能会出现病态情况[22].表4测试了不同阻抗比网络(原算例电抗不变，电阻乘以阻抗系数K)所提算法和N-R法相应的迭代收敛情况.其中K>2时，N-R法不收敛，而所提算法的收敛性并无显著变化.令终止条件ε=10-9，用所提算法与其他智能算法(原始ICA、GA、PSO)各重复100次仿真计算，比较它们的平均迭代次数(如表5所示)，其中文中算法仅需迭代12次就能够达到目标精度，远小于其他算法.可见文中对ICA的改进能够显著加快收敛速度.

表4 不同阻抗系数下的潮流计算比较

Table 4 Comparisons of load flow at different impedance coefficients

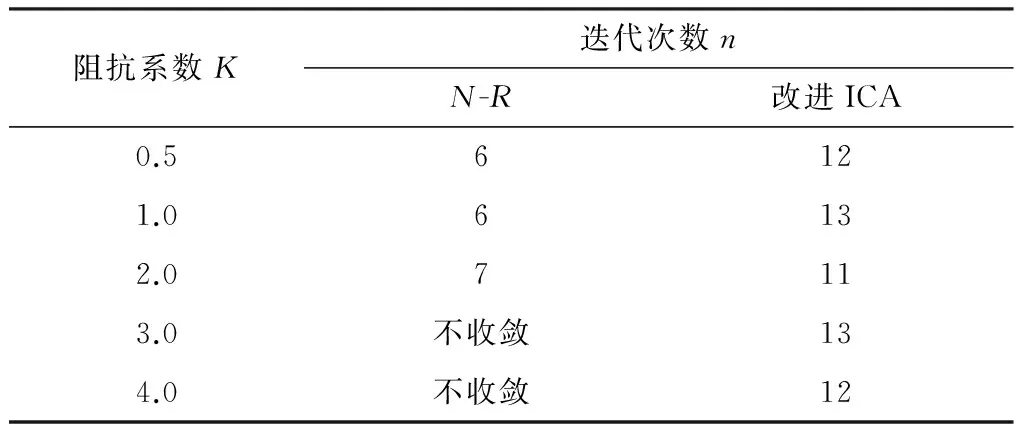
阻抗系数K迭代次数nN-R改进ICA0.56121.06132.07113.0不收敛134.0不收敛12

表5 不同算法的迭代次数比较

6 结语

针对未来智能配电网中大量DG的接入所带来的不确定因素增多、网络拓扑结构改变等问题，文中提出了一种启发式随机潮流算法.该算法在原始ICA的基础上引入克隆进化的思想，加强了帝国间的信息交互，能够适应不同DG渗透率下纯辐射型、弱环型和纯环状的配电网络，并具有良好的收敛性.但由于启发式算法普遍计算量大，且每个采样点都要一一计算，整个过程耗时较长.后续将研究通过提高采样效率、优化ICA的参数设置及分布式并行计算等手段，进一步加快算法的计算速度，提升其有效性和实用性.

[1] ZHU Y,TOMSOVIC K.Adaptive power flow method for distribution systems with dispersed generation [J].IEEE Transactions on Power Delivery,2002,17(3):822-827.

[2] BORKOWSKA B.Probabilistic load flow [J].IEEE Transactions on Power Apparatus and Systems,1974,93(3):752-759.

[3] 朱星阳,刘文霞,张建华,等.电力系统随机潮流及其安全评估应用研究综述 [J].电工技术学报,2013,28(10):257-270. ZHU Xing-yang,LIU Wen-xia,ZHANG Jian-hua,et al.Reviews on power system stochastic load flow and its applications in safety evaluation. [J].Transactions of China Electrotechnical Society,2013,28(10):257-270.

[4] 梁惠施,程林,刘思革.基于蒙特卡罗模拟的含微网配电网可靠性评估 [J].电网技术,2011,35(10):76-81. LIANG Hui-shi,CHENG Lin,LIU Si-ge.Monte Carlo simu-lation based reliability evaluation of distribution system containing microgrids [J].Power System Technology,2011,35(10):76-81.

[5] 丁明,李生虎,洪梅.电力系统概率分析中的K均值聚类负荷模型 [J].电力系统自动化,1999,23(19):51-54. DING Ming,LI Sheng-hu,HONG Mei.TheK-means cluster based load model for power system probabilistic analysis [J].Automation of Electric Power Systems,1999,23(19):51-54.

[6] CHEN Y,WEN J,CHENG S.Probabilistic load flow method based on Nataf transformation and Latin hypercube sampling [J].IEEE Transactions on Sustainable Energy,2013,4(2):294-301.

[7] SU C L.Probabilistic load-flow computation using point estimate method [J].IEEE Transactions on Power Systems,2005,20(4):1843-1851.

[8] 杨欢,邹斌.含相关性随机变量的概率潮流三点估计法 [J].电力系统自动化,2012,36(15):51-56. YANG Huan,ZOU Bin.Three point estimate method for probabilistic load flow with correlated variables [J].Automation of Electric Power Systems,2012,36(15):51-56.

[9] AIEN M,FOTUHI-FIRUZABAD M,RASHIDINEJAD M.Probabilistic optimal power flow in correlated hybrid wind-photovoltaic power systems [J].IEEE Transactions on Smart Grid,2014,5(1):130-138.

[10] YUAN Y,ZHOU J,JU P,et al.Probabilistic load flow computation of a power system containing wind farms using the method of combined cumulants and Gram-Charlier expansion [J].IET Renewable Power Generation,2011,5(6):448-454.

[11] 胡泽春,王锡凡,张显,等.考虑线路故障的随机潮流 [J].中国电机工程学报,2005,25(24):26-33. HU Ze-chun,WANG Xi-fan,ZHANG Xian,et al.Probabilistic load flow method considering branch outages [J].Proceedings of the CSEE,2005,25(24):26-33.

[12] VON Mises R.Mathematical theory of probability and statistics [M].New York:Academic Press,2014.

[13] HONG Y Y,LIN F J,LIN Y C,et al.Chaotic PSO-based varcontrol considering renewables using fast probabilistic power flow [J].IEEE Transactions on Power Delivery,2014,29(4):1666-1674.

[14] GOMEZ-GONZALEZ M,RUIZ-RODRIGUEZ F J,JURADO F.A binary SFLA for probabilistic three-phase load flow in unbalanced distribution systems with technical constraints [J].International Journal of Electrical Power & Energy Systems,2013,48:48-57.

[15] 程卫东.含风电场电力系统的概率潮流 [D].北京:华北电力大学,2010.

[16] 董雷,程卫东,杨以涵.含风电场的的电力系统概率潮流计算 [J].电网技术,2009,33(16):87-91. DONG Lei,CHENG Wei-dong,YAN Yi-han.Probabilistic load flow calculation for power grid containing wind farms [J].Power System Technology,2009,33(16):87-91.

[17] ATASHPAZ-GARGARI E,LUCAS C.Imperialist competi-tive algorithm:an algorithm for optimization inspired by imperialistic competition [C]∥IEEE Congress on Evolutionary Computation.[S.l.]:IEEE,2007:4661-4667.

[18] GONG M,JIAO L,DU H,et al.Multiobjective immune algorithm with nondominated neighbor-based selection [J].Evolutionary Computation,2008,16(2):225-255.

[19] GLOVER J D,SARMA M,OVERBYE T.Power system analysis &design,SIversion [M].Boston:Cengage Learning,2011.

[20] 陈雁.含大规模风电场电力系统的运行与规划方法研究 [D].湖北:华中科技大学,2012.

[21] ZHANG P,LEE S.T.Probabilistic load flow computation using the method of combined cumulants and Gram-Charlier expansion [J].IEEE Transactions on Power System,2004,19(1):676-682.

[22] TENG J H.A direct approach for distribution system load flow solutions [J].IEEE Transactions on Power Delivery,2003,18(3):882-887.

Improved Probabilistic Load Flow Calculation of Distribution Grids with Distributed Generation

HUANGYu1XUQing-shan1LIUJian-kun2WEIPeng2

(1.School of Electrical Engineering, Southeast University, Nanjing 210096, Jiangsu, China;2.Jiangsu Electric Power Research Institute, Nanjing 210003, Jiangsu, China)

With the continuous increase of the proportion of distributed generations (DG) in distribution grids, power systems face more and more challenges, such as the increase of uncertainty and the change of grid structure. The conventional load flow calculation method is unable to deal with such a great number of uncertainties in grids. In order to solve this problem, a probabilistic load flow calculation method based on the imperialist competitive algorithm (ICA) is proposed, which can easily take into account all kinds of topology structures, different DG penetration levels and multiple constraint conditions of complicated networks, with good convergence as well. Moreover, for the purpose of improving the searching ability and convergence rate of the algorithm, a clone evolution operator is introduced in ICA. The modified IEEE-33 distribution system is used for simulation and the results are compared with those obtained via Monte Carlo simulation (MCS). It is found that the proposed method is of high precision and great practical value.

probabilistic load flow; smart distribution grid; distributed generation; imperialist competitive algorithm; clone evolution

2015-12-24

国家自然科学基金资助项目(51377021)；东南大学中央高校基本科研业务费专项资金资助项目(2242016K41064)；国网公司科技项目 Foundation item: Supported by the National Natural Science Foundation of China(51377021)

黄煜(1992-)，男，博士生，主要从事新能源发电技术、微电网运行与控制等的研究.E-mail:hy_1992@foxmail.com

1000-565X(2017)04-0044-07

TM 74

10.3969/j.issn.1000-565X.2017.04.007