配电网分布式风电与电池储能的协调优化配置*

欧阳森 陈欣晖 杨家豪

(华南理工大学 电力学院∥广东省绿色能源技术重点实验室， 广东 广州 510640)

配电网分布式风电与电池储能的协调优化配置*

欧阳森 陈欣晖 杨家豪

(华南理工大学 电力学院∥广东省绿色能源技术重点实验室， 广东 广州 510640)

分布式风电(DWG)与电池储能(BES)在配电网中的位置与容量均会影响配电网的运行状态，为提高风电消纳能力，削弱风电出力不确定性对配电网运行的影响，在规划阶段应对二者进行选址定容协调优化配置.文中以计及风-储系统的随机潮流全面反映含DWG及BES的配电网运行状态及不确定性，以等年值综合收益最大化作为目标函数建立机会约束规划模型；提出改进多种群遗传算法，引入有效的寻优机制以增强算法性能.IEEE 33节点配电网算例的仿真分析验证了优化模型的合理性及算法的有效性.

配电网；分布式风电；电池储能；选址定容；协调优化；随机潮流

在节能减排的背景下，电商往往在配电网中接入分布式风电(DWG)就近向用户侧提供电能.但受自然条件的影响，DWG出力具有随机波动的特征，不利于配电网稳定运行.随着储能技术的发展，将电池储能(BES)应用于配电网中与DWG联合运行，可成为提高配电网风电消纳能力以及平抑风电波动的有效手段[1-2].

DWG及BES选址定容的合理性将影响其并网后系统的运行状态与综合效益.国内外学者对此开展了大量研究，文献[3]中应用机会约束规划建立DWG的选址定容优化配置模型，文献[4-5]中进一步考虑主动管理模式、电力市场环境等对DWG规划的影响.现阶段BES容量优化配置模式多面向已接入分布式电源的配电网[6-9].考虑到储能的充放电策略对优化配置结果的影响，文献[10]中在对微电网综合负荷进行削峰填谷的控制背景下，提出基于上下限约束法的混合储能容量优化配置方法；文献[11]中探讨了在电力市场环境下，以配电公司的净收益最大为目标建立考虑运行策略及投资主体利益的电池储能系统优化配置模型.

然而，DWG与BES的运行存在强耦合，不适宜各自孤立地进行分散优化配置.在新配电网规划阶段，同时进行二者捆绑式的选址定容协调优化将更有利于提升配电网的风电消纳能力，改善系统运行状态.目前考虑DWG与BES选址定容协调优化的研究仍较少，文献[12]中考虑分布式电源及储能的随机特性对其运行状态进行划分，根据状态组合转化为确定性问题进行配电网的扩展规划，文献[13]中考虑分布式电源与充电站的协调规划，结果表明协调规划可获得更合理的规划方案.对DWG与BES进行选址定容协调优化，可于规划阶段就考虑DWG与BES联合运行下可能的系统状态，兼顾设备的有效利用，减少不必要的投资.

文中将利用计及风-储联合系统概率模型的随机潮流[14]获取配电网状态变量的概率分布，描述系统的运行状态，在此基础上考虑DWG与BES捆绑的选址定容协调优化，以等年值综合收益最大化为目标函数，建立DWG与BES联合系统的机会约束规划模型；同时，提出二者选址定容协调优化的寻优机制并引入到所提出的改进多种群遗传算法(IMPGA)中，增强算法的寻优性能，最终对文中方法的有效性及算法的优化性能进行验证分析.

1 DWG与BES选址定容协调优化模型

从经济性角度而言，增大DWG并网容量可更充分地利用风能，增加发电收益；而BES仅作为存储环节且存在充放电效率和成本问题，应在满足调控需求的情况下尽可能降低其配置容量.另外从系统安全运行的角度考虑，DWG并网容易导致系统运行状态(如关口有功功率)波动以及节点电压的越限概率增大，不利于系统的安全运行，而足够容量的BES将有效减弱系统运行不确定性，提高风电消纳能力并优化系统运行.针对以上问题，文中建立的DWG与BES选址定容协调优化模型在保证系统运行状态安全的情况下，追求经济性最优.模型对部分状态变量约束采取机会约束.

1.1 计及风-储联合系统的随机潮流

随机潮流是分析分布式电源并网后系统运行状态不确定性的有效工具，其计算结果是在输入随机扰动时系统稳态解的宏观统计[15].

文献[14]中提出计及风-储联合系统的随机潮流计算模型，该模型在DWG并网点配置BES，考虑BES的运行特性与充放电策略，对DWG并网点功率注入概率模型进行修正.为了最大限度利用可再生能源及简化控制策略，DWG采用单位功率因数运行，DWG并网点和负荷节点视为有功无功(PQ)节点.

模型修正的示意图如图1所示，通过实际数据统计获取日内DWG出力的统计特性模型，柱体的宽度代表出力区间，柱体高度表征一天内DWG在此出力区间内的时间长短.运用场景分析法可把每个出力区间划分为一个场景，区间中值为该场景出力值.纵坐标可通过时间尺度换算转换为概率.

图1 模型修正示意图

由图1可看出，BES的充放电行为可以在模型中以平移操作的形式来近似描述，DWG出力过大时BES充电，DWG出力过小时BES放电，使得平抑后DWG并网点的出力波动范围缩小.

通过给定具体时间窗口可以根据BES的参数对概率模型进行修正，从而近似描述配置BES后风储整体出力的概率统计情况.具体修正机理与修正流程见文献[14].

文中基于文献[14]方法，采取基于半不变量及Gram-Charlier级数的随机潮流计算模型，简化优化过程中对风-储联合运行的描述，即利用随机潮流结果来分析不同配置方案下配电网的运行状态，计算DWG与BES并网后系统状态变量的概率分布，从而判断模型中机会约束的满足情况.

1.2 目标函数

考虑DWG和BES设备的运行年限，将总投资换算为等年值投资，以等年值综合收益最大化作为优化目标，目标函数为

maxF=Csale+Cemis-Closs-Cinv-Cser

(1)

式中，Csale为风电售电收益,Cemis为废气减排收益,Closs为系统网损费用,Cinv为等年值设备投资费用,Cser为设备运行维护费用.各项分量计算方法如下.

(1)风电售电收益

DWG靠近用户侧直接接入配电网，可以利用风能发电，向用户就近提供电能，带来售电收益.

售电收益为

(2)

式中，Pexp_ j为第j个DWG并网点的有功出力期望值,tuse_ j为第j个DWG并网点风机的年运行小时数,fon为风电上网电价.

(2)废气减排收益

风能发电可以减少配电网从上层电网索取的有功功率，从而减少部分主网火力发电量，间接实现废气减排，这部分收益为

(3)

式中，kt为火力发电比例系数，femis为单位电量排放费用.

(3)系统网损费用

DWG的合理接入为周边负荷提供有功功率，避免了部分有功功率的远距离传输，从而降低系统网损.系统网损费用的计算式为

Closs=PlossTusefsys

(4)

式中，Ploss为随机潮流计算获得的网损期望值,Tuse为系统的等效年利用小时数,fsys为系统侧电价.

(4)等年值设备投资费用

文中将设备总投资换算为等年值投资以进行年综合效益的测算，年现值系数α可表示成以折现率和设备使用年限表示的表达式，即

(5)

式中，r为折现率，L为设备使用年限.则DWG及BES的等年值投资费用分别为

(6)

式中：fDWG及fBES分别为DWG及BES的单位投资费用；PDWG_ j及CBES_ j分别为第j个DWG并网点安装的DWG额定容量及BES配置容量；fsDWG_ j及fsESS_ j分别为单个DWG及ESS并网点的建设投资，当该点未配置DWG或ESS时，则相应项取0；LDWG及LBES分别为DWG及BES的设备使用年限.

则等年值设备投资费用为

Cinv=ADWG+ABES

(7)

(5)设备运行维护费用

为简化处理，DWG及BES整体的年运行维护费用根据DWG发电量期望值进行测算：

(8)

式中，fser为综合单位电量运行维护费用.

1.3 约束条件

等式约束为潮流方程约束，而不等式约束从系统安全运行和风电充分消纳的角度进行设计.

(1)关口功率约束

考虑DWG群接入对配电网与上层电网有功交换量的影响，对关口有功功率采取概率约束，即关口有功功率在配电网调度层所设置的有功交换上、下限之间的概率应满足置信要求.其次，关口有功功率波动率也应低于限值.

(9)

(2)节点电压约束

对节点电压同样采取机会约束，即各节点电压在电压考核上、下限之间的概率应满足置信要求，同时系统电压波动范围应低于限值.

(10)

(3)DWG及BES配置容量约束

文中通过合理规划BES能够提高风电的消纳能力，且上文的关口功率约束能够保证在高置信水平下系统功率不倒送，因此这里不对DWG渗透率进行约束，仅要求各待选配置节点的DWG与BES配置容量不超过限值.

(11)

式中，PDWG_ j_max为节点j允许接入的DWG额定功率最大值，σmax为BES容量约束系数.

2 优化模型的求解

文中优化模型中各配置点的DWG额定功率、BES配置容量以整数模块化编码方式来表示，该优化问题为一个混合非线性整数规划问题.

但该模型的求解具有以下难点：

1)随机潮流中涉及BES对DWG并网点功率注入概率模型的修正，在优化模型中此操作无法简单以解析形式表示，因而难以使用基于导数信息的优化算法；

2)优化模型中包含较多约束条件，包括状态变量的机会约束，仅依靠智能算法随机寻优，在没有一定引导机制下将容易产生大量不可行解；

3)DWG的并网容量应尽量大，而BES的容量尽量小，才可保证经济性，而经济性最优时往往系统运行的安全性约束无法完全满足.本问题的趋优解集与不可行解的过渡带较小，若搜索到不可行解而直接舍弃会降低寻优的效率.

2.1 MPGA算法基本原理

相比于遗传算法(GA)，多种群遗传算法(MPGA)有效解决了算法的控制参数选择对结果的影响，突破了标准GA依靠单一种群进行进化寻优的框架，引入多个种群同时进行优化搜索，不同种群赋予不同的交叉概率与变异概率通过移民操作来增强寻优性能，其最优解的获取是多种群协同进化的综合结果[16].

算法的结构示意图如图2所示.

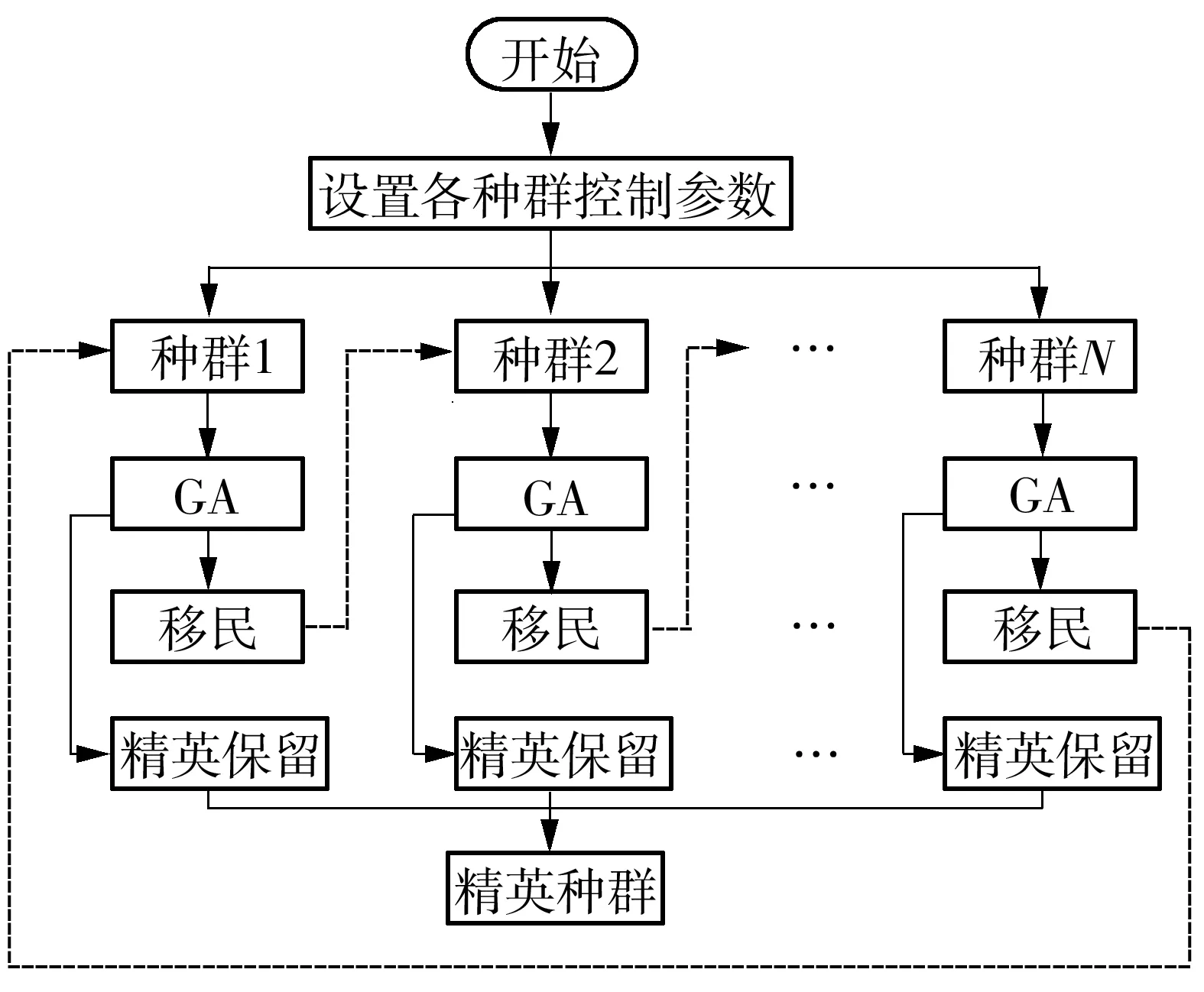
图2 MPGA流程结构图

2.2 寻优机制的引入

根据随机潮流计算结果可以明确以下几点DWG与BES并网后对系统运行状态的影响规律：

1)DWG的并网容量增加将引起关口有功功率波动范围增大，而BES刚好相反；

2)随着支路中DWG接入总容量增加，该支路的电压波动范围增大，而同理合理配置BES可以有效减小电压波动范围；

3)非本支路接入的DWG与BES的容量大小对本支路电压波动范围的影响较弱；

4)考虑到对仅含PQ节点的辐射形配电网进行随机潮流计算，若随机变量相互独立，线路末端的功率注入不确定性越强则系统整体的状态变量不确定性也越强.

文中基于上述规律提出一种协调优化寻优机制，以求增强智能算法的寻优性能，其核心思想是在优化过程中对个体的进化方向进行选择.

针对前面阐述的模型求解难点2)和3)，文中算法寻优机制将不在迭代过程中完全舍弃不可行解，而是促使每代的可行解与不可行解均向趋优解集进化.从解的可行性分为以下两方面操作：

1)对于可行解，即满足系统安全运行约束，为提高目标函数值应继续适当增加DWG并网容量、减少BES并网容量以提高经济性；

2)对于不可行解，即系统安全运行约束已得不到满足，应牺牲一定的经济性减少DWG容量或增加BES的配置容量.

通过以上操作能够以较大概率指定个体进化的大致方向，增强潜在最优解所存在的边界范围附近的算法寻优能力.

2.3 MPGA算法的改进

文中提出一种IMPGA，引入上文所提出的寻优机制的思想，设计相应的进化操作.

(1)编码方式与个体的产生

采取整数编码，假设配电网内有m个待选的可安装DWG的节点，则每个个体的基因长度为2m.此外每一个体还对应一组性状位，表征各支路电压与关口功率违背约束的情况，作为后续进化操作的判断标准.

初始种群的产生首先在各节点准入的DWG容量范围内产生各节点的DWG并网机组数，其次在含有DWG机组的节点对应的BES基因位在容量约束范围内随机产生BES容量.

(2)选择操作与移民操作

选择操作采取轮盘赌博法，并采取精英保留策略以保存每代的优势个体不被破坏.每隔一定代数利用移民操作交换各种群间的优势个体.

(3)交叉操作

在满足交叉概率的情况下随机选择两个个体，并随机选择单个或多个表征DWG接入容量的基因位进行交叉，相应的BES位同步进行交叉操作.

(4)重组操作

基于2.2节中的规律特性，可以明确个体编码中表示各支路DWG与BES并网容量的序列排序也会对解的优劣产生影响.基因重组操作即对个体的编码序列重置，使其向DWG与BES的趋优分布改变，设计如下两种操作策略.

策略1 在满足重组概率的情况下对各支路DWG并网容量排序，使上游节点到下游节点的DWG并网容量依次减少，各节点对应的BES配置容量按同样顺序重置.

策略2 与策略1排序相反.

(5)变异操作

同样设计两种操作策略，且对可行解与不可行解进行区别操作.

对于可行解，在满足变异概率情况下随机选取其中一个已有DWG接入(该位编码非零)的节点，策略1为在较大概率下向DWG容量增加的方向变异，策略2为使其对应的BES基因位在较大概率下向BES容量减小的方向变异.

对于不可行解，根据性状位进行判断：

1)若某支路电压波动范围越限，策略1强制使某一表征该支路DWG接入容量的基因位向DWG容量减少的方向变异，策略2强制使某一表征该支路BES接入容量的基因位向BES容量增加的方向变异；

2)若关口功率波动越限，策略1随机使某一表征系统DWG接入容量的基因位向DWG容量减少的方向变异，策略2随机使某一表征系统BES接入容量的基因位向BES容量增加的方向变异.

3 算例分析

3.1 测试系统与优化参数

文中以IEEE33节点配电网作为测试系统，其中DWG接入的待选节点为12、16、21、28、32，系统接线图见图3.DWG单机额定功率为100 kW，节点最大安装机组数为10台，该地区DWG的近似出力特性见图4.BES的单体容量为100 kWh，充放电效率均满足η=0.85，最大充放电功率Pmax与CBES成正比.

各节点负荷概率模型取正态分布，期望值取IEEE33节点测试系统的负荷数据[14]，描述各节点负荷波动的标准差取σP=σQ=0.12，首端电压取1.025.

优化模型参数如表1所示.

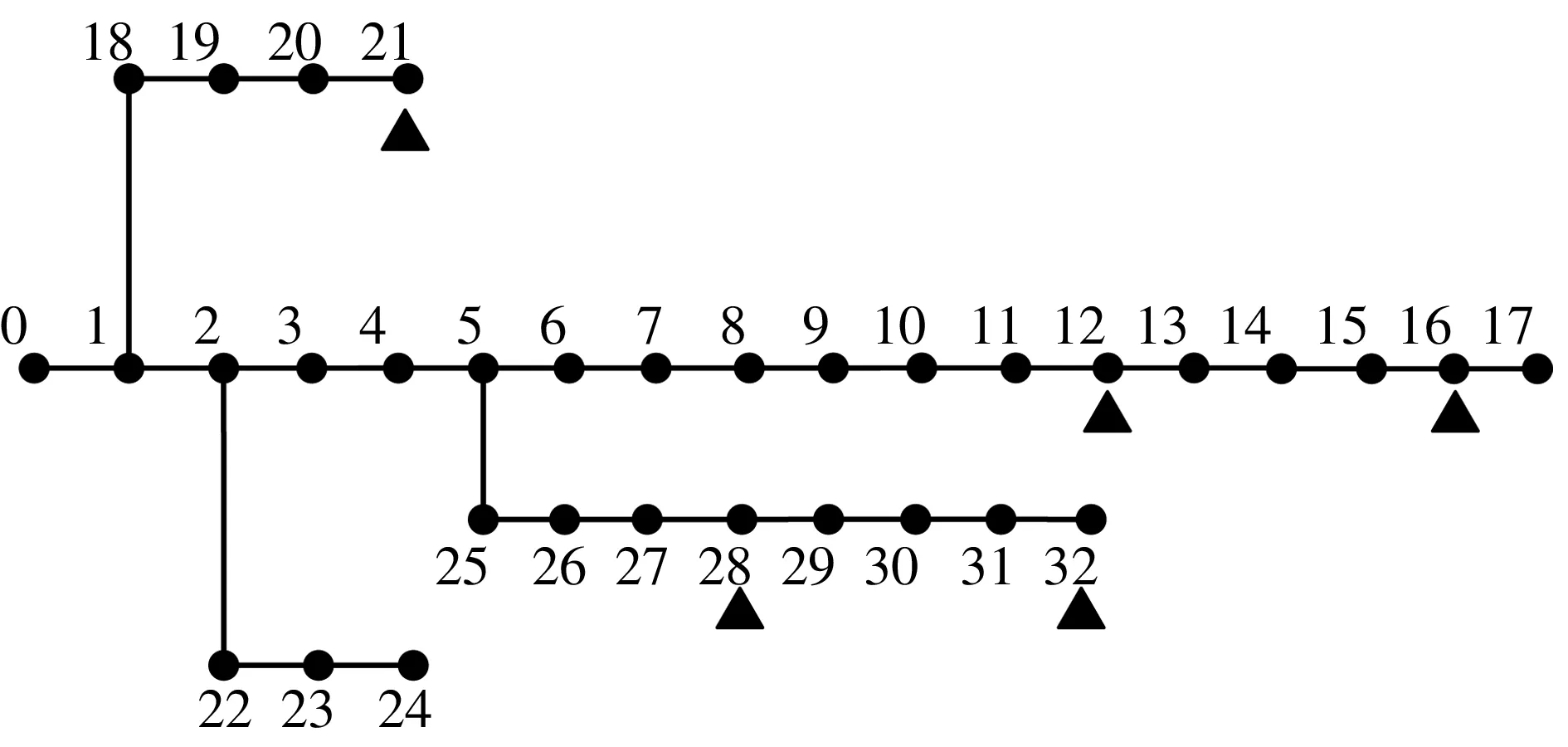
图3 IEEE33节点配电网

图4 DWG出力模型

参数类别参数名称参数值目标函数参数风机年运行小时数tuse/h5000系统年利用小时数Tuse/h8760风电上网电价fon/(元(kW·h)-1)0.5系统侧电价fsys/(元(kW·h)-1)0.4单位电量排放费用femis/(元(kW·h)-1)0.2DWG单位投资费用fDWG/(元(kW·h)-1)7000单个DWG并网点建设投资fsDWG_j/万元80BES单位投资费用fBES/(元(kW·h)-1)8000单个BES并网点建设投资fsESS_j/万元60单位电量运行维护费用fser/(元(kW·h)-1)0.15火力发电比例系数kt/%65折现率r/%8DWG设备使用年限LDWG/年20BES设备使用年限LBES/年20BES容量约束系数σmax/%100约束条件参数置信度E/%99关口有功上限PGmax/kW3000关口有功下限PGmin/kW0关口波动限值1/%50电压考核上限Vmax(p.u.)1.05电压考核下限Vmin(p.u.)0.95电压波动限值2(p.u.)0.05

对于IMPGA的算法参数设置如下：种群数目取4，种群规模取30，最大进化代数取100，交叉概率取0.75，重组概率取0.25，变异概率取0.15.4个种群分别使用重组策略1、2与变异策略1、2的组合.

3.2 方案对比分析

采取4种方案对测试系统进行DWG与BES的选址定容协调优化，并对各方案进行对比分析.

方案1 在满足系统运行约束的条件下，不考虑配置BES，仅作DWG的选址定容优化；

方案2 以目前DG规划中允许的最大渗透率(50%)分散接入DWG后，再作BES的分散选址定容以保证系统满足安全运行的约束条件；

方案3 同方案2，但DWG采取集中接入模式；

方案4 采取文中所提出的DWG及BES捆绑式的选址定容协调优化方法.

4种方案所得的结果如表2所示.

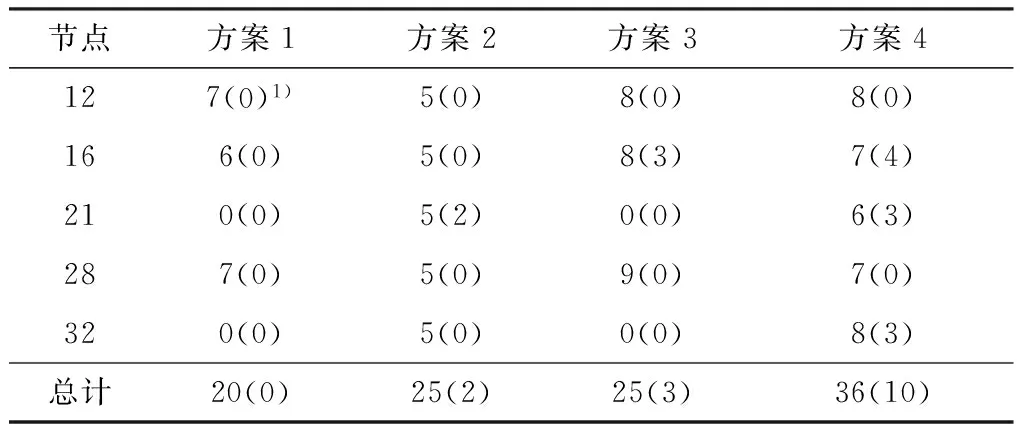
表2 4种方案

1)括号外数字代表该节点接入的DWG数目，括号内数字为该节点配置的BES模块的数目.

各方案的渗透率与年综合效益对比见表3.

表3 各方案的渗透率与年综合效益

由表3可知：方案1不考虑配置BES，因此可接纳的风电机组容量有限，等年值综合收益较低；方案2与方案3均以最大允许渗透率接入DWG，配合一定的BES可完全消纳风电，其中集中接入对BES的需求较大，而两种方案的年综合效益较方案1均有所提升；方案4考虑DWG与BES捆绑式的选址定容协调优化，通过合理配置BES提高了配电网风电的消纳能力，渗透率可提升到72%，且年综合效益最高.此外所配置的BES还能为配电网的运行提供其他辅助服务，具有潜在价值.

3.3 算法优化性能分析

为说明IMPGA用于求解文中模型的优化性能，经过50组对比测试，结果如表4所示.

由优化结果可以看出：MPGA由于对不可行解采取舍弃的方法，在趋优解集与不可行解的过渡区间较小的情况下寻优效率较低，难以搜索到最优解；而IMPGA由于自身的寻优机制，可促使种群带有一定方向性进行寻优，在此种情况下仍然表现出较高的寻优效率，且算法的稳定性有所提升.图5为一组典型的迭代曲线对比，由图5可知，与标准的MPGA相比，由于引入了所提出的寻优机制，IMPGA的寻优能力获得了大幅度的提升，能够快速利用进化方向的指引搜索最优解，加快收敛速度.

表4 算法优化结果对比

图5 算法性能对比

4 结论

文中以等年值综合收益最大化为目标建立DWG与BES的选址定容协调优化模型，分析了DWG与BES并网对系统不确定性的影响规律，在此基础上引入寻优机制对MPGA算法进行改进，从而实现模型的高效求解.根据算例仿真获得如下结论：

1)文中提出的协调优化模型可对DWG与BES的位置与容量进行综合优化配置，优化配置结果表明文中模型优化得到的方案可获得更为可观的等年值综合收益.

2)通过对DWG与BES合理的选址定容可有效提高配电网对风电的消纳能力，最大限度地利用可再生能源，DWG与BES选址定容的协调优化是适应电力系统低碳化发展趋势的配置方法.

3)文中所提出的IMPGA用于求解文中模型时具有较优的寻优性能，说明所引入的协调优化寻优机制对算法的改进是有效的.

[1] 娄素华,吴耀武,崔艳昭.电池储能平抑短期风电功率波动运行策略 [J].电力系统自动化,2014,38(2):17-22，58. LOU Su-hua,WU Yao-wu,CUI Yan-zhao.Operation strategy of battery energy storage system for smoothing short-term wind power fluctuation [J].Automation of Electric Power Systems,2014,38(2):17-22，58.

[2] AMMAR M,JOOS G.A short-term energy storage system for voltage quality improvement in distributed wind power [J].IEEE Transactions on Energy Conversion,2014,29(4):997-1007.

[3] 张节潭,程浩忠,姚良忠,等.分布式风电源选址定容规划研究 [J].中国电机工程学报,2009,29(16):1-7. ZHANG Jie-tan,CHENG Hao-zhong,YAO Liang-zhong,et al.Study on siting and sizing of distributed wind gene-ration [J].Proceedings of CSEE,2009,29(16):1-7.

[4] 张沈习,李珂,程浩忠,等.主动管理模式下分布式风电源选址定容规划 [J].电力系统自动化,2015,39(9):208-214. ZHANG Shen-xi,LI Ke,CHENG Hao-zhong,et al.Siting and sizing planning of distributed wind generators under active management mode [J].Automation of Electric Power Systems,2015,39(9):208-214.

[5] LAMAINA P,SARNO D,SIANO P,et al.A model for wind turbines placement within a distribution network acquisition market [J].IEEE Transactions on Industrial Informatics,2015,11(1):210-219.

[6] 谢石骁,杨莉,李丽娜.基于机会约束规划的混合储能优化配置方法 [J].电网技术,2012,36(5):79-84. XIE Shi-xiao,YANG Li,LI Li-na.A chance constrained programming based optimal configuration method of hybrid energy storage system [J].Power System Technology,2012,36(5):79-84.

[7] 向育鹏,卫志农,孙国强,等.基于全寿命周期成本的配电网蓄电池储能系统的优化配置 [J].电网技术,2015,39(1):264-270. XIANG Yu-peng,WEI Zhi-nong,SUN Guo-qiang,et al.Life cycle cost based optimal configuration of battery energy storage system in distribution network [J].Power System Technology,2015,39(1):264-270.

[8] ZHENG Yu,DONG Zhao-yang,LUO Feng-ji,et al.Optimal allocation of energy storage system for risk mitigation of DISCOs with gigh renewable penetrations [J].IEEE Transactions on Power Systems,2014,29(1):212-220.

[9] 尤毅,刘东,钟清,等.主动配电网储能系统的多目标优化配置 [J].电力系统自动化,2014,38(18):46-52. YOU Yi,LIU Dong,ZHONG Qing,et al.Multi-objective optimal placement of energy storage systems in an active distribution network [J].Automation of Electric Power Systems,2014,38(18):46-52.

[10] 刘舒,李正力,王翼,等.含分布式发电的微电网中储

能装置容量优化配置 [J].电力系统保护与控制,2016,44(3):78-84. LIU Shu,LI Zheng-li,WANG Yi,et al.Optimal capacity allocation of energy storage in micro-grid with distributed generation [J].Power System Protection and Control,2016,44(3):78-84.

[11] 刘文霞,牛淑娅,石道桂,等.考虑运行策略及投资主体利益的主动配电系统储能优化配置 [J].电网技术,2015,39(10):2697-2704. LIU Wen-xia,NIU Shu-ya,SHI Dao-gui,et al.Optimal allocation of ADS battery energy storage considering ope-ration strategy and investment subject benefit [J].Power System Technology,2015,39(10):2697-2704.

[12] 唐念,夏明超,肖伟栋,等.考虑多种分布式电源及其随机特性的配电网多目标扩展规划 [J].电力系统自动化,2015,39(8):45-52. TANG Nian,XIA Ming-chao,XIAO Wei-dong,et al.Multi-objective expansion planning of active distribution systems considering distributed generator types and uncertainties [J].Automation of Electric Power Systems,2015,39(8):45-52.

[13] 吴万禄,韦钢,谢丽蓉,等.含分布式电源与充电站的配电网协调规划 [J].电力系统保护与控制,2014,42(15):65-73. WU Wan-lu,WEI Gang,XIE Li-rong,et al.Coordinated planning of distribution network containing charging station and distributed generation [J].Power System Protection and Control,2014,42(15):65-73.

[14] 杨家豪,欧阳森,吴裕生,等.计及风-储联合系统概率模型的配电网随机潮流 [J].电网技术,2016,40(1):234-241. YANG Jia-hao,OUYANG Sen,WU Yu-sheng,et al.Stochastic power flow of distribution network considering probability model of wind-storage combined systems [J].Power System Technology,2016,40(1):234-241.

[15] 王成山,郑海峰,谢莹华,等.计及分布式发电的配电系统随机潮流计算 [J].电力系统自动化,2005,29(24):39-44. WANG Cheng-shan,ZHENG Hai-feng,XIE Ying-hua,et al.Probabilistic power flow containing distributed generation in distribution system [J].Automation of Electric Power Systems,2005,29(24):39-44.

[16] 盛四清,王浩.用于配电网规划的改进遗传算法 [J].电网技术,2008,32(17):69-72,83. SHENG Si-qing,WANG Hao.An improved genetic algorithm for distribution network planning [J].Power System Technology,2008,32(17):69-72,83.

Coordinated Optimal Allocation of Distributed Wind Generator and Battery Energy Storage in Distribution Network

OUYANGSenCHENXin-huiYANGJia-hao

(School of Electric Power∥Key Laboratory of Clean Energy Technology of Guangdong Province,South China University of Technology, Guangzhou 510640, Guangdong, China)

The location and capacity of distributed wind generator (DWG) and the battery energy storage (BES) both affect the operating state of the distribution system. In order to improve the wind power accommodation capacity of the distribution system and weaken the effect of wind power output uncertainty, a coordinated optimal allocation for the locating and sizing of DWG and BES is performed in the planning stage. Then, a chance-constrained programming model, of which the objective function is to maximize the annual comprehensive income, is established by taking into consideration the stochastic power flow of the wind-storage system to reflect the operating state and the uncertainty of the distribution system containing DWG and BES. Moreover, an improved multi-population genetic algorithm is proposed, and an effective searching optimal mechanism is introduced to enhance the perfor-mance of the algorithm. Simulated results on the IEEE 33-bus distribution system show that the proposed optimization model is rational and that the proposed algorithm is effective.

distribution network; distributed wind generator; battery energy storage; locating and sizing; coordinated optimization; stochastic power flow

2016-03-18

广东省自然科学基金资助项目(2016A030313476) Foundation item: Supported by the Natural Science Foundation of Guangdong Province(2016A030313476)

欧阳森(1974-)，男，博士，副研究员，主要从事电能质量、节能技术与智能电器研究.E-mail：ouyangs@scut.edu.cn

1000-565X(2017)04-0030-07

TM 711

10.3969/j.issn.1000-565X.2017.04.005