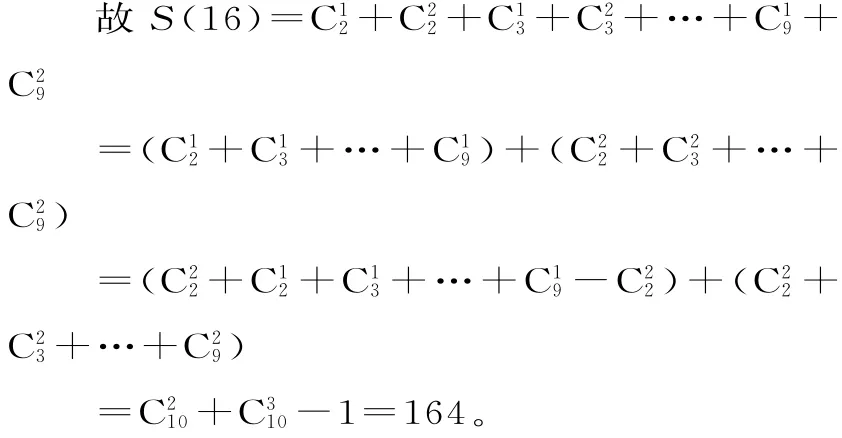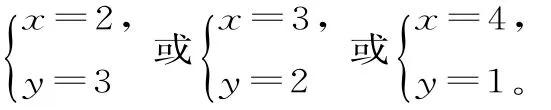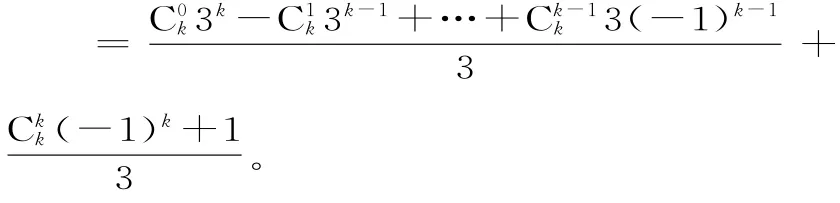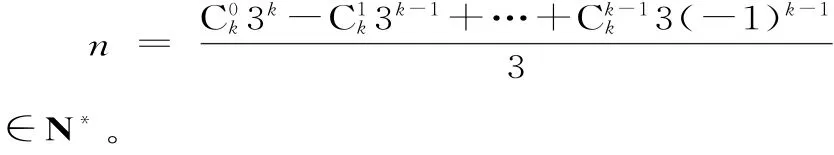全国名校排列组合问题测试

2017-06-19河南师范大学附属中学孟召臣

中学生数理化(高中版.高二数学) 2017年5期

关键词：白球红球个数

■河南师范大学附属中学孟召臣

全国名校排列组合问题测试

■河南师范大学附属中学孟召臣

一、选择题(本大题共12小题,每小题5分,共60分,每小题只有一个选项符合题意。)

1.集合A={1,2,3,4,5},B= {(x,y)x∈A,y∈A},则集合B中元素的个数为( )。

A.5 B.15 C.20 D.25

2.已知两条异面直线a,b上分别有5个点和8个点,则这13个点可以确定不同的平面个数为( )。

A.40 B.16 C.13 D.10

3.已知C7n+1-C7n=C8n,则n等于( )。

A.14 B.12 C.13 D.15

4.已知集合A={1,2,3,4},B= {5,6,7},C={8,9}。现在从这3个集合中取出2个集合,再从这2个集合中各取出1个元素,组成一个含有2个元素的集合,则一共可以组成的集合个数为( )。

A.24 B.36 C.26 D.27

5.某学校在冬季运动会的开幕式上要穿插5个小节目,其中高一、高二年级各准备2个节目,高三年级准备1个节目,则同一年级的节目不相邻的安排种数为( )。

A.56 B.48 C.36 D.24

6.已知某动点在平面直角坐标系第一象限的整点上运动(含x,y正半轴上的整点),其运动规律为(m,n)→(m+1,n+1)或(m, n)→(m+1,n-1)。若该动点从原点出发,经过6步运动到点(6,2),则不同的运动轨迹有( )。

A.15种 B.14种

C.9种 D.103种

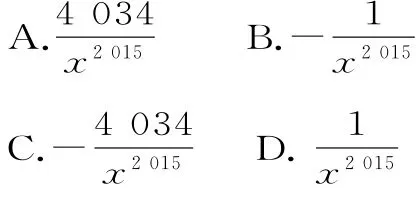
8.过三棱柱任意两个顶点作直线,其中异面直线有( )对。

A.18 B.24 C.30 D.36

A.23023B.-23023

C.-23024D.23024

10.如图1所示,在杨辉三角中,斜线AB上方箭头所示的数组成一个锯齿形的数列:1,2, 3,3,6,4,10,…,记这个数列的前n项和为S(n),那么S(16)等于( )。

A.144 B.146 C.164 D.461

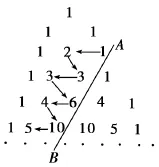
图1

11.有3对夫妇去看电影,6个人坐成一排,若女性的邻座只能是其丈夫或其他女性,则不同的坐法的种数为( )。

A.54 B.60 C.66 D.72

12.集合A={(x1,x2,x3,x4,x5)|xi∈{-1,0,1},i=1,2,3,4,5},那么集合A中满足条件”的元素个数为( )。

A.60 B.90 C.120 D.130

二、填空题(本大题共4小题,每小题5分,共20分。)

13.北京市某中学要把9台型号相同的电脑送给西部地区的3所希望小学,每所小学至少得到2台,共有____种不同送法。

15.学生的语文、数学成绩均被评定为三个等级,依次为“优秀”、“合格”、“不合格”。若学生甲的语文、数学成绩都不低于学生乙,且其中至少有一门成绩高于乙,则称“学生甲比学生乙成绩好”。如果一组学生中没有哪位学生比另一位学生成绩好,并且不存在语文成绩相同、数学成绩也相同的两位学生,那么这组学生最多有____人。

16.如图2是一个正方体纸盒的展开图,若把1,2,3,4,5,6分别填入小正方形后,按虚线折成正方体,则所得到的正方体相对面上的两个数的和都相等的概率是____。

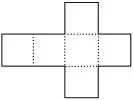
图2

三、解答题(解答应写出文字说明、证明过程或演算步骤,共70分。)

17.(本小题满分10分)一个口袋内有4个不同的红球,6个不同的白球。

(1)从中任取4个球,红球的个数不比白球少的取法有多少种?

(2)若取一个红球记2分,取一个白球记1分,从中任取5个球,使总分不少于7分的取法有多少种?

18.(本小题满分12分)若(x2-3x+2)5=a0+a1x+a2x2+…+a10x10。

(1)求a1+a2+…+a10。

(2)求(a0+a2+…+a10)2-(a1+a3+…+a9)2。

19.(本小题满分12分)已知集合A= {x|1

(1)从A∪B中取出3个不同的元素组成三位数,则可以组成多少个?

(2)从集合A中取出1个元素,从集合B中取出3个元素,可以组成多少个无重复数字且比4000大的自然数?

20.(本小题满分12分)已知等差数列2, 5,8,…,与等比数列2,4,8,…,求两数列中公共项按从小到大的顺序排列构成新数列{cn} 的通项公式。

21.(本小题满分12分)求证:当n∈N*时

22.(本小题满分12分)已知集合A= {a1,a2,a3,a4},B={0,1,2,3},f是从A到B的映射。

(1)若B中每一个元素都有原象,则不同的映射f有多少个?

(2)若B中的元素0无原象,则不同的映射f有多少个?

(3)若f满足f(a1)+f(a2)+f(a3)+ f(a4)=4,则不同的映射f又有多少个?

1.D

2.C 提示:分两类:第一类,直线a与直线b上8个点可以确定8个不同的平面;第二类,直线b与直线a上5个点可以确定5个不同的平面。故可以确定8+5=13(个)不同的平面。

3.A 提示:因为C7n+1=C8n+1,则7+8= n+1,故n=14。

4.C 提示:C14C13+C14C12+C13C12=26。

5.B 提示:先将5个节目进行全排列,共有A55种情况,其中A1,A2相邻或B1,B2相邻的情况共有2A44A22种,A1,A2相邻并且B1,B2也相邻的情况共有A33A22A22种,故同一年级的节目不相邻的安排种数为A55-2A44A22+A33A22A22=48。

6.C 提示:由运动规律可知,每一步的横坐标都增加1,而纵坐标每一步增加1或减少1。经过6步变化后,结果由0变到2,因此这6步中有2步是按照(m,n)→(m+1,n-1)运动的,有4步是按照(m,n)→(m+1, n+1)运动的,因此,共有C26=15(种)走法,而此动点只能在第一象限的整点上运动(含x,y正半轴上的整点),当第一步(m,n)→(m+1,n-1)时不符合要求,有C15种;当第一步(m,n)→(m+1,n+1),但第二、三两步为(m,n)→(m+1,n-1)时也不符合要求,有1种,故要减去不符合条件的C15+1=6 (种),故共有15-6=9(种)运动轨迹。

7.A 提示:由条件知,(a-1)2017=1,则a=2。展开式的第2017项为T2017=4034x-2015。

8.D 提示:三棱柱共6个顶点,由此6个顶点可组成C46-3=12(个)不同四面体,而每个四面体有3对异面直线,则共有12× 3=36(对)异面直线。

10.C 提示:由题图知,数列中的首项是C22,第2项是C12,第3项是C23,第4项是C13,…,第15项是C29,第16项是C19。

11.B 提示:记3位女性为a、b、c,其丈夫依次为A、B、C。当3位女性都相邻时可能情形有两类:第一类男性在两端(如BAabcC),有2A33种,第二类男性在一端(如 XXAabc),有2A22A33种,共有A33(2A22+2)= 36(种)。当仅有两位女性相邻时也有两类,第一类这两人在一端(如abBACc,第二类这2人两端都有其他人(如AabBCc),共有4A23= 24(种),故坐法共有36+24=60(种)。

因此,10+40+80=130,故答案为D。

13.10

15.3 提示:假设满足条件的学生有4位或4位以上,设其中4位同学分别为甲、乙、丙、丁,则4位同学中必有2位同学语文成绩一样,且这2个人数学成绩不一样,那么这2个人中一个人的成绩比另一个人好,故满足条件的学生不能超过3人。当有3位学生时,用A,B,C表示“优秀”、“合格”、“不合格”,则满足题意的。

17.(1)将取出4个球分成三类情况:

1)取4个红球,没有白球,有C44种;

2)取3个红球1个白球,有C34C16种;

3)取2个红球2个白球,有C24C26种。

故有C44+C34C16+C24C26=115(种)方法。