基于干扰观测器与模糊前馈补偿的随动系统PID控制策略

姜 尚，田福庆，梁伟阁，潘林豪，杨 波

(海军工程大学 兵器工程系，湖北 武汉 430033)

基于干扰观测器与模糊前馈补偿的随动系统PID控制策略

姜 尚，田福庆，梁伟阁，潘林豪，杨 波

(海军工程大学 兵器工程系，湖北 武汉 430033)

针对随动系统在非线性随机力矩干扰时输出信号易畸变的现象，提出一种基于干扰观测器与模糊前馈补偿的随动系统PID控制策略。在随动系统“三闭环”结构模型的基础上，合理设计干扰观测器与模糊前馈补偿器，对干扰力矩的不确定性误差进行补偿，经仿真试验与结果分析，与传统模糊PID控制策略相比，所提策略能更好地补偿随动系统在非线性随机力矩干扰下的不确定性误差，削弱模糊PID控制的抖振，使系统具有良好的跟踪性能与鲁棒性。

控制理论；随动系统；干扰观测器；模糊控制；前馈补偿

随着当代科技迅猛发展，随动系统得到广泛应用，在其运行过程中，被控对象(电机主轴等重要装置)随时可能遭受外部施加的未知干扰力矩，它所造成的不确定性误差是影响系统跟踪控制性能的主要原因[1]。对此，在传统的控制系统中通常采用模糊PID策略加以抑制。模糊PID控制策略应用较广泛、技术较成熟，但它存在对外部干扰适应能力差等明显问题，已不能满足高控精度需求，特别是难以有效地应用于时变系统。

模糊前馈控制使随动系统具有良好的鲁棒性，能够对外部施加的非线性随机干扰力矩造成的不确定性误差进行有效补偿；干扰观测器结构简洁、抑制干扰性能突出，两者均应用广泛。王修岩等[2]在传统速度前馈补偿的基础上引入干扰观测器，提高系统对干扰力矩的抑制能力；陆建山等[3]利用改进型干扰观测器提高稳定平台随动系统对扰动的抑制性能；王珏等[4]基于模糊PID光电跟踪系统前馈补偿的控制策略，降低干扰力矩对控制精度的影响。但在非线性随机力矩的干扰下，两者的缺陷暴露：模糊控制依赖设计的经验，规则库不完整，导致控制精度受限，系统易抖振；干扰观测器对非建模动态和系统模型不确定性的控制效果并不理想。

为解决上述问题，提出一种基于干扰观测器与模糊前馈补偿的随动系统PID控制策略，补偿非线性随机力矩干扰下的不确定性误差，经仿真分析，验证了所提策略的实用性和有效性。

1 建立随动系统模型

对直流力矩电机与PWM放大电路建模，加上电流、速度及位置环后，构成三环控制驱动模型；在分析模糊前馈补偿与干扰观测器原理的基础上设计得到基于干扰观测器与模糊前馈补偿的随动系统“三闭环”结构模型，如图1所示。

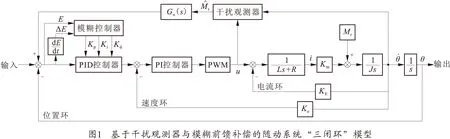
模型由内至外分别为电流环、速度环与位置环，被控对象采用双环控制结构[5](速度环与电流环)，位置环采用PID控制，速度环采用PI控制，PWM近似为比例环节。

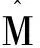
2 基于模糊PID的前馈补偿控制

2.1 模糊PID控制

常规二维模糊PID控制原理[7]如图2所示。

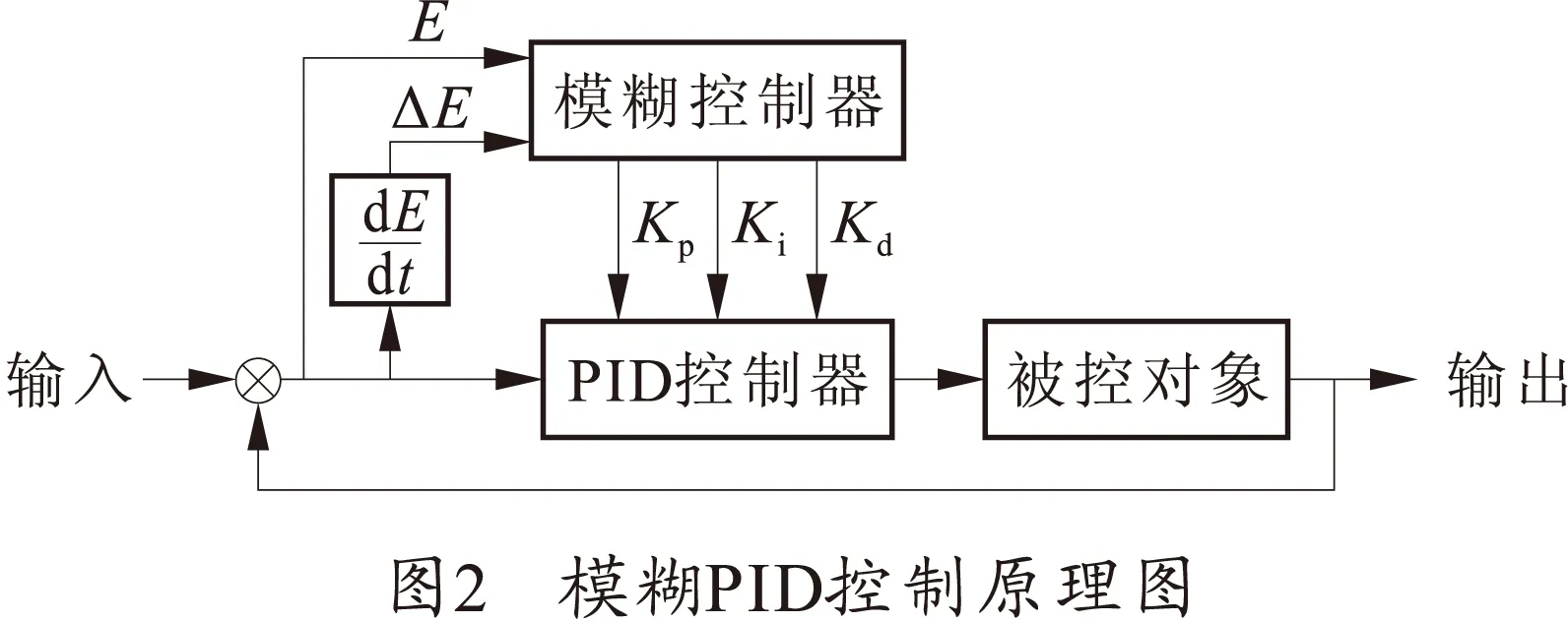
模糊控制的核心是总结设计者的模糊规则，本系统使用的3个模糊控制模块均为两输入一输出，输入量为误差E与误差变化率ΔE；输出量分别为Kp、Ki、Kd。为确保各变量的基本论域均能较好地被模糊集覆盖，设定输入量与输出量的论域：E为 {-1，1}，ΔE为{-40，40}，Kp为 {-15.1，15.1}，Ki为{-5，5}，Kd为{-0.1，0.1}。

为提高控制器的控制精度，将输入量与输入量在论域区间上的模糊子集均定义为{负大(NB)、负中(NM)、负小(NS)、零(ZO)、正小(PS)、正中(PM)、正大(PB)}7个语言值。各模糊控制规则如表1～3所示。

表1 Kp模糊控制规则

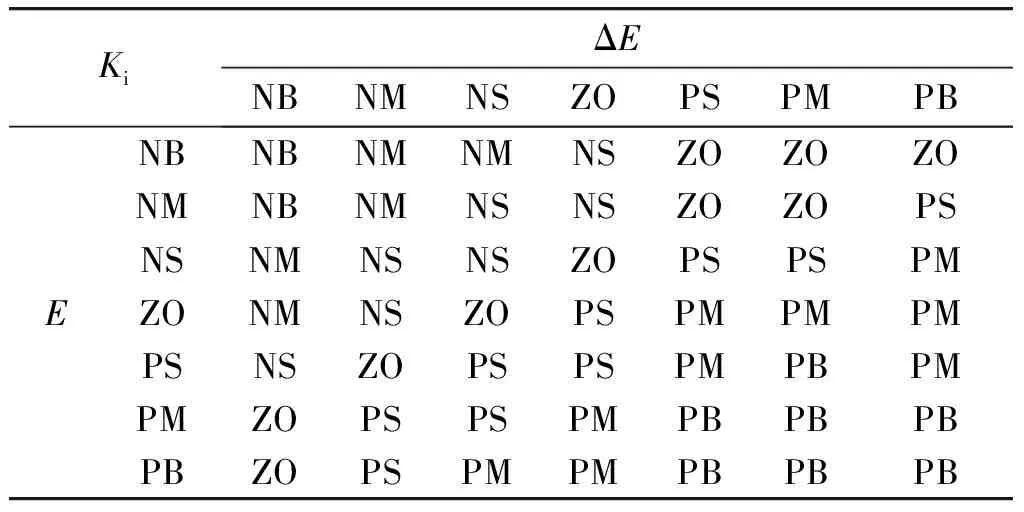
表2 Ki模糊控制规则

表3 Kd模糊控制规则

建立模糊控制规则，需遵循两条原则[8]：

1)当误差为正的较大值且误差变化率为正值时，输出应为较大正值，以尽快减小误差。

2)当误差为正的较大值但误差变化率为负值时，输出应为较小正值或为0。

PID控制调整式为

Kp(k)=Kp0(k-1)+ΔKp(k)

(1)

Ki(k)=Ki0(k-1)+ΔKi(k)

(2)

Kd(k)=Kd0(k-1)+ΔKd(k)

(3)

式中：Kp0(k-1)，Ki0(k-1)，Kd0(k-1)为上一时刻的PID参数值；Kp(k)，Ki(k)，Kd(k)为当前参数值；ΔKp(k)、ΔKi(k)、ΔKd(k)为模糊控制器的输出值。

2.2 前馈补偿原理

前馈补偿可大幅减小系统的稳态误差，对抑制系统外的力矩干扰十分有效，原理如图3所示。

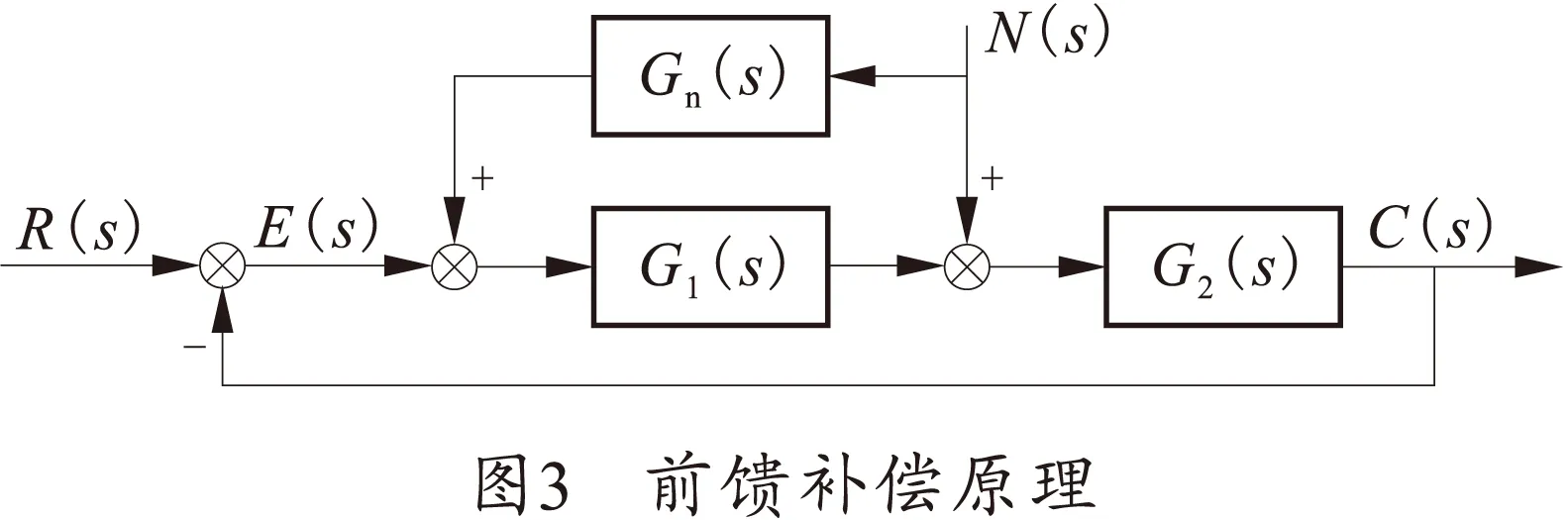
图3中，N(s)是随动系统外部施加的干扰力矩，G1(s)、G2(S)为前向通路传递函数，Gn(s)为前馈补偿传递函数，通过恰当设计Gn(s)使其对输出G(s)进行补偿，以抵消外部干扰N(s)由G2(S)对输出C(s)的影响。

根据经典自动控制原理的系统分析方法，可得外部干扰N(s)产生的误差量为

(4)

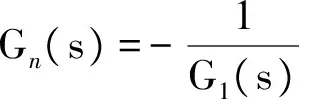
由于随动系统的前向通路传递函数包含着模糊PID控制环节，Kp、Ki、Kd等参数值随系统误差的变化而变化，故Gn(s) 也随之变化，结合图1，根据比较点移动规则将速度与电流反馈移至外部力矩扰动输入后，其传递函数为G2(s)。

设PI速度调节器的传递函数为

(5)

由式(5)求出Gn(s)的传递函数为

(6)

式中：Kp，v、Ki，v分别为PI速度调节器的比例、积分系数；Kpwm为PWM逆变器近似为比例环节时的比例系数；Km为电机力矩常数。

Gn1(s)的状态空间可表示为

(7)

Gn2(s)的具体公式为

(8)

3 干扰观测器的设计

在随动系统闭环结构的基础上合理设计干扰观测器，能增强对外部干扰的抑制作用，并且干扰观测器的稳定性和误差不确定性可控制在较低范围内。

干扰观测器的设计实际可转化为合理设计低通滤波器Q(s)与名义模型Pn(s)。通过对系统中各环节的推导可得被控对象的名义模型Pn(s)[9]，干扰观测器于速度环处引入，Pn(S)实际上为速度环的控制对象，推导得到干扰观测器的设计框图，如图4所示。

可将电流环简化成一阶模型，并将给定速度和反馈时的滤波环节包含至速度环的内部，由前面各环节的数学模型，推导出名义模型为

(9)

按设计低通滤波器的方法设计Q(s)，为使随动系统获得较好的跟踪性能，1-Q(s)应该在频谱低频段的曲线尽量陡，此时Q(s)在高频段的曲线较为平缓，使系统对干扰力矩的抑制能力下降。故常选取Q(s)的高频特性与1-Q(s)的低频特性相对称的函数

(10)

(11)

式中：aNk为二项式系数；N为Q(S)的阶次；τ为Q(s)的时间常数。

Q(s)的相对阶次增大会导致其幅值过高，系统在谐振频率附近的鲁棒性降低，且结构较复杂；Q(s)的阶次和相对阶次均应尽量小，故其结构应尽量简洁，选取常用的Q(s)结构[10]为

(12)

系统低频性能与τ成反相关关系，τ越小，对外部力矩干扰的抑制能力越强，但高频时较平缓，抑制能力下降；τ越大，情况相反，故选取τ时要综合考虑控制系统的性能要求。通常，τ为采样时间的10～ 15倍，在本系统中，选取τ为0.000 1，故低通滤波器为

(13)

4 仿真与分析

4.1 仿真实验

在随动系统“三闭环”结构模型的基础上，根据干扰观测器与模糊前馈补偿的原理与设计方法，在Simulink中搭建基于干扰观测器与模糊前馈补偿的随动系统PID仿真模型，如图5所示。

设定系统仿真参数：L≈0，R= 8Ω，J=0.465N·m，Km=6N·m/A，Ke=0.16V/(rad·s-1)，KE=0.11V/(rad·s-1)；PID参数初始值为Kp 0=120，Ki 0=8，Kd 0=5；PI的参数Kp，v=10,Ki，v=1；PWM可近似为比例环节，KPWM=10；随机非线性干扰力矩为My=A·sin(0.84t)N·m,A为 [-3.89，3.89]区间内的随机数[11]。

其中，“FuzzyControl”部分为模糊控制器仿真模型，根据式(7)编写S函数实现其状态空间方程，并由已设定的参数可得：

(14)

“Observer”部分为干扰观测器仿真模型，由已设定的参数可得

(15)

4.2 结果分析

首先，以单位阶跃信号作为系统的输入信号，以振幅随机的正弦信号作为外部施加于电机主轴的干扰力矩，模拟舰炮随动系统在大角度调转时受海浪波动力矩干扰下的工况，分别运行模糊PID和基于干扰观测器与模糊前馈补偿的PID控制策略仿真模型，得到位置曲线与误差曲线，如图6所示。

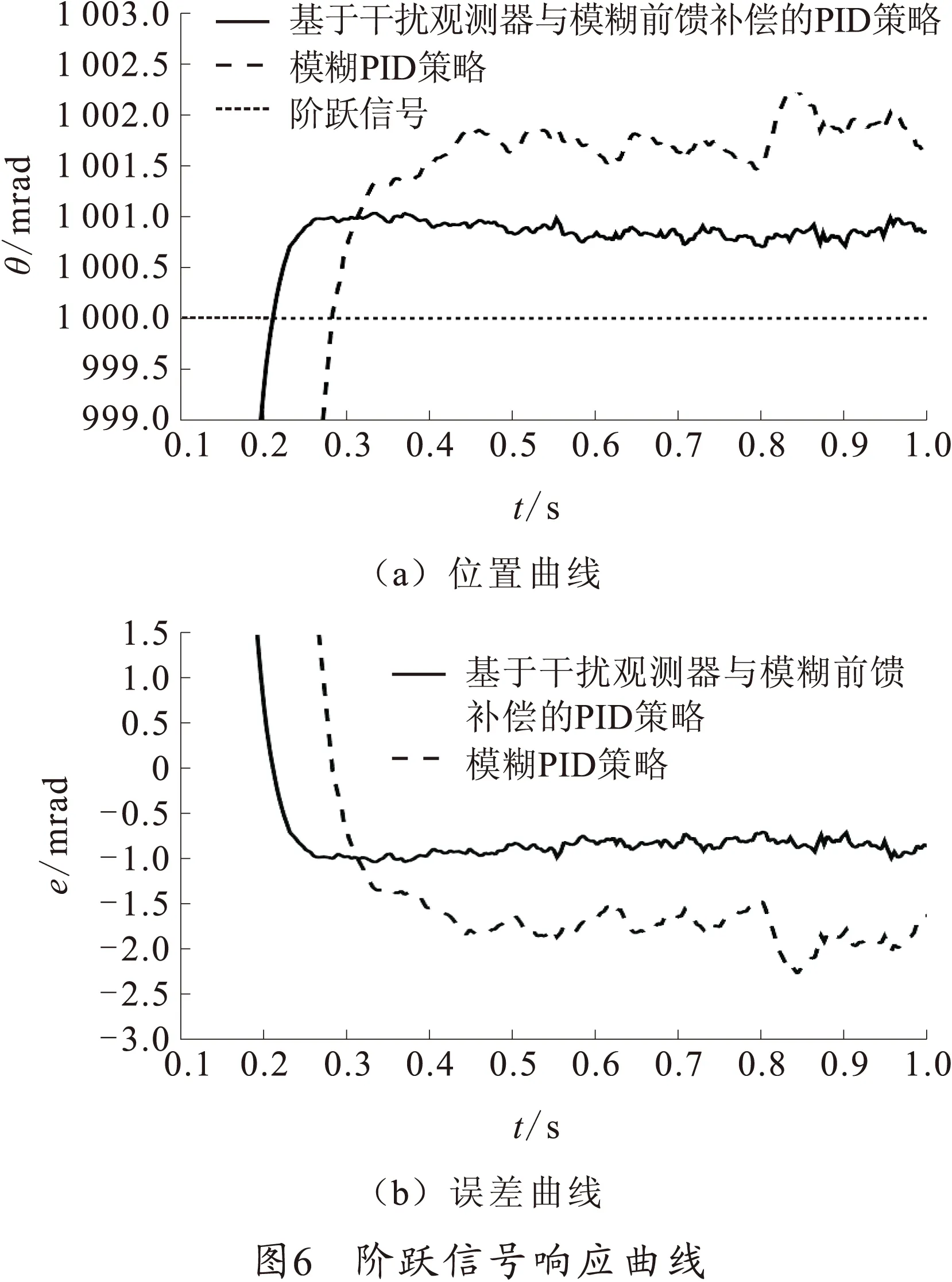
系统在跟踪单位阶跃信号时，两种控制策略均能使跟踪位置值与误差值较快地趋于稳定，但前者在调控过程中PID抖振幅度较大，后者使系统表现出更强的快速性、稳定性和干扰抑制能力，削弱了PID控制的抖振，验证了所提控制策略使随动系统具有良好的阶跃跟踪能力。

随后，以单位斜坡信号作为系统的输入信号，外部施加于电机主轴的干扰力矩同上，模拟舰炮随动系统在等速跟踪目标时受海浪波动力矩干扰下的工况，分别运行两种控制策略的仿真模型，得到位置曲线与误差曲线，如图7所示。

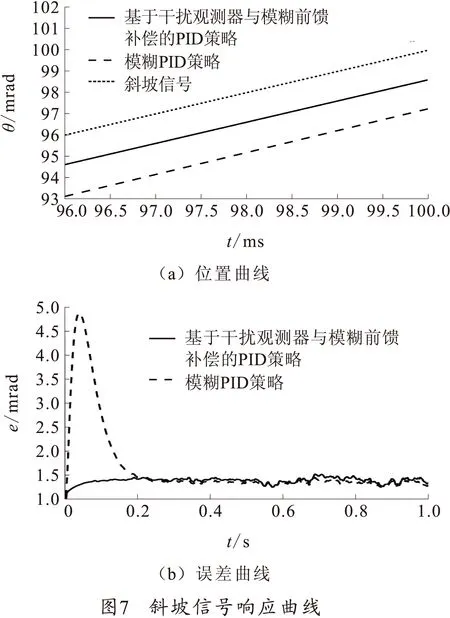
系统在跟踪单位斜坡信号时，两种控制策略均使系统实现了较快的等速跟踪，但前者在初期使系统出现较大的误差波动，后者的跟踪误差始终稳定在较低范围内，使系统表现出更强的鲁棒性和抑制干扰力矩的能力，验证了所提策略使系统具有良好的斜坡跟踪能力。

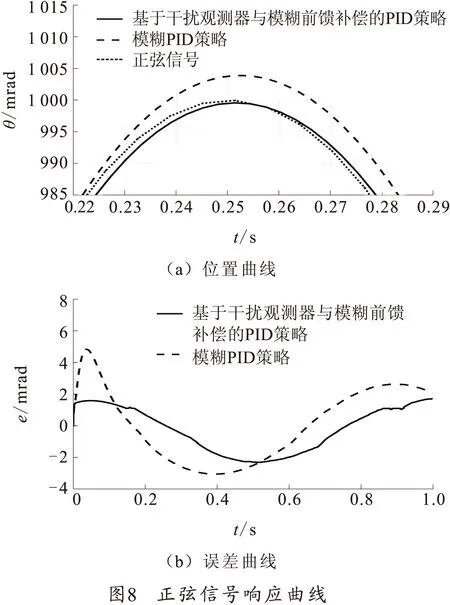
最后，以单位正弦信号sin 2πt输入信号，外部施加于电机主轴的干扰力矩同上，模拟舰炮随动系统在加速、减速跟踪目标时受海浪波动力矩干扰下的工况，分别运行两种控制策略的仿真模型，得到位置曲线与误差曲线，如图8所示。

系统跟踪正弦信号时，前者跟踪位置曲线偏离输入信号较大，且误差值较大，而后者位置曲线紧紧跟随输入信号，始终将误差值控制在较小范围内，使系统表现出更强的稳定性和干扰抑制能力，验证所提策略使系统具有良好的正弦跟踪能力。

综上所述，相比传统模糊PID控制策略，所提策略在跟踪阶跃、斜坡和正弦3类输入信号时，均能使系统表现出更佳的鲁棒性、稳定性及抑制干扰力矩的能力，并在一定程度上削弱了PID控制的抖振，验证了所提策略具有良好的信号跟踪能力。

5 结束语

笔者以随动系统“三闭环”结构为基础，提出基于干扰观测器与模糊前馈补偿的PID控制策略，采用干扰观测器快速观测外部干扰力矩，利用模糊前馈补偿增强系统的跟踪性能，对非线性随机干扰力矩的不确定性误差进行有效补偿，经仿真分析，验证了所提控制策略的有效性与实用性。

References)

[1]李涛，刘琮敏，侯立国，等．供弹机模糊自适应PID控制器设计[J]．火炮发射与控制学报，2009(3)：47-51． LI Tao，LIU Congmin，HOU Liguo，et al．Fuzzy adaptive PID controller design of feeder[J]．Journal of Gun Launch & Control，2009(3)：47-51．(in Chinese)

[2]于哲，苏剑波．基于干扰观测器的不确定性多变量系统控制[J]．自动化学报，2014，40(11)：2643-2649． YU Zhe，SU Jianbo. Disturbance observer based control for linear multi-variable systems with uncertainties[J]. Acta Automatica Sinica，2014，40(11)：2643-2649.(in Chinese)

[3]王修岩，谷新铭，李宗帅．基于干扰观测和前馈补偿的电动加载复合控制[J]．制造与自动化，2015，37(1)：11-14． WANG Xiuyan，GU Xinming，LI Zongshuai．Electric loa-ding composite control based on disturbance observer and feed-forward compensation[J]．Journal of Manufacturing and Automation，2015，37(1)：11-14．(in Chinese)

[4]陆建山，王昌明，何云峰．改进型干扰观测器在稳定平台伺服系统中的应用[J]．振动与冲击，2013，2(8)：96- 99． LU Jianshan，WANG Changming，HE Yunfeng．Application of improved disturbance observer in a stable platform servo system[J]．Journal of Vibration and Shock，2013，2(8)：96-99．(in Chinese)

[5]王珏，田福庆．基于模糊PID的光电跟踪系统自适应前馈补偿控制[J]．舰船电子工程，2014，34(11)：169-173．WANG Jue，TIAN Fuqing．Feedforward compensation control of optoelectronic tracking system based on fuzzy PID[J]．Ship Electronic Engineering，2014，34(11)：169-173．(in Chinese)

[6]HILKERT J M．Inertially stabilized platform technology concepts and principles[J]．Control Systems IEEE, 2008, 28(1)：26-46.

[7]陈益，薄煜明，邹卫军．模糊自适应PID控制在高精度光电跟踪伺服系统中的应用[J]．火炮发射与控制学报，2008(12)：33-36． CHEN Yi，BO Yuming，ZOU Weijun．Application of adaptive fuzzy-PID control in high accuracy optoelectronic tracking servo system[J]．Journal of Gun Launch & Control，2008(12)：33-36．(in Chinese)

[8]侯宏录． 模糊PID控制在光电跟踪控制系统中的应用[J]．光电工程，2006，33(5)：12-16． HOU Honglu．Application of fuzzy-PID control in system of photo-electric tracking[J]．Opto-Electronic Engineering，2006，33(5)：12-16．(in Chinese)

[9]SHIM H，JOO Y J．State space analysis of disturbance observer and a robust stability condition[C]∥46th IEEE Conference on Decision and Control. New Orleans:IEEE，2007：2193-2198．

[10]秦金义． 含干扰观测器盬永磁同步电机位置控制系统研究[D]． 哈尔滨：哈尔滨工业大学，2012． QIN Jinyi．Research on permanent magnet synchronous motor position control system with disturbance observer[D]．Harbin： Harbin Institute of Technology，2012．(in Chinese)

[11]田福庆，刘云秋，周耕书．舰炮随动系统设计原理[M]．武汉：海军工程学院，1997：161-162． TIAN Fuqing，LIU Yunqiu，ZHOU Gengshu．The design principle of naval gun servo system[M]．Wuhan：Naval Institute of Engineering，1997：161-162．(in Chinese)

PID Control Strategy of Servo System Based on Disturbance Observer andFuzzy Feed-forward Compensation

JIANG Shang, TIAN Fuqing, LIANG Weige,PAN Linhao，YANG Bo

(Department of Weaponry Engineering, Naval University of Engineering, Wuhan 430033, Hubei, China)

In the presence of nonlinear and random disturbance torque, the output signal of serve system deteriorates easily. Aiming at this phenomenon, proposed is a kind of PID control strategy of serve system based on disturbance and fuzzy feed-forward compensation. Based on the three closed loop structure model of servo system，the disturbance observer and fuzzy feed-forward are reasonably designed to compensate for the uncertain errors of disturbance torque. Through the simulation experiment and the analysis of results and in comparison with the traditional control strategy of fuzzy PID, the proposed strategy could compensate for uncertain errors better in the presence of nonlinear random torque, weaken the chattering of fuzzy PID control and make the system possess good tracking performance and robustness.

control theory; servo system; disturbance observer; fuzzy control; feed-forward compensation

2016-05-06

姜尚(1992—)，男，直博研究生，主要从事系统运用于保障工程研究。E-mail：jiangshang1992@126.com

10.19323/j.issn.1673-6524.2017.02.007

TJ81+0.376

A

1673-6524(2017)02-0029-06