航空发动机分布式系统解耦控制研究*

段进峰，彭靖波，谢寿生，王立国

（1.空军工程大学航空航天工程学院，西安 710038；2.解放军95507部队，贵阳 550000）

航空发动机分布式系统解耦控制研究*

段进峰1，彭靖波1，谢寿生1，王立国2

（1.空军工程大学航空航天工程学院，西安 710038；2.解放军95507部队，贵阳 550000）

航空发动机控制系统是一个复杂的多变量控制系统，控制变量之间的相互耦合会严重影响系统的动态、稳态性能，在发动机最大工作状态时，甚至会造成超温、超转等现象，严重威胁着飞行安全，制约着发动机性能的提高。针对上述情况，利用改进型遗传算法对航空发动机双回路PID控制参数进行寻优，实现了对控制变量的解耦。数值仿真结果表明改进方法能有效消除各变量之间的耦合影响，而且在控制精度、跟踪性能等方面表现良好，对不同环境条件下的航空发动机模型均有良好的控制效果，适用于航空发动机控制。

航空发动机，分布式控制，模拟退火，自适应遗传算法，解耦

0 引言

航空发动机控制系统［1］控制变量之间的相互耦合会严重影响系统的动、稳态性能，甚至会在发动机最大工作状态，造成超温、超转等现象［2］，严重威胁飞行安全，制约着发动机性能的提高，所以发动机控制系统设计领域一直将消除变量之间的耦合作用作为研究热点之一。

PID控制的算法简单、鲁棒性好、可靠性高，因此，得到了广泛应用［3］，但是传统PID控制也有其不足之处，如参数不易整定、自适应能力差等［4］。文献［2-3］分别利用神经网络和支持向量机在对PID参数进行整定，从而实现了发动机控制变量的解耦。但是，神经网络和支持向量机作为机器学习方法，有其必然的局限性，如神经网络存在局部最小值、过学习以及结构难以确定等问题，支持向量机存在计算量大、计算效率低等问题。文献［4-6］利用遗传算法实现了PID参数的优化整定，但都是针对单变量系统，不存在解耦问题。

针对上述发动机控制现状，本文利用改进型遗传算法对航空发动机双回路PID控制参数进行寻优，实现了对控制变量的解耦。通过数值仿真对该方法在控制精度、跟踪性能等方面进行验证。

1 基于改进遗传算法的PID解耦控制器结构原理

选取某型涡扇发动机的状态变量为低压、高压转子的转速nL、nH，输出变量为低压转子的转速nL和涡轮后燃气总温控制变量为主供油量mf和尾喷管临界面积A8，其数学模型可表示为：

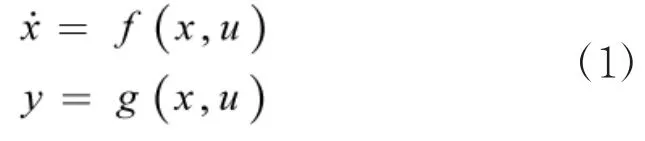
控制器采用离散增量式PID控制律：

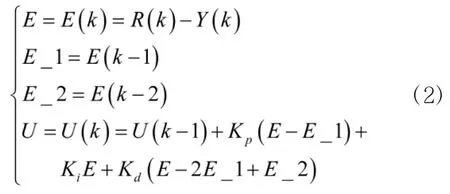
mf和A8的执行机构分别采用如下的传递函数：

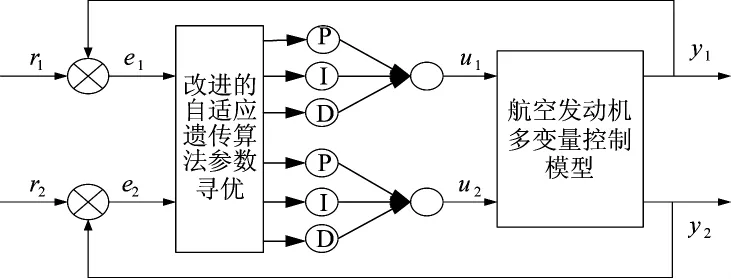
图1 基于改进遗传算法的涡扇发动机双变量PID解耦控制系统结构图

图1为基于改进遗传算法的涡扇发动机双变量PID控制系统原理图。在此控制系统中，发动机实际输出参数与参考输入的差值作为寻优系统的输入，寻优系统以误差值平方的时间积分作为目标函数，为防止超调，采用超调惩罚措施，采用改进遗传算法优化双回路的PID参数，实现对指定回路的解耦控制。

图中，r1是nL的期望值，r2是nH的期望值，u1代表mf的变化量，u2代表A8的变化量，y1代表nL的实际值，y2代表T5的实际值。

2 改进自适应遗传算法

自适应遗传算法［7-8］通过自适应调整交叉、变异概率，在保持群体多样性的同时能够有效保护优良模式，保证了遗传算法的收敛性；通过引入模拟退火算法［9］将拉伸变换后的适应度函数加入自适应遗传算法中，对自适应交叉、变异方式及其相应概率的自适应调节方式的选择等方面，有效融合两者的优点，提高方法的快速性、准确性和自适应能力，系统流程图如图2所示：

图2 模拟自适应遗传算法流程

2.1 模拟退火拉伸适应度函数

设PID控制系统性能指标如下：

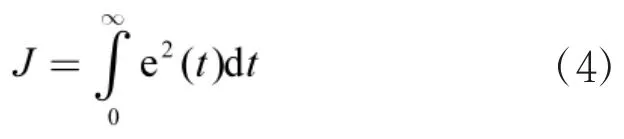
为防止超调并有效减小超调量，采用惩罚措施，即一旦产生超调，便把超调量作为性能指标的一部分，此时：

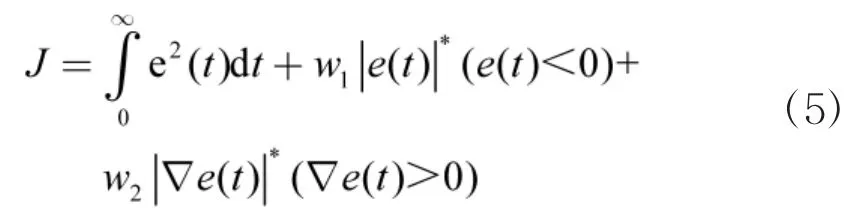
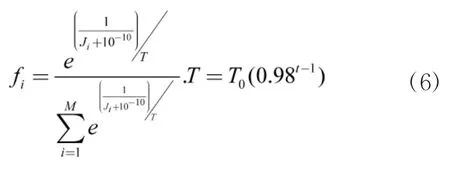
其中，fi代表第i个个体的适应度值，M代表每代种群的规模，t代表遗传算法所进行的代数，T代表假定的温度，T0代表T的初始值。通过引入温度参数并对适应度进行适当拉伸，可以保证在算法初期，适应度相近的个体产生后代的概率也相近，能够保证初期种群基因的多样性，避免过早落入局部最优解；而随着温度下降，使具有相近目标函数值的个体之间的适应度值的差异得到放大，使优秀个体的优势更加明显，使算法后期能更加快速、准确地定位到实际最优解。

2.2 模拟退火自适应遗传算法

2.2.1 选择操作

遗传算法的进化过程包括3个基本运算操作：选择、交叉、变异，并能够通过以上优化过程的不断循环来寻找到全局最优解。由于本文需要同时优化6个参数，如果采用二进制编码，若要同时保证足够的优化精度，则会使编码长度过长，并由此会带来搜索空间急剧膨胀、计算量过大的弊端。因此，本文在编码时选择浮点数编码方式，为算法提供较高精度的同时也提高了算法的计算效率。设计过程中以两组PID控制器的6个参数为被优化的参数，并设置种群的大小为M。

为了保证适应度值大的个体以相应大的概率被选入下一代个体当中，本文采用比例选择算子。则个体Xi被选中的概率与其适应度为fi的关系为：

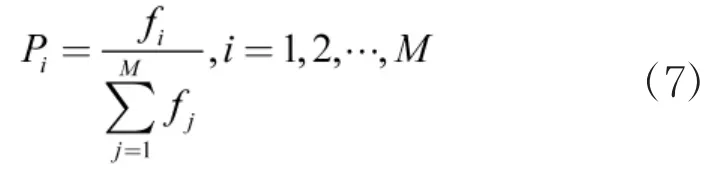
2.2.2 交叉操作

交叉运算是遗传算法产生新个体的最主要方式。本文采用随机非均匀算术交叉方式，设要进行交叉运算的2个个体分别为和所产生的2个新个体分别为：

交叉参数α是由系统随机产生的六维向量，其元素是区间［-0.2 1.2］上的随机数，由此产生的子代可以分布于更广的空间里，而不必局限于父代个体的连线上，从而避免了寻优的早熟，提高了全局最优的搜索效率。交叉概率Pc根据适应度值按以下公式自适应调整：

fmax代表整个群体中适应度的最大值，favg代表每代群体适应度的平均值，fi代表要进行交叉运算的两个个体中的比较大的适应度值，Pc1、Pc2代表自适应交叉概率的上下限，是两个常数。交叉概率的自适应调整，可以降低适应度值大的个体的交叉概率，从而保护优良的模式；而增大适应度较低的个体的交叉概率，可以减少不良个体并能有效扩大搜索空间。同时，用fmax-favg代表群体的分散程度，当群体分散程度比较低时，使Pc增大，保持群体多样性，避免陷入局部最优。

2.2.3 变异操作

变异运算可以提高遗传算法的局部搜索能力、保持种群的多样性和防止算法的早熟现象。本文选用非均匀变异方式：

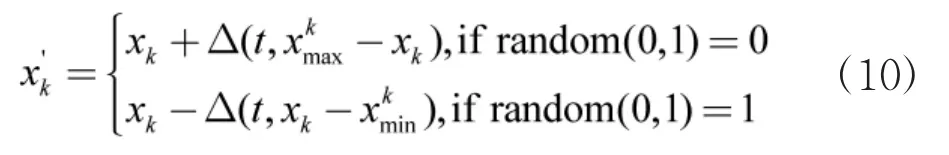
在遗传算法的运行初期，非均匀变异可以使算法进行近乎均匀的随机搜索，而在其后期，则使它进行局部搜索，从而能在希望最大的重点区域里来进行最优解的搜索。

系统的变异概率按以下公式自适应调整：

变异概率的自适应调整作用与交叉过程相类似。

2.2.4 保留最优个体策略

采用保留最优个体的策略可以在保证算法收敛的基础上使算法加快收敛速度，本文将算法每代中的最优个体挑选出来，令它不参与任何遗传运算操作。

选用前面介绍的浮点数编码、比例选择、自适应交叉、变异概率、非均匀算术交叉、非均匀变异及最优保留策略，并引入特殊目标函数以及模拟退火拉伸的适应度函数就构成了本文的改进遗传算法，从而实现回路的解耦和PID参数的优化。

3 仿真实验及案例分析

根据一般经验选取遗传算法的参数为：

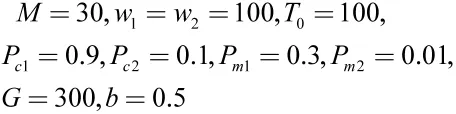
给定输入激励为单位阶跃输入，即：

在H=0 km，Ma=0中间状态时的仿真控制结果如图3、图4所示。以图3为例来看，图3（a）为改进遗传算法与普通遗传算法参数寻优过程的对比，其中曲线1代表普通遗传算法的寻优过程中目标函数的变化，曲线2代表改进后遗传算法的优化过程，可以看出，改进后遗传算法在迭代20代左右的寻优精度就已达到改进前迭代300代的优化精度，迭代60代以后，普通遗传算法的目标函数值基本未发生变化，即已经陷入了局部最优，然而改进后的遗传算法在大约迭代110代后找到最优解。可见，改进遗传算法的应用可以有效提高计算速度，避免局部最小值，从而提高控制算法的实时性和控制精度。图3（b）、图3（c）分别为最优参数下的输出量曲线和控制量曲线，由图可知，当低压转速给定值发生1%的阶跃变化，在刚开始阶段，发动机供油量迅速增大，使得发动机低压转速也迅速增大；在动态变化中后期，为了避免发生超调，发动机供油量先减小后缓慢增加至稳定值，使低压转速增加速度不断减小，最终达到给定水平。与此同时，为了消除供油量增加对涡轮后燃气温度的影响，尾喷管临界面积与供油量同步调向相反方向变化，即供油量迅速增大时尾喷管临界面积迅速减小。发动机通过同时调节供油量和尾喷管临界面积，使低压转速迅速上升至给定值，涡轮后燃气温度在发生微小偏离后也迅速回归其给定水平。此控制系统调节时间在1.5 s内，不存在超调量，2 s后即基本消除了稳态误差，控制量在可接受范围内，系统在拥有良好的动、稳态特性的基础上，很好地实现了变量间的解耦。

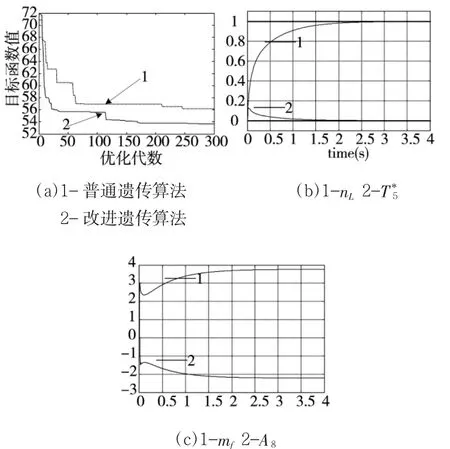
图3 H=0 km，Ma=0低压转子转速为阶跃输入时的解耦仿真控制曲线

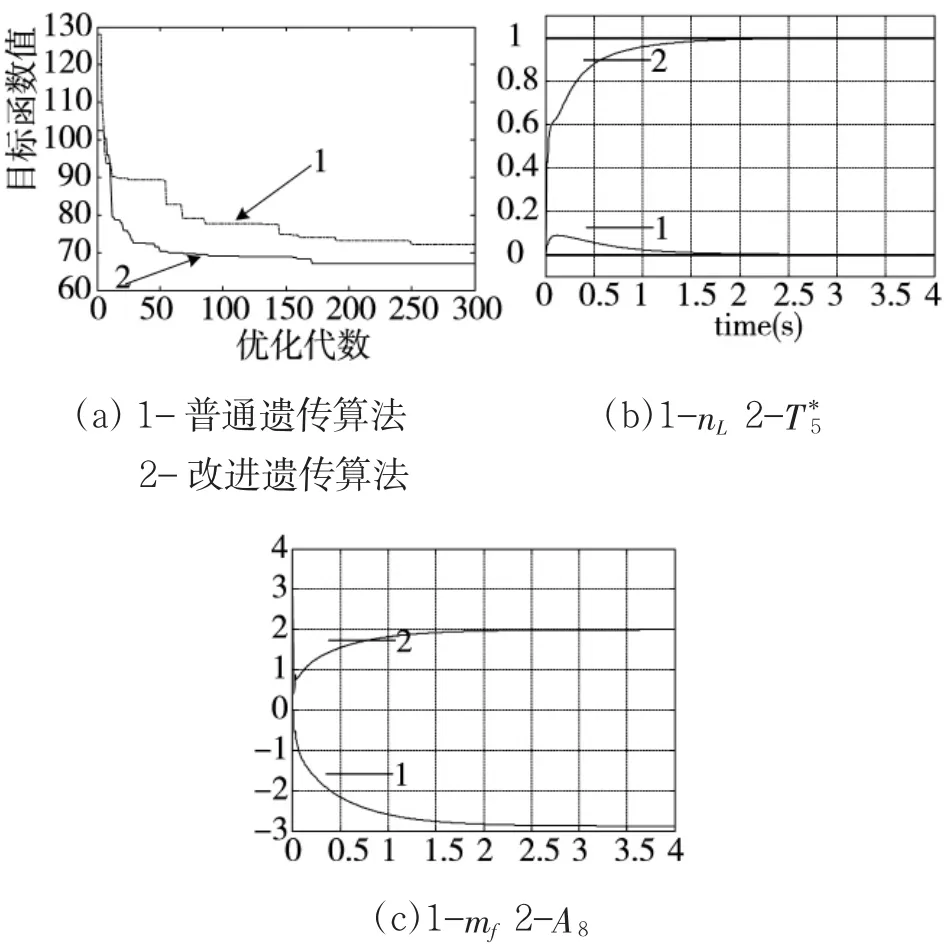
图4 H=0 km，Ma=0涡轮后总温为阶跃输入时的解耦仿真控制曲线

发动机状态空间模型的参数随着大范围飞行条件的变化而发生变化，发动机在 H=10 km，Ma=1.3状态下的仿真结果如图5、图6所示。由仿真所得结果可以看出，本文所设计的控制器在模型参数变化情况下仍能得到比较好的控制效果，在没有稳态误差的前提下，改善了发动机的动态特性，并且使系统仍能很好满足解耦的要求。

图5 H=10 km，Ma=1.3低压转子转速为阶跃输入时的解耦仿真控制曲线

图6 H=10 km，Ma=1.3涡轮后总温为阶跃输入时的解耦仿真控制曲线

4 结论

在具有网络短时延的航空推进分布式系统中，针对控制变量之间的耦合问题，提出了一种基于改进型遗传算法的发动机双变量PID解耦控制器的设计方法，该方法利用自适应遗传算法全局自适应寻优特性以及模拟退火算法的局部寻优特性，结合特殊目标函数的设计，对两回路控制器的PID参数进行寻优，从而实现了控制回路的解耦。通过对本章内容的研究，得到的主要结论如下：

①改进后遗传算法比普通遗传算法的寻优效率明显提高，并能够有效避免局部最小值，应用在航空发动机PID解耦控制器的设计当中，能够提高控制算法的实时性和控制精度。

②发动机通过同时调节供油量和尾喷管临界面积，可以使低压转速和涡轮后燃气温度跟随其给定水平，实现控制变量的解耦。

③对飞行包线内较大范围内的两个代表性工作点进行仿真，结果表明：本文所设计控制系统调节时间在1.5 s内，不存在超调量，2 s后即基本消除了稳态误差，控制量在可接受范围内，系统在拥有良好的动、稳态特性的基础上，很好地实现了变量间的解耦。

［1］杨华，郭迎清.基于RBF网络辨识的涡扇发动机双变量神经网络PID解耦控制［J］.航空动力学报，2007，22（8）：1391-1395.

［2］吴勇，谢寿生，唐奇，等.基于支持向量机的航空发动机PID解耦控制［J］.航空动力学报，2009，24（10）：2349-2355.

［3］李秋红，孙健国，周继超.航空发动机PID控制参数优化的改进遗传算法［J］.南京航空航天大学学报，2006，38（2）：162-165.

［4］孙健国.面向21世纪航空动力控制展望［J］.航空动力学报，2001，16（2）：97-102.

［5］KRISHNAKNMAR.Solvinglarge parameters optimization problems using genetic algorithms［R］.AIAA-95-3223-CP，1995.

［6］LI S L，SUN J G.Application of genetic algorithm to solving nonlinear model of aeroengine［J］.Chinese Journal of Aeronautics，2003，16（2）：69-72.

［7］王小平，曹立明.遗传算法-理论、应用与软件实现［M］.西安：西安交通大学出版社，2002.

［8］孙健国.基于遗传算法的航空发动机多目标优化PID控制［J］.航空动力学报，2008，23（1）：174-178.

Research on Decoupling Method for Distribute Control of Aero-engine

DUAN Jin-feng1，PENG Jing-bo1，XIE Shou-sheng1，WANG Li-guo2
（1.School of Aeronautics and Astronautics Engineering，Air Force Engineering University，Xi’an 710038，China；2.Unit 95507 of PLA，Guiyang 550000，China）

Aero-engine control system is quite a complicated multivariable system with its variables coupling each other which will impact on the static and dynamic performance of system and even will give rise to the phenomena of exceeding temperature or rev in its ultimate state which not only threats the flight safety severely but also restrict the advance of Aero-engine’s performance.To solve this problem，a PID decoupling controller based on improved genetic algorithm is presented.The digital simulation of the control system has proved its excellent performance in controlling precision and tracking.The method is suitable for the aero-engine control system since it can assure satisfactory transient performance of aero-engine in condition of different environment and alleviate the coupling influence of each control variable effectively.

Aero-engine，Distributed control，Simulated annealing，Adaptive genetic algorithm，Decoupling

V239

A

1002-0640（2017）05-0037-05

2016-03-18

2016-05-09

国家自然科学基金（51476187，51506221）；陕西省自然科学基础研究计划青年人才基金资助项目（2015JQ5179）

段进峰（1993- ），男，山东聊城人，硕士研究生。研究方向：航空发动机推进系统综合控制与故障诊断。