建立模型思想,提升数学素养
2017-06-18黄肖慧
黄肖慧
摘 要:“模型思想”是数学的基本思想,更是数学学科的核心素养,贯穿于小学数学教学体系之中。基于“核心素养”本位的数学课堂,在综合与实践活动中融入数学建模教学,培养学生的模型思想,教师可以做出哪些努力?将从创设问题、建立模型、求解验证三个方面对实施策略展开阐述。
关键词:数学素养;综合与实践;数学建模;模型思想
“模型思想”是数学的基本思想,更是数学学科的核心素养,贯穿于小学数学教学体系中。新课标四大教学领域之一的“综合与实践”,是培养学生的模型思想、应用意识和创新意识的良好载体。基于“核心素养”本位的数学课堂,在综合与实践活动中融入数学建模教学,培养模型思想,我们可以做出哪些努力,给学生带来什么样的改变?笔者就此展开了研究与思考。
一、创设问题——常备“数学”的眼光
“综合与实践”教学与模型思想的建立均以问题为载体,两者在问题的设计上有着异曲同工之处,教师在问题情境的创设中应具备“数学”的眼光。以渗透模型思想、提升数学素养为目标,选取的问题应体现以下特点:
1.趣味性
兴趣是由好奇心所产生的精神向往,是实践与探索的前提。因此,活动中所选择的问题要具有一定的吸引力。而且,问题情境中的信息应容易获取,建模所需的数学知识相对简单,学生通过努力能够顺利建模,为建立成功、自信的学习体验作好铺垫。
2.实践性
选取密切联系学生的生活经验的问题情境,更能牵动探索与思考的热情。来源于自然、社会、生活、其他学科和数学内部,学生有相关经历、能够实践的活动,都是不错的选择。
3.新颖性
最好选取学生第一次遇到的新问题,有别于常规的实际问题,为学生提供深入探索和创造的机会,在建模过程中发展思维、提升能力。
4.开放性
问题要具有一定的开放性。从条件、解决问题的过程到结论都具有开放性,体现解决问题思路和方法的多样化。通过交流与总结,触发不同层次的思考和创造性,感知同一问题建模方法与结果的多样性,形成从多种角度出发探讨问题的学习方式。
例如,人教版四年级《1亿有多大》。对照上述四个特征,问题的现实模型学生比较熟悉,获取建模信息不难,可通过同伴研讨、教师指引获得;建模时主要用到简单的测量、乘法、单位换算与数的大小比较等基本数学知识,相对简单;“1亿有多大”有别于常规的大小比较问题,是学生第一次遇到的新问题;解决方法和结论都不唯一。有质量的问题可以成为支点,撬动学生的探究欲望和思辨能力,使数学综合素养得到充分发展。在创设问题这一环节,教师能常备一双“数学”的眼光显得弥足珍贵。除了教材中提出的问题,教师要注意收集、开发研究专题,并鼓励学生捕捉身边的数学信息,自己发现和提出问题。
二、建立模型——培养“数学”的思维
用数学的思维分析世界,用数学的语言表达现实世界,是建立数学模型的重要方法。养成“数学”的思维,学生才能在获取信息之后正确、有序地形成解决问题的思路,建构数学模型,使综合与实践活动得以顺利开展。
1.用数学的思维分析世界:培养符号意识,渗透函数思想
在研究中我们发现,数学学科各项核心素养之间是相辅相成、密切相关的,在引导学生建立模型思想的同时,符号意识和函数思想的建立其实发挥着不可忽视的重要作用。在数学建模过程中,恰当地引导学生用函数建构模型,用符号语言表达模型,既是建模的需要,也是综合与实践教学的要求。因此,把培养符号意识、渗透函数思想与数学建模相结合,让学生用数学的思维参与“综合与实践”活动,是提升数学素养的有效策略。
2.用数学的语言表达现实世界:培养语言表达能力,应用几何直观
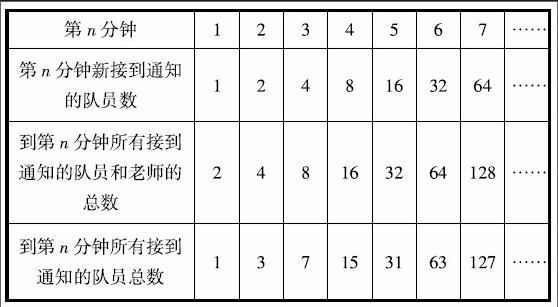
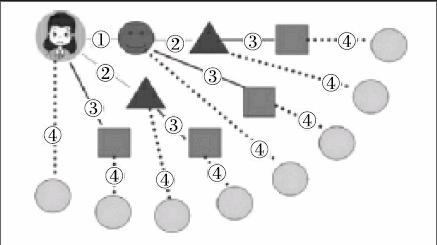
根据小学生的思维特点,基于数学建模的综合与实践教学应当充分运用几何直观,并重视交流过程中学生语言表达能力的培养,用数学的语言表达现实世界。例如,五年级下册《打电话》,通过创设学生熟悉的“打电话”情境,研究“怎样花最少的时间通知到15位队员”这个问题,建立解决问题的模型,体会策略的多样化和优化,感受数学的价值。在“每个人都不空闲”的方向引领下,几何直观图的应用帮学生找到了最优方案:
从图中学生能清楚地发现隐含的规律,并能用自己的语言说明:每一分鐘所有接到通知的队员和老师的总数是前1分钟所有接到通知的队员和老师总数的2倍;每增加1分钟,新接到通知的队员数正好是前面所有接到通知的队员和老师的总数。学生的语言描述表明他们通过看图寻找出规律和算法,而不是根据数列规律推理,由此可知,几何直观和语言描述在数学建模中的作用举足轻重。
列表是另一种表征思维过程的数学形式,更简洁明了,有利于培养学生的符号意识及思维的有序性、全面性。通过观察表中数据,学生能够发现:到第n分钟所有接到通知的队员和老师的总数是一个等比数列,就是,到第n分钟所有接到通知的队员总数就是人数。数学模型的符号化提炼,使函数思想得到有效渗透,对于学有余力的学生来说,是进一步体会推理、优化、模型等数学思想,培养抽象思维能力不可或缺的时机。
“综合与实践”本质上是一种解决问题的活动,我们希望帮助学生积累数学活动经验,培养“数学”的思维;在建立模型的过程中积累数学智慧,提升数学素养。
三、求解验证——品味“数学”的魅力
数学的魅力是什么?数学源于生活,但并不等于生活本身,它是对生活中的数量关系与空间形式的提炼;数学不仅仅是计算,在运用数学进行思维的过程中,所锻炼的不仅是思维方法,更重要的是观念的改变。笔者以为,这些在基于数学建模的综合实践课上有较好的体现。
从某种意义上来讲,模型思想就是将一个问题的解决,拓展为一类问题的解决。正如荷兰数学家弗赖登塔尔所说:“数学来源于现实,也必须扎根于现实,并且应用于现实。”当学生建立数学模型以后,教师应该引导学生应用模型解决问题,使数学模型成为沟通实际问题与数学知识的桥梁,从而帮助学生提升数学模型的应用水平,积累模型经验,形成初步的模型思想。运用数学模型解答实际问题,不但使学生充分体会到数学模型的实际应用价值,而且进一步培养了他们应用数学的意识和综合应用数学解决问题的能力。这些活动的开展,将对学生数学素养的形成产生不可估量的推动作用,这也是“综合与实践”课的内涵及教育价值所在。
“综合与实践应用”是充满实践、探索、碰撞的过程,是学生亲自参与、生动的过程。综合实践应用与模型思想相结合,是学生形成深度学习和探索能力的重要途径。基于数学建模的“综合与实践”教学,需要教师坚持不懈、循序渐进的渗透、反思、领悟,使学生对模型思想的认识、对数学的理解从“量的积累”达到“质的飞跃”,唤醒数学意识,提升数学素养。
参考文献:
[1]张丹.小学数学教学策略[M].北京:北京师范大学出版社,2010.
[2]曹培英.“数学课程标准”核心词的实践解读之八-模型思想(下)[J].小学数学教师,2015(2):4-11.
