一题多解 培养学生求解能力

云南省普洱市第一中学(665100)

王爱华●

一题多解 培养学生求解能力

云南省普洱市第一中学(665100)

王爱华●

在复习课的教学中，时间短、任务重，要在较短的时间内完成全面复习工作，对学生来说是一件不易的事.教师应当在有限的时间内讲求方法、精选例题，在加强基础知识复习巩固的同时，注意典型例题、相关知识的分析和讲解，以点带面，触类旁通，一题多解，培养学生多角度分析思考问题的思维，启发诱导学生，灵活应用所学知识解决问题的能力，从而事半功倍.也不失中学数学教学的需要.本文仅借在解不等式复习中的一例说明之.

示例 解不等式|lg(1-x)|>|lg(1+x)|.

本题是一道综合的含绝对值符号的不等式，关键是先去掉绝对值符号.分析讲解前，先由学生独立思考，组织讨论，提出各自的解法，然后列出解法的主要步骤，直至化为等价的不含绝对值的不等式(组).详解可由学生下去完成.

角度一：(居于绝对值不等式的结构，可考虑变形为形如：|f(x)|>a或|f(x)|0)的不等式去绝对值符号)

∵x≠0(若不然有lg(1-x)=lg(1+x)=0)

∴1+x≠1，即lg(1+x)≠0得|lg(1+x)|>0

点评 由以上变形，问题转化为一般对数不等式进行讨论解之.对数函数的性质也从中得到复习和巩固.

角度二：(由于平方可去掉绝对值符号，所以可考虑用两边平方的办法来处理绝对值符号，但要注意满足两边平方的不等式性质).

∵a2>b2⟺|a|2>|b|2⟺|a|>|b|(a,b∈R)

∴|lg(1-x)|>|lg(1+x)|

⟹|lg(1-x)|2>|lg(1+x)|2

⟹lg2(1-x)>lg2(1+x)

⟹lg2(1-x)-lg2(1+x)>0

⟹[lg(1-x)+lg(1+x)][lg(1-x)-lg(1+x)]>0

点评 通过去绝对值符号、问题转化为二次型不等式，对对数的运算、实数的符号法则及对数函数的性质从中得到复习.进而化为分式不等式(组)及二次不等式(组)求解，相应不等式的解法得以复习.此法思路明朗便于理解.

角度三：(由于原不等式含有对数函数形式，可由其定义域、值域出发，分析x的取值范围，讨论区间去绝对值符号).

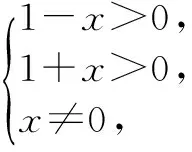
点评 通过区间讨论去掉绝对值符号，问题转化为简单的分式不等式组求解.此法技高一筹，迅速快捷.同时培养了学生利用讨论命题成立的条件来化繁为简的解题思想方法.

角度四：(去绝对值符号，还可考虑绝对值的定义，讨论去绝对值符号).

运用绝对值定义，直接化为以之等价的不等式组：

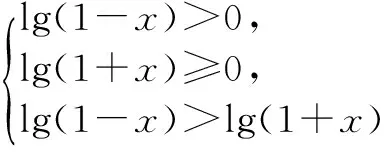
点评 此法充分运用基础知识，使问题转化为对数不等式组，进而转化为分式不等式组求解，但较繁.

角度五：(由于原式两端含有绝对值符号，且非负，可考虑直接将一端视为|f(x)|0)型中的a，逐次去绝对值符号).

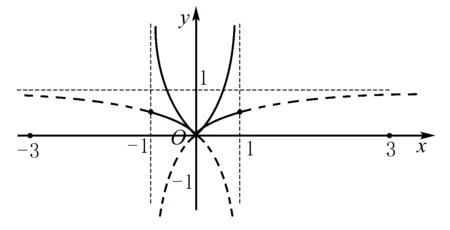
由|lg(1-x)|>|lg(1+x)|⟹-|lg(1-x)|

点评 逐次去掉绝对值符号后，问题转化为对数不等式组及分式不等式组求解，仍较繁！

角度六：(由于函数y=|lg(1-x)|及y=|lg(1+x)|的特征图形不难作出，故可考虑数形结合，作图求解).

由图形立即可看出，原不等式的解为0

点评 用此法解起来不仅直观、快捷.通过作图可明确有关函数的定义域、值域、性质，还可复习带绝对值的函数图象、分段函数的图象及平移等知识，培养数形结合的解题思想.

思考题：

(1)解不等式|log2(1-x)|>|log2(1+x)|.

(2)指出上述不等式与不等式|loga(1-x)|>|loga(1+x)|(a>0,a≠1)是否同解？为什么？

(3)证明不等式|loga(1-x)|>|loga(1+x)|(a>0,a≠1)成立的充要条件是x∈(0,1).

由以上分析不难发现，本例的求解不仅对考纲要求的多个知识点得以复习巩固，而且对培养学生知识迁移和基本的数学方法、观察、分析、归纳、综合、类比、抽象、概括等数学思维，以及函数与方程的思想、数形结合的思想、逻辑划分的思想、化归与转化的思想等方面，都起到良好的启发诱导作用，从而更有效地利用有限的时间指导学生复习，提高复习效率.

G632

B

1008-0333(2017)01-0055-02