巧用变式 领悟规律——含有两个变量的函数的任意性和存在性问题

张晓艺●

巧用变式 领悟规律
——含有两个变量的函数的任意性和存在性问题

河南省信阳高级中学高三文科(1)班(464000)

张晓艺●

在各种资料，在考试甚至高考中，经常出现两个变量的函数问题，这类问题课本上并没有出现过，但它的知识源于课本中涉及到的两集合间的关系，及函数最值，既能考查学生基础知识的掌握又能考查学生分析问题解决问题的能力，源于课本，高于课本，故这类问题备受命题者青睐.以前笔者在学习中是用遇到一个，记录一个的方法处理的，当时也能搞明白，但过后再考，仍然做不对，出错率极高，在最近我市的一次考试中，又设计了这样一道选择题，题目如下：

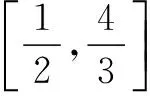
考后通过阅卷分析发现，即使是很优秀的学生，这道题也出错，问卷调查后发现错因有两个：

(1)不会分析问题，无法把该问题转化为两段函数值域之间的关系，反映出能力不足；

(2)即使分析出要求两段函数值域，但求解f(x)的值域时出错，反映出基础不牢.针对这种情况同学们是这样处理的：

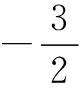
但我的探索却没有停止，为了认清这类问题的本质，学会分析，在此题的基础上又设计了以下三道变式：

在上面例1的基础上，我和同学们对上述变式展开讨论，得出的结论如下：

f(x)g(x)f(x)=g(x)需具备的条件(设f(x)的值域为集合M,g(x)值域为集合N)∀∀M=N∀∃M⊆N∃∀N⊆M∃∃M∩N≠∅

下面对例1再做一组变式，以便更深刻地理解这类问题.

在借鉴变式四的分析思路的基础上，学生类比概括出以下规律：

f(x)g(x)f(x)≤g(x)需具备的条件∀∀f(x)max≤g(x)min∀∃f(x)max≤g(x)max∃∀f(x)min≤g(x)min∃∃f(x)min≤g(x)max

通过以上8个问题的专题讲解，学生对含有两个变量的函数的任意性，存在性问题的求解思路清晰明了，在后来各类考试中再出现这类问题都能准确求解.

下面提供两道综合题，再次体会上述规律的应用.

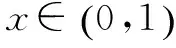
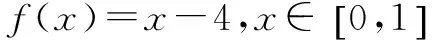
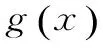
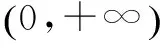
G632

B

1008-0333(2017)01-0050-02