追根溯源探解法变式推广觅思路——一道模拟题的解法及启示

杨 虎●

追根溯源探解法变式推广觅思路
——一道模拟题的解法及启示

甘肃省礼县职业中等专业学校(742200)

杨 虎●

三角函数这一部分的知识在高中数学教学中占有极其重要的地位，高考中更是考查的热点.在指导学生学习时，一道三角函数的证明题引起笔者的学习兴趣，追根究底对其源头、解法进行了探究，并对其变式进行思考、推广，来寻觅这一类问题的解题思路.

一、题目展现及题源探究

这是一道以三角函数为背景的证明题.其等式左边的分子与分母是角α，3α与5α的正、余弦的和，右边是3a角的正切值，形式优美，和谐简洁.追根究底，在进一步学习时笔者发现，1986年的一道高考(文科)数学题与此题极为相似.

将近三十年的一道陈题，又变换了形式出现在学生的模拟题中，体现了数学考试还是万变不离其宗，也可以看成是问题1的题源，其证法也很多.下面笔者以问题1为例进行探索，并对后续教学进行反思.

二、解法探索

探索一：顺水推舟 自然得证

证明题最自然的解法也就是从左往右证(或从右往左证)——顺水推舟，即把等式左边经过化简、变形而得到右边的式子，考虑到右边是3α角的正切值，所以左边在化简时应保留3α角，将α角与5α角进行组合、变形，产生3α角，向右边靠拢，自然得证.需要说明的是，等式左边应用和差化积时，必须是一次同名三角函数方可实行.若是异名，必须用诱导公式化为同名.

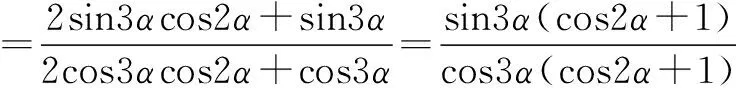
探索二：层层递进 分析证法

探索三：无中生有 添加项法

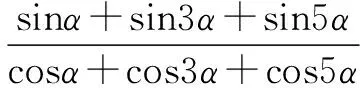
探索四：正难则反 归谬得证

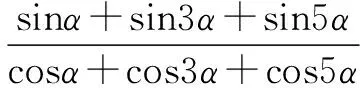
探索五：巧设参数 等比助力

三、变式探究

在以上的探索中不难体会到，这一类问题证法多样，但其基本的思路或者说最有效的方法还是从右到左——自然得证与分析证法.下面利用自然证法证明此变式题.

四、三个推广

基于以上的解法探索与变式探究，进行如下的三个推广：

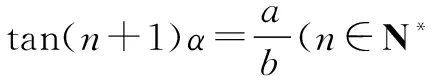
五、两点教学启示

启示1：在教学与学生学习过程中尝试一题多解.

一题多解可以理解为从不同的角度对一道习题进行解答，在教学过程中与学生学习过程中实施一题多解，首先有利于调动学生学习的积极性.通过教师的引导，学生可能会对一道题给出不同的解法，让课堂成为学生探究、交流的场所，让课堂不仅有预设更有生成，突出了以学生为主体的课标理念，提高了学生的学习兴趣.其次有利于培养学生的创新思维，锻炼思维的灵活性.在寻求问题的解法中，学生通过对比、探索，能够发现更简捷、更有效的解题方法，拓展了学生的创新思维.再次有利于学生积累解题经验，丰富解题方法，从而达到提高解题能力的目的.

启示2：在教学与学生学习过程中尝试变式及推广.

如何让课堂成为高效的课堂是中学数学教学研究和改革的重要课题，而应试教育不可避免地带来了教学中的“题海战术”，这无疑加大了学生学习的负担，甚至让学生厌学.那么在教学中引导学生对一个知识点、对一道习题，不仅从多角度去探索，更要研究其可能的变式，举一反三并加以推广，触类旁通，深入挖掘知识点、习题中蕴含的变式创新因素，培养学生的求异思维，创新能力，提高应变能力让课堂教学成为真正的高效课堂.

G632

B

1008-0333(2017)01-0012-02