运用直觉思维，妙解数学问题

江苏省江阴中等专业学校(214400)

崔永红●

运用直觉思维，妙解数学问题

江苏省江阴中等专业学校(214400)

崔永红●

直觉思维是逻辑思维中最活跃、最积极、最具有创造性的成份，直觉思维为逻辑思维提供了动力并指示着方向，逻辑思维则对直觉思维作出检验与反馈，是直觉思维的深入和精化.直觉思维在数学解题中具有重要的作用.

直觉；导向；选择；创造；判断

直觉思维是指不受固定的逻辑规则约束，直接领悟事物本质的一种思维方式.直觉思维作出的结论并不是主观臆断，而是以扎实的知识为基础，以对事物敏锐的观察、深刻的理解为前提，从而对研究的问题提出合理的猜测和假设，直觉思维往往表现为突然的认识和领悟.直觉思维主要表现在思维对象的整体性，思维产生的突发性，思维过程的非逻辑性，思维结果的创造性和超前性以及思维模式的灵活性和敏捷性等.

直觉思维相对于逻辑思维，最重要的特征是在没有经过严格的逻辑推理之前，迅速对事物作出判断、得出结论，而这种结论还需要严格的逻辑证明.直觉思维在数学解题中具有重要作用.

一、运用直觉思维，为解题提供导向功能

在数学解题中，通过细心观察，从平常的现象中发现不平常的东西，从表面上无关的东西中发现相似点或因果关系，为实施解题提供导向、思路和途径.

若使用直接求法，需先作如下变形：

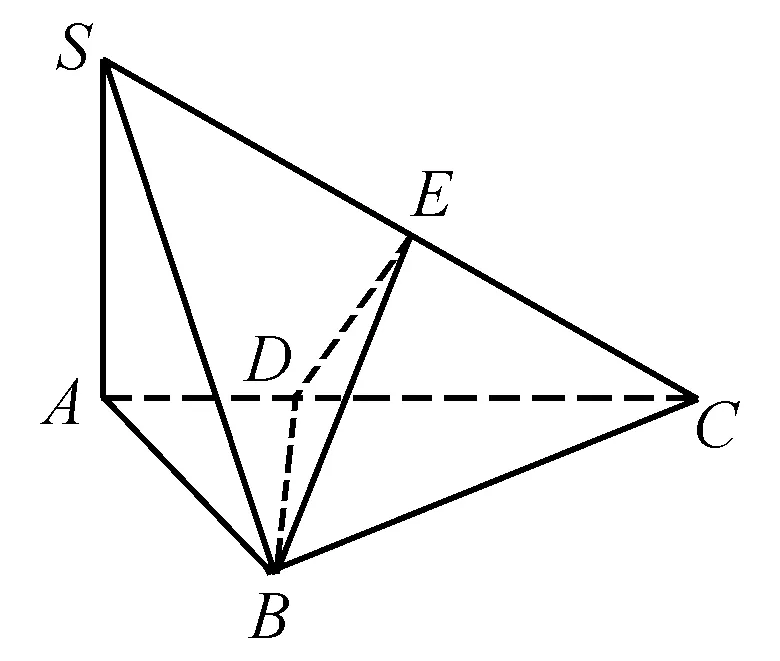
案例二 如图，在三棱锥S-ABC中，SA⊥面ABC，AB⊥BC，DE垂直平分SC，SA=AB，SB=BC，求二面角C-BD-E的大小.

本题的关键是确定二面角的平面角，通过认真观察，分析条件，依靠直觉思维，得出∠EDC是所求的二面角的平面角.这里的直觉思维也不是凭空想象，而是由题目的已知条件，从整体上把握而产生的猜想，是观察题目所给的图形，由直观而产生的直觉.这种直觉思维的产生往往在不言中，有时也可能思维受阻，在不知所措的情况下突然来了灵感，一下子就意识到∠EDC就是所求的二面角的平面角，正是由于直觉思维的先导作用，才为证明和计算铺平了道路.

二、运用直觉思维，为解题提供选择功能

在数学选择题中，由于它有备选项，有相当大的提示性，给试题的解答提供了丰富的有用信息.通过直觉感知、直觉思维选择不同的逻辑材料或逻辑通道，为解题活动展现了广阔的天地，大大增加了解答的途径和方法，常常潜藏着极其巧妙的解法.在这一过程中，直觉思维具有不可替代的作用.

A．1 B．2 C．3 D．4

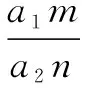
本题采用直接法，需计算不等式组：

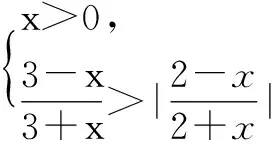
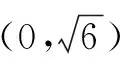
本题是培养学生直觉思维的好素材.解选择题时学生使用猜的方法在一部分老师中还存在着不同的认识，他们总认为数学就是严格的推理、严密的证明，其实猜是直觉思维的特性，是发明创造的基础，是人的素质的标志，我们不鼓励胡猜、乱猜、瞎猜，而是倡导合乎情理的猜想.

三、运用直觉思维，为解题提供创造功能

在数学活动中，往往不存在一种凝固不变的思维通道去引导我们按图索骥地解决各种问题.因此对某些数学问题，若能由它的条件和结论，联想起与之类似的问题、类似的形式、类似的解法，或者联想相关的定理、性质和图形，常能诱发直觉，促使问题得到解决.

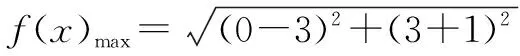
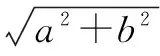
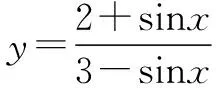
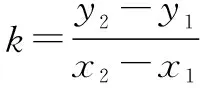
四、运用直觉思维，为解题提供判断功能

有一些数学问题，往往需要先依靠直觉作大致的估算与猜测，而不是先动手计算或认证，有时单靠逻辑推理无法达到快速解决问题的目的.缺乏直觉思维能力，就只能按部就班地逻辑推理，而富有直觉力的人，则能凭直觉迅速作出正确的解答.

案例七 用1、2、3、4、5这五个数字可以组成很多五位数，这些五位数中素数的个数是____.

A．68 B．27 C．0 D．133

许多同学的做法是先排除个位数是2、4、5的情况，再逐一考查剩下的48种情形，用筛选法去解决问题.但有直觉思维习惯的同学，会从整体上把3、2、5、4、1五个数字考查一番，由3+2+5+4+1=15，便一眼看出不论怎么改变数字的位置，排出的五位数一定是3的倍数，不是素数，因此选C.

案例八 若(z-x)2-4(x-y)(y-z)=0，则x,y,z成等差数列.

我们可以先把已知条件左边的式子展开，然后分解因式而得证.如果我们细心分析已知条件的外形，就可以联想到一元二次方程有等根的条件Δ=b2-4ac=0.

因此，构造一元二次方程(x-y)u2+(z-x)u+(y-z)=0

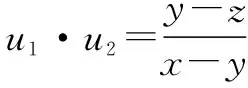
教师根据教学内容创设适宜的直观情境，诱发学生的直觉思维，促使学生主动发现新知，这不仅能激发学生的兴趣，而且能加深对新知识、新方法的理解和认识.当然，直觉思维得出的结论可能正确，也可能错误，需要运用逻辑推理或实践加以检验.因此在教学中，一方面要鼓励学生运用直觉思维对问题进行大胆猜想，另一方面又要培养学生对猜想的结论加以分析认证，克服直觉思维的片面性.

[1]王正梅.例谈数学直觉思维的培养[J].江苏教育研究，2011(33)

[2]袁庆国.浅谈学生数学直觉思维能力的培养[J].教育实践与研究，2009(04)

[3]高蕾.如何在数学教学中培养学生的直觉思维能力[J]，教育教学论坛，2011(02)

[4]刘云章.数学活动中的直觉与灵感[M].北京：中国大百科全书出版社，2006.2

G632

B

1008-0333(2017)01-0005-02