含参数不等式恒成立问题的求解技巧

江苏省淮阴中学高三(6)班(223000)

范 茗●

含参数不等式恒成立问题的求解技巧

江苏省淮阴中学高三(6)班(223000)

范 茗●

所谓含参数参不等式恒成立问题，主要是指在恒成立条件下，已知不等式解集求参数的取值范围问题，它涉及知识点多，覆盖范围广，思想方法深刻，技巧性、综合性以及灵活性强，是历年数学高考的热点和难点内容.不少同学在求解含参数不等式恒成立问题时，往往束手无策，难以找到突破口，对此，笔者总结了含参数不等式恒成立问题的几种求解技巧和方法，以供同学们参考借鉴.

一、参数分离，最值转化

参数分离，是求含参数不等式恒成立问题较为常用的方法之一，它是指在含有参数的不等式恒成立问题中，借助恒等变形，将所求参数(或其代数式)从不等式中分离出来，并置于不等式一端，从而将原问题转化函数最值或值域问题，简化解题过程，使问题快速有效获解.

例1 已知函数f(x)在R上是减函数，对一切x∈R不等式f(m2-2sinx)≤f(2m+1+cos2x)成立，求实数m的取值范围.

解 ∵函数f(x)在R上是减函数，由题设不等式知

m2-2sinx≥2m+1+cos2x对一切x∈R恒成立，

∴m2-2m-1≥cos2x+2sinx对一切x∈R恒成立，

设g(x)= cos2x+2sinx，∴m2-2m-1≥[g(x)]max.g(x)= cos2x+2sinx=-sin2x+2sinx+1=-(sinx-1)2+2,

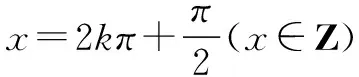
点评 对于某些含参数不等式恒成立问题，可将其中的参数分离出来，转化为求函数最大值或最小值问题.通常有:①f(x)g(a)(a为参数)恒成立⟺f(x)min>g(a).

二、分类讨论，严谨思维

分类讨论法，是数学解题中至关重要的思想方法.在解含参不等式恒成立问题时，若参数取值范围不同，或不等式左右两边的函数存在不确定因素时，可通过分类讨论的方法对参数进行求解，在分类讨论时应注意明确分类标准，做到不重复，不遗漏，从而提高解题的严谨性和准确性.

例2 设函数f(x)=x2+bx+c(b、c∈R).若对任意x1,x2∈[-1,1],有[f(x1)-f(x2)]≤4,求b的取值范围.

解 题设等价于f(x)在[-1,1]上的最大值和最小值之差M≤4，所以：

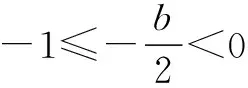
综上所述，可知b的取值范围是[-2,2].

点评 对于含参数不等式恒成立问题，倘若无法通过恒等变形分离参数，此时可以借助分类讨论的思想进行分析和求解.

三、数形结合，直观求解

数形结合法，直观形象.其特点是“见数想形，以形助数”，是求解含参不等式恒成立问题不可或缺的方法之一.在解某些含参不等式恒成立问题时，我们可以先将不等式两端的式子看成两个不同的函数，然后分别画出这两个函数的图象，接着观察函数图象特征和位置关系，最后列出有关参数的不等式，从而使问题迎刃而解.

点评 对于一些难以分离参数的不等式恒成立问题，可以利用数形结合思想，先作出符合已知条件的函数图象或图形，再利用函数图象的直观性，列出不等式，求出参数的取值范围.

总之，含参数不等式恒成立问题的求解方法灵活多样，不拘一格.在平时数学解题和学习中，同学们应注意多探索、多思考、多归纳、多总结，不断积累经验，掌握技巧和方法，从而提升自己的解题能力，有效突破解题障碍.

指导老师：陈 勇

G632

B

1008-0333(2017)01-0058-01