浅谈高中三角函数解题技巧

湖南省长沙市长郡中学(410000)

殷 雯 ●

浅谈高中三角函数解题技巧

湖南省长沙市长郡中学(410000)

殷 雯 ●

高中数学的学习，对于我们来说是非常重要的，三角函数是高中数学中必不可少的一部分，在数学知识的学习中，三角函数以各种形式出现在课本中.虽然三角函数的定义比较简单，但是其内容却包括了很多方面；通过正弦函数、正切函数、余弦函数的演变与运算，会不断丰富三角函数的学习内容.因此我们在解决三角函数问题时，解题技巧的掌握是十分重要的.本文概述三角函数的定义，分析几种常见的三角函数解题技巧，让同学们能够领悟知识点之间的连接关系，从而达到巩固知识和技能的目的，强化运算能力和学习数学的思维能力.

高中数学；三角函数；解题技巧

一、三角函数的定义与特点

从字面的理解上来说，三角函数即与角度有关的数学知识，高中学习的三角函数由简到难，最开始学习的是一些函数值，以角度为自变量，以正弦、正切、余弦函数为因变量的函数，其中都是关于简单的函数值变化值，例如：sin30°=1/2,sin90°=1，tan45°=1等简单函数值计算.高中数学知识的学习贯穿了三角函数，在简单的学习之后，会出现较难的恒等式，三倍角公式、积化和差、两角和、差公式等，这类运算需要学生熟练地掌握三角函数的公式，直接套用便能够解决问题.

图形的运用在三角函数中也是一大特色，每一个三角函数都可以利用图形表示出来，对于特殊的函数，也可以在图形上表示出具体的数值，而不常见的函数，也可以画出大概的图，将函数清晰地表示出来.但是，伴随学习难度的加大，知识的复杂化，双曲线函数的出现，将三角函数和解析几何、空间几何、复数等内容有效结合起来，成为了综合性的函数题目，多数同学都会有难以下笔的感觉.因此，高中三角函数的学习很简单也很难，我们必须要掌握基础知识，结合了解的解题技巧，才能够在解答时灵活自如地运用.

二、高中三角函数的解题技巧

1.角的转化

将题目中给出的条件角转变为单角，或者是将某一种角作为是基本的衡量标准，从而将其他的角转变为方便解题的角.

例1 求sin20°cos70°+sin10°sin50°的值.

解题思路 根据三角函数中的一些特殊角，结合相关公式，将一些角转变成为适合应用计算的特殊值，这样能够有效地简化计算的步骤，还能够让其中的某些项相互抵消，以此达到解题的目的.

解析 原式=1/2[sin ( 70°+20°)-sin( 70°-20°)]-1/2[cos(50°+10°)-cos(50°-10°)]=1/2(sin90°-sin50°)-1/2(cos60°- cos40°)=1/2 -1/2sin50°-1/4+1/2cos40°=1/4-1/2sin50°+1/2sin50°=1/4.

2.运用数形结合的方式

三角函数的学习与图形密切相关，从做过的习题中可以看出，除了一些运算简单、条件清楚明了，可以直接计算出来的题型以外，三角函数的题目都是与图形结合展开的，每一题三角函数都可以画出具有代表性的图形.因此，我们在学习的过程中，可以根据题目，直接画图，养成一个习惯；这样在做题的过程中，遇到比较复杂的题目便可以运用数形结合的方法解答.

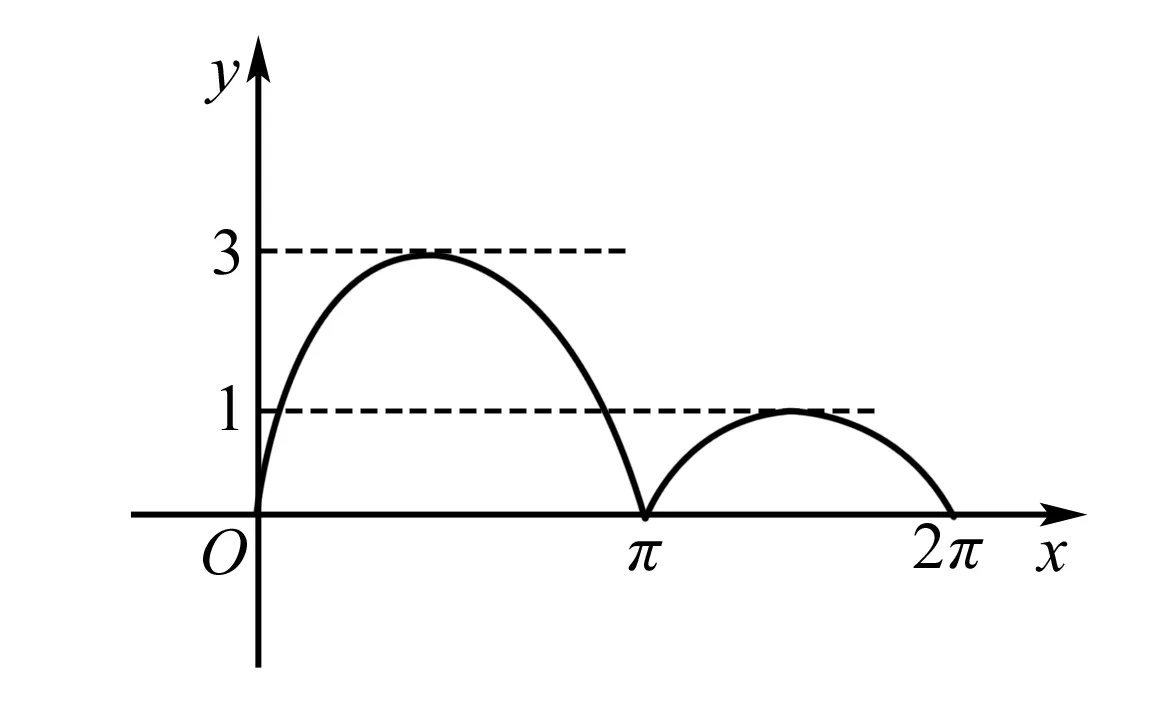
例2 函数f(x)=sinx+2|sinx|，x∈[0，2π]的图象与直线y=k恰有2个不同的交点，求k的取值范围.

解题思路 根据题目给出的函数解析式，可以对应地画出图象，可以从直观的图形中找出答案.数形结合的方法大大地缩减了解题的时间，提高我们的学习效率.

3.升幂降幂

升幂降幂公式是三角函数恒等式变形中常用的公式，升幂与降幂是相对应的公式.利用升幂降幂的公式或者逆向运用可以将三角函数的幂数改变，可以将三角函数简化，方便我们的解题过程.如下 2cos2α-1=1-2sin2α=cos2α、sin2α+cos2α=1 等公式，便是升幂降幂中常用的.

例3 化简 (1-cos4α-sin4α)/(1-cos6α-sin6α).

解题思路 将三角函数题型进行化简便是利用表达式将题目转化成更加简单的形式的一个过程，对其结果要求简单，因此其中涵盖的项数必须要做到最少，将高次幂全部化简，尽可能达到不存在，在分母中也要尽可能了转换掉复杂项，最后在能够求出数值的时候求出最终结果.

解析 升幂，逆用公式sin2α+cos2α=1.

原式=[(cos2α+sin2α)2-cos4α-sin4α]/[(cos2α+sin2α)3-cos6α-sin6α]=2cos2αsin2α/3cos2αsin2α(cos2α+sin2α)=2/3.

三角函数在解答过程中可以运用的解题方法多种多样.本文仅仅对其中几种方法进行了分析说明.三角函数囊括了函数的多种性质，以及对称性、周期性等，涵盖了丰富多彩的公式，能够在各种题型中转换.学习高中数学三角函数，掌握基础知识和解题步骤的非常重要的，但是对于解题技巧的掌握更是重点所在.只有这样才能够加强知识的连贯性，有效地提高我们的运算能力和思维能力.

[1]朱思文. 浅谈高中三角函数解题技巧[J]. 高中数理化, 2014(16):8-8.

[2]曹治. 浅析高中数学三角函数解析技巧[J]. 课程教育研究:新教师教学, 2015(20).

[3]赵飞. 浅谈三角函数变换技巧[J]. 高中数理化, 2016(2):13-13.

G632

B

1008-0333(2017)01-0047-01