构造长方体巧解立体几何题
2017-06-15江苏省东台中学高三
数理化解题研究 2017年1期
江苏省东台中学高三(9)班
张牧涵 指导老师 刘海东●
构造长方体巧解立体几何题
江苏省东台中学高三(9)班
张牧涵 指导老师 刘海东●
一、问题呈现
江苏凤凰教育出版社《普通高中课程标准实验教科书》必修二第40页思考:你能设计一个四个面都是直角三角形的四面体吗?
二、问题探究
1.解决这个问题的关键在于探求两个线面垂直,所以我采用了构造长方体来解决这个问题.
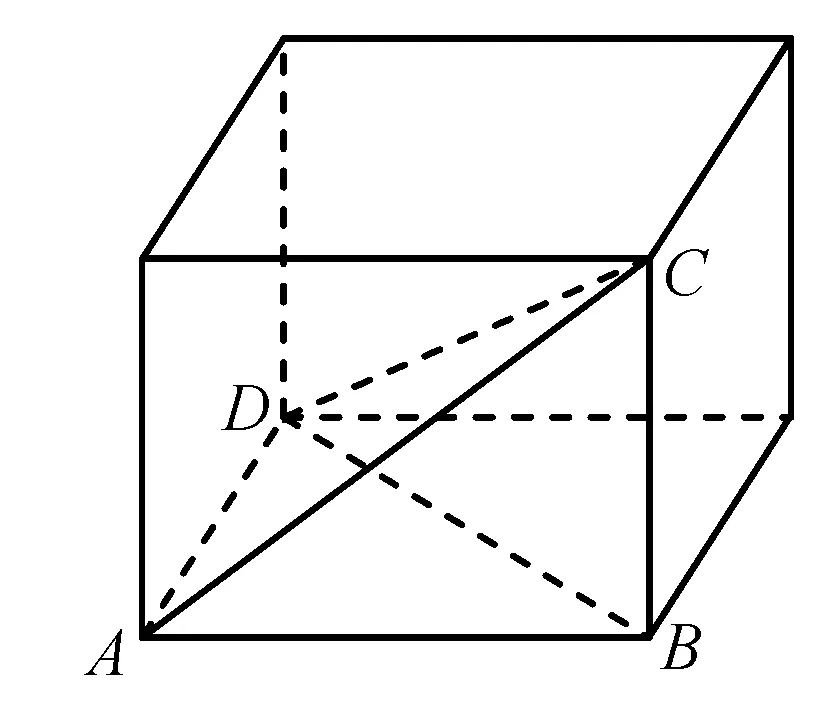
如图:长方体CD中,DA⊥平面ABC,则DA⊥AB,DA⊥AC,同理BC⊥平面ABD,则BC⊥AB,BC⊥BD,所以四面体ABCD中,四个面都是直角三角形.
2.联想到刚刚做过的一道习题.
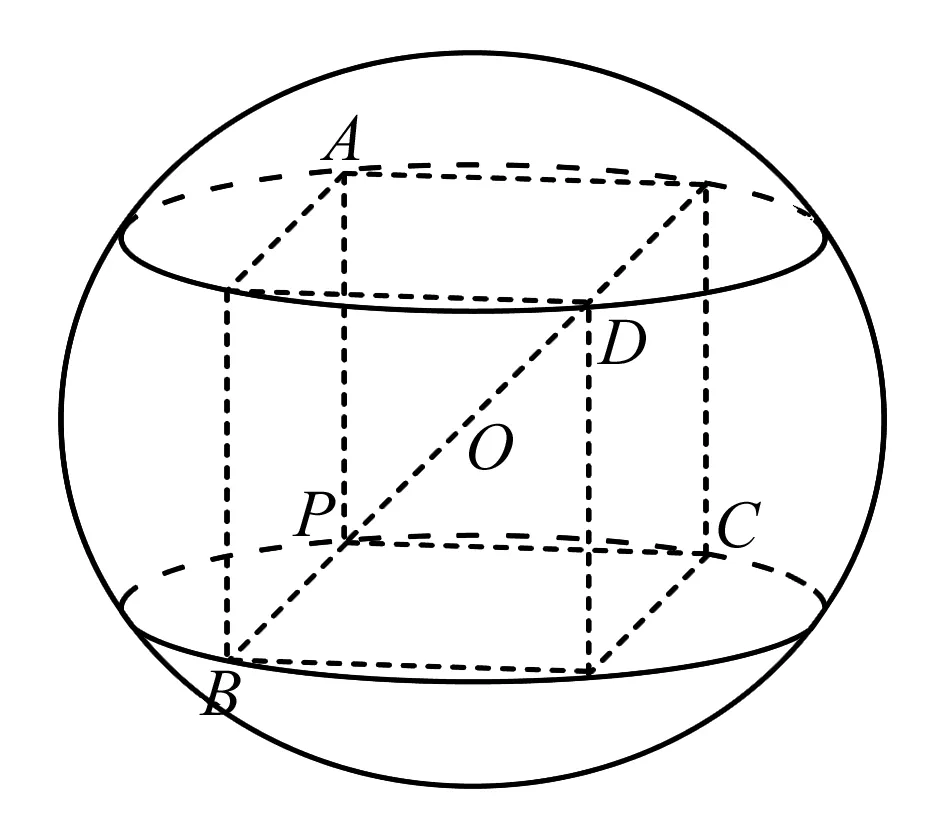
案例1 (必修二第71页第20题)设P、A、B、C是球O表面上的四个点,PA、PB、PC两两垂直,且PA=PB=PC=1 m,求球O的体积与表面积.
分析 此题由球的对称性知,以PA、PB、PC为棱可构造球的内接正方体PD,则有正方体的体对角线为球的直径.

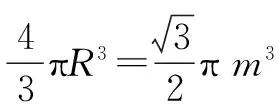
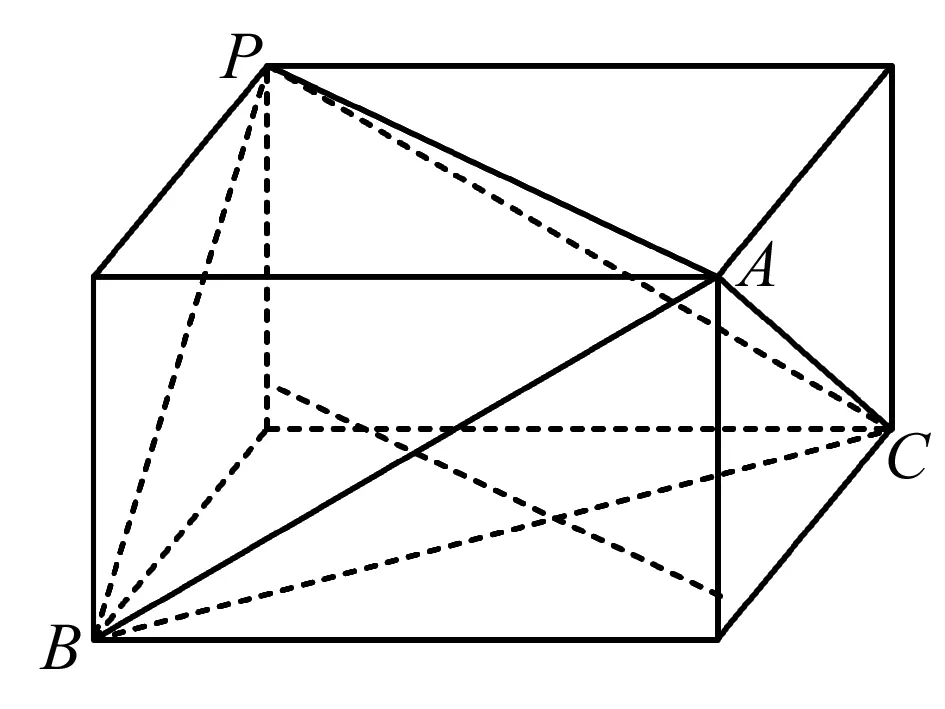




(老师点评:张牧涵同学创造性地使用已知条件和有关数学知识,构造长方体解题,关键在于挖掘已知条件,符合长方体的特征,以长方体为载体,在未知与已知之间架起一座桥梁.运用长方体的性质求解或转化为其他数学问题,能够提升学生的应用能力,增强创新意识.进一步发展学生几何直观和空间想象力,培养学生的直观想象的核心素养.)
G632
B
1008-0333(2017)01-0036-01
