例谈“绝对值三角不等式”的解题功效

甘肃省兰州市兰化一中(730060)

梁宗明●

例谈“绝对值三角不等式”的解题功效

甘肃省兰州市兰化一中(730060)

梁宗明●

选修4-5中，介绍了定理：如果a,b都是实数，则|a+b|≤|a|+|b|.当且仅当ab≥0时，等号成立. 把定理1中的实数换成向量a,b，结论依旧成立,它的几何意义是三角形两边之和大于第三边，等号成立的条件是a,b同向.由于定理与三角形之间的这种联系，我们称其中的不等式为绝对值三角不等式.在处理具体问题时，仅靠该定理是远远不够的，多数情况要用它的推广结论：

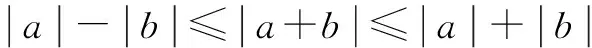
本文以历年高考题为例，说明其解题功效

一、解决存在性问题

1.(陕西文)若存在实数x使|x-a|+|x-1|≤3成立，则实数a的取值范围是____.

解析 只需(|x-a|+|x-1|)min≤3即可，利用结论2得：|a-1|=|(x-a)-(x-1)|≤|x-a|+|x-1|

由|a-1|≤3，解得-2≤a≤4.

2.(陕西理)若关于x的不等式|a|≥|x+1|+|x-2|存在实数解，则实数a的取值范围是 ．

解析 只需(|x+1|+|x-2|)min≤|a|即可，利用结论得：3=|(x+1)-(x-2)|≤|x+1|+|x-2|.

由|a|≥3，解得a∈(-,-3]∪[3,+).

二、解决恒成立问题

解析 只需(|x+3|-|x-1|)max≤a2-3a即可，利用结论得：|x+3|-|x-1|≤|(x+3)-(x-1)|=4.

由a2-3a≥4，解得a∈(-,-1]∪]4,+).

2.(陕西文)若不等式|x+1|+|x-2|≥a对任意x∈R恒成立，则a的取值范围是 ．

解析 只需(|x+1|+|x-2|)min≥a即可，利用结论得：|x+1|+|x-2|≥|(x+1)-(x-2)|=3.

故得a≤3.

三、解决证明问题

解析 由题知要证-3≤f(x)≤3，只需证明|f(x)|≤3即可.

而|f(x)|=||x-2|-|x-5||≤|(x-2)-(x-5)|=3，所以-3≤f(x)≤3.

解析 由要证明的结论可知，应该通过配凑相减消去变量x.

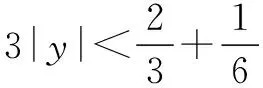
四、解决最值问题

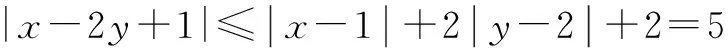
五、解决方程根的问题

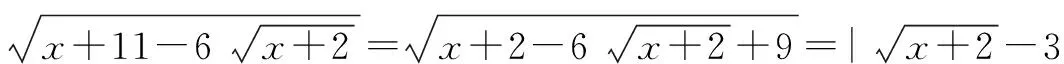
2. 求方程|5x+7|+|18-5x|=25的实根个数.

解析 因为|5x+7|+|18-5x|≥|(5x+7)+(18-5x)|=25，由结论1，右边“=”成立的条件得：

六、解决不等式问题

解不等式|2x+1|-|x-2|<|x+3|.

解析 原不等式等价于|2x+1|<|x-2|+|x+3|.又因为2x+1=(x-2)+(x+3),而|(x-2)+(x+3)|<|x-2|+|x+3|，即(x-2)(x+3)<0,所以原不等式解集为(-3,2).

G632

B

1008-0333(2017)01-0015-01