例谈解析几何中的设点和求点策略

福建省厦门松柏中学(361012)

卢云辉●

例谈解析几何中的设点和求点策略

福建省厦门松柏中学(361012)

卢云辉●

解析几何的解题教学与其说是教“解”法,不如说是教“想”法.帮学生提升策略水平,才是解题教学的根本之道.当两条曲线相交或相切时,必然关注它们的交点,对待交点存在设点与求点两种策略.下面就解析几何中的设点与求点两种策略作一些整理,便于读者参考与借鉴.

一、有关中点弦、弦长、两直线垂直等问题采用设点法

直线与圆锥曲线相交所得弦中点问题.这类问题一般有以下三种类型:(1)求中点弦所在直线方程问题;(2)求弦中点的轨迹问题;(3)求弦中点的坐标问题.其解法有代点相减法(点差法)、设而不求法、参数法和待定系数法等.

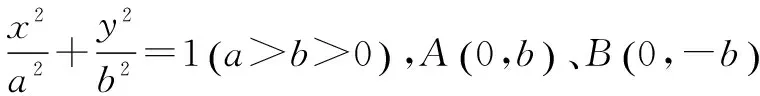
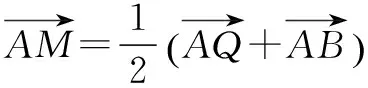
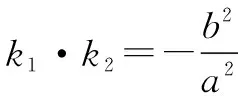
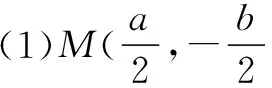
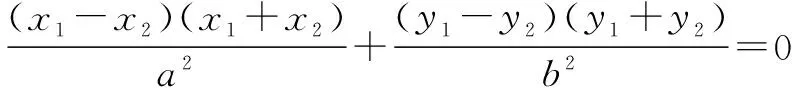
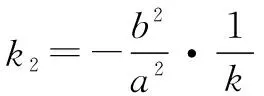
解决解析几何中有关弦长、两条直线互相垂直、对称、轨迹、定点等问题时采用设点法和韦达定理配合使用,能使问题化难为易,化繁为简,从而减少运算量.

(Ⅰ)求C1,C2的方程；

(Ⅱ)设C2与y轴的交点为M，过坐标原点O的直线l与C2相交于点A,B,直线MA,MB分别与C1相交与D,E.求证:MD⊥ME.

(Ⅱ)由题意知，直线l的斜率存在，设为k，则直线l的方程为y=kx.

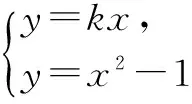
设A(x1,y1),B(x2,y2)，则x1,x2是上述方程的两个实根，于是x1+x2=k,x1x2=-1.

又点M的坐标为(0,-1)，所以

故MA⊥MB，即MD⊥ME.

点评 若联立直线l与曲线求出点D和点E坐标,再去计算kMD·kME的值,计算量较大.而采用设点及设直线就可以利用韦达定理中x1+x2,x1x2,y1+y2,y1y2的某些式子,从而简化计算过程,减少运算量.

二、问题中具有相同“结构”时采用求点法

数学解题中,接触到相同“结构”时,若能运用好“同理”思想,尤其在解析几何中就能回避繁琐的“雷同”运算.

设A(x1,y1),B(x2,y2)，则x1·x2=1.

故直线OA：y=k1x，直线OB：y=k2x，则k1·k2=-1.

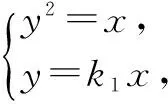
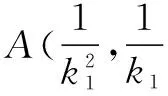
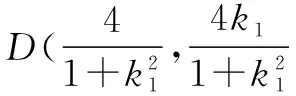
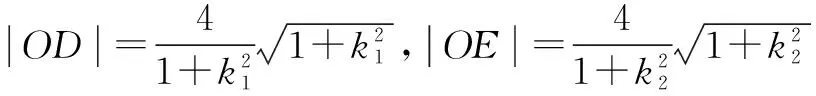
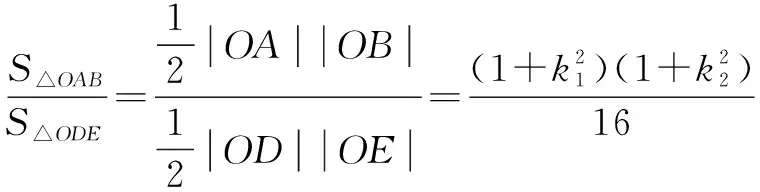
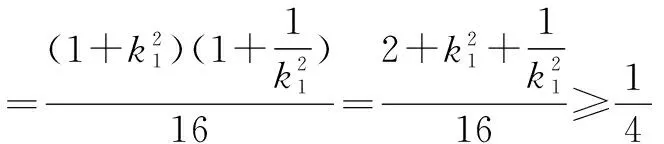
选C.

点评 由已知“过点(1,0)的直线与抛物线y2=x交于A,B两点”采用设点法推得射线OA⊥OB.下面围绕直线OA,OB展开分析与运算,求出A,D两点的坐标, 运用“同理”思想用k2替换k1,很快得到B,E两点的坐标.求出|OA|,|OD|的表达式,运用“同理”思想很快得到|OB|,|OE|的表达式,使问题获得解决.其中“同理”思想不仅回避了繁琐的“雷同”运算,而且简化了解题步骤,加快了解题速度.

总之,在处理解析几何问题时,若能选择性地使用设点法和求点法,不仅能回避繁琐运算,而且通过构建方程使问题得以巧妙化归,直奔结果.从而提高学生准确快速的解题能力.

G632

B

1008-0333(2017)01-0013-02