一道高考解几题的解析与探究

南京市大厂高级中学(210044)

雷亚庆●

一道高考解几题的解析与探究

南京市大厂高级中学(210044)

雷亚庆●

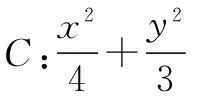
考题解析 如右图，设直线直线PA1﹑PA2斜率分别为k1﹑k2，设P(x0,y0).∵A1(-2,0),A2(2,0),

考题探究 自习研究本题，我们就会发现此题的实质是椭圆中的一类定值问题，我们把条件一般化就会得到下列一个结论

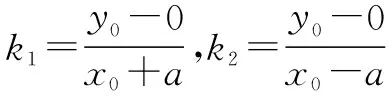
证明略.

继续用画板探究，我们就会发现更具一般性的结论.

证明 如图，AB为椭圆的一条中心弦，设直线PA﹑PB斜率分别为k1﹑k2，设P(x0,y0).

设A(x1,y1),则由椭圆对称性得B(-x1,-y1).

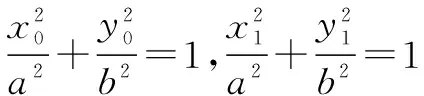
结论再推广 在学习圆锥曲线时，我们经常会把椭圆和双曲线加以类比，那么双曲线中有没有类似的结论呢？笔者用几何画板继续探究，发现类似结论在双曲线中仍然成立，不同的是定值不同而已，由此得到结论4.

证明与椭圆相类似，这里就不再证明了，事实上我们可以把上述结论概括为结论5.

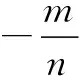
特别的：当m=n时，该二次曲线为圆，中心弦就是圆的一条直径，此时斜率之积为-1，此时两条直线互相垂直，这不就是我们初中学过的直径所对圆周角为直角的另一种表达吗？数学真是太奇妙了.只要我们做有心人，多思考，多探究，就一定会有让你惊喜的发现，数学的魅力也恰在于此.

G632

B

1008-0333(2017)01-0016-01