支持向量机模型在断层破碎带围岩变形预测中的应用

任庆国，苗兰弟

(陕西铁路工程职业技术学院，陕西渭南 714000)

支持向量机模型在断层破碎带围岩变形预测中的应用

任庆国，苗兰弟

(陕西铁路工程职业技术学院，陕西渭南 714000)

围岩变形预测是隧道安全评价及其指导后期施工的重要依据，为提高变形预测精度，结合工程实践，提出了PSO-SVM-BP预测模型的思路。首先，利用三次样条插值及二次平滑法对变形数据进行预处理，为后期变形预测奠定基础；其次，利用粒子群算法对支持向量机进行参数优化，建立PSO-SVM模型，并对围岩变形进行初步预测；最后，利用BP神经网络进行误差修正，达到综合预测的目的，并利用工程实例进行检验，以验证预测模型的有效性。结果表明：初步预测结果的相对误差均小于5%，而误差修正后的预测精度被提高到0.97%，预测精度较高，验证了预测模型的有效性，可为类似研究提供参考。

隧道工程；粒子群算法；支持向量机；BP神经网络；动态预测

随着中国经济建设的快速发展，交通运输事业取得了前所未有的进步，隧道建设规模也在不断地扩大。隧道属于地下工程，施工及运营环境复杂，其施工及后期运营安全在一定程度上依赖于监测工作[1]。隧道的变形监测数据可以用来有效地评价隧道支护结构及其围岩的稳定状态，也是信息化施工不可或缺的依据[2]。因此，对隧道变形监测数据的处理及预测，是判断隧道最终变形的基础，且通过建立相应的预测模型，使之能有效地预测隧道的变形趋势，对指导后期施工具有重要的意义[1]。

在隧道的变形预测中，支持向量机和BP神经网络是常用的预测方法。其中，支持向量机以结构风险最小化原理为基础，且依据凸二次优化问题，能有效地保证预测过程中的最优解[3]。但支持向量机模型在应用过程中，对使用者的经验依赖性较大，若使用者的参数设置不当，很容易导致预测结果陷入局部最优解，难以达到全局优化的目的，而粒子群算法具有很好的全局优化能力，能有效避免人为选择参数的不适性，提高预测模型的预测能力[4]。相关学者利用粒子群算法优化支持向量机的相关参数，建立PSO-SVM模型，将该模型应用到了隧道的变形预测中。例如：何延兵等[5]将该模型应用到具有蠕变性质的隧道位移变形预测中，显示预测结果与实际值的吻合度较高，为隧道的稳定性分析及事故处理提供了一定的理论依据；范思遐等[6]将该模型应用到隧道稳态及非稳态的变形数据预测中，结果验证该模型能有效地提高预测精度，具有较强的鲁棒性。同时，BP神经网络具有较强的非线性映射能力，对解决隧道变形的复杂非线性模拟具有明显的优势。例如：张志强等[7]将该模型应用到破碎带围岩的变形预测中，证明其具有较高的准确性和可靠性；龙浩等[8]则将其应用到隧道拱顶的变形预测中，预测结果科学可靠，有效地克服了开挖方式、地质条件等因素对预测结果的影响。上述研究虽已取得一定的成果，但研究过程的方法较为单一，缺乏系统性和完整性。为达到提高预测精度、满足工程需求的目的，本文拟将粒子群优化的支持向量机与BP神经网络结合，建立综合的预测模型，并根据监测数据的实时更新，实现变形数据的滚动预测，以期满足工程需要。

1 方法简介

1.1 基本思路

预测的总体思路是：利用三次样条插值及二次平滑法进行处理，实现对原始数据的预处理。随后利用粒子群算法对支持向量机进行参数优化，得到PSO-SVM预测模型，并采用该模型对隧道变形进行非线性预测。其次，再利用BP神经网络对前者的预测误差进行预测，建立误差修正模型，将两者的预测结果进行叠加即可获得隧道变形的高精度预测。同时，根据隧道监测过程中的数据更新，采用实时跟踪法，达到对隧道变形的实时滚动预测，其预测流程图如图1所示[9]。

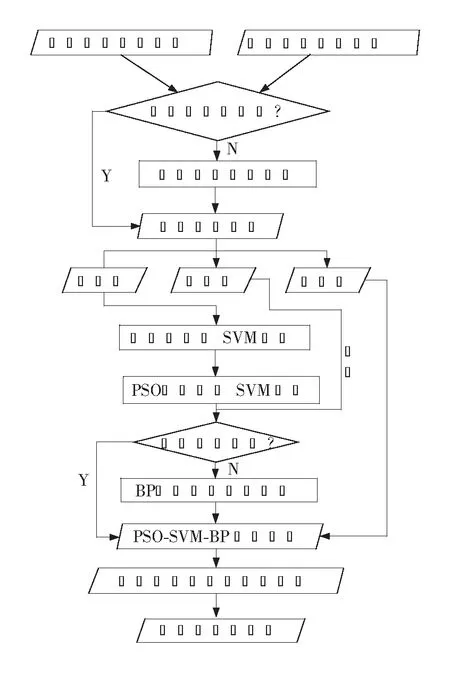
图1 优化PSO-SVM-BP预测模型流程图Fig.1 Flow chart of optimizing PSO-SVM-BP prediction model

预测模型计算过程的主要步骤如下。

1)原始数据的检验及预处理

受环境条件及不确定因素的影响，隧道变形监测数据一般具有非等距的特点，但预测模型要求数据为等时距，因此采用三次样条插值对原始非等距序列进行插值处理。同时，一般情况下，隧道监测数据都具有较大的随机性，规律性不强，某些节点具有一定的奇异性，需要对其进行一定的修正，使之成为规律性较强的序列，以利于后期预测，且修正方法为二次平滑法。

2)隧道变形的初步预测

采用支持向量机模型对隧道的变形进行初步预测，但支持向量机运算过程中的参数选择很大程度上依赖于使用者的经验，容易陷入局部最优解，因此采用粒子群算法对支持向量机进行全局优化，以增加预测过程的收敛速度和精度，实现对隧道变形的初步预测。

3)误差修正预测

由于任何模型均难以一次性拟合隧道的变形过程，为提高预测精度，或由于初步预测结果的精度不能满足期望要求时，可采用BP神经网络对其误差序列进行预测，达到误差修正的目的，并将预测结果与初步预测结果进行叠加，进而实现对隧道变形的综合预测。

1.2 基本原理

1)支持向量机

支持向量机(support vector regression，SVM)是基于统计理论提出的小样本学习方法，其主要思想是利用非线性映射将本空间问题映射到一个高维空间中，进而实现最优线性回归问题到凸规划问题的转变。同时，为降低运算过程中的维数灾难，支持向量机对核函数进行定义，即将高维空间的内积运算转变为原有空间的核函数运算。支持向量机能很好地解决高维数、非线性、小样本等问题，泛化能力较强，具有较强的适用性[10-12]。

若将n维空间的样本表示为{Xi,Yi}，且在超出误差ε下，采用线性函数(f(x)=ωx+b)对样本进行无误差拟合，并引入松弛变量ξi，ξi*(ξi≥0，ξi*≥0)，则可将回归求最小值问题转变为

(1)

(2)

式中：b为偏置量；ω为权重惯量；l为训练样本数；C为惩罚因子；ε为超出误差。

根据最优化原理，目标函数将凸二次规划问题转变为拉格朗日乘子αi*的对偶问题，且对偶问题的表达式为

(3)

(4)

进而，将函数f(x)表示如下：

(5)

式中：偏置量可以通过条件KTT求得，且αi-αi*≠0为对应xi的支持向量。

2)粒子群优化算法

粒子群优化算法(particle swarm optimization，PSO)是一种群体智能的随机优化算法，该算法是根据粒子在空间中的运动趋势进行调节，使其运动轨迹不断接近最优点。PSO算法在优化过程中的迭代公式为

vid(k)=ωivid(k-1)+c1rand1(pbesti-xid(k-1))+c2rand2(gbesti-xid(k-1)),

(6)

xid(k)=xid(k-1)-vid(k),i=1,2,…,n。

(7)

式中：m为粒子群规模；n为粒子维数；vid(k)为第k次迭代位移偏量；xid(k)为第k迭代步时的空间位置；c1，c2为搜索参数；rand1，rand2为介于0～1之间的随机数；ωi为惯性权重；pbesti为粒子的最优解；gbesti为第i步时种群的最优解。

同时，在粒子群算法的优化过程中，惯性权重对收敛速度及解的精确性具有较大影响，其值越大会导致收敛速度增加，但会牺牲解的精确性；其值越小可得到更优的解，但会降低收敛速度。因此，采用自适应调整惯性权重的粒子群算法对支持向量机进行优化。

3)BP神经网络

BP神经网络(backpropagation neural network)是一种多层前馈式的误差反传神经网络，一般为3层结构(见图2)，包含输入层、输出层及隐含层，其中隐含层具有单个或多个之分，各层含有若干相互独立的节点，层与层间的节点由相应的权值连接。BP神经网络的基本思想是利用正、反向传播，采用梯度下降法对连接权值进行修正，进而达到调整预测误差的目的，使其收敛值达到最小。同时，BP神经网络具有较强的信息处理功能，主要表现在并行处理能力强，容错性高，具有较好的组织、学习及适应能力，其优点是能很好地利用网络结构实现非线性映射，达到解决多维非线性问题的目的[13-15]。

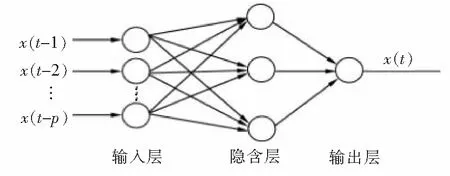
图2 BP神经网络结构图Fig.2 BP neural network structure

根据BP神经网络的基本原理，其训练步骤如下。

①对输入样本进行归一化处理，并对模型结构参数进行初始化，包括设定训练次数、隐含层节点数、初始权值阈值及学习精度等。

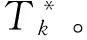
③利用梯度法对各层间的连接权值进行修正，并将输出值与期望值之间的误差表示为

(8)

模型的误差修正是对其连接权值进行调整，其权值修正函数为

ωij=ωij+Δωij=ωij+ηδqiγqi。

(9)

式中：η为学习因子；δqi为误差修正系数,q为第q个学习样本,i为隐含层或输出层节点。

④若训练误差达到期望的收敛误差，则停止训练；若训练误差未达到收敛误差，则进入误差反向传播阶段，即重复进入第③步，直到输出值与期望值之间的误差达到期望的收敛误差。

4)动态滚动预测

在隧道施工过程中，监测数据会随隧道施工的进行而不断增加或更新，且预测模型随预测周期的增加，其预测精度会有减弱的趋势，若将新监测的数据简单的加入到原始数据中，会使样本总量增加，增加训练量，减慢收敛速度。

因此，采用实时跟踪法，将新增加的数据替换等量的旧数据，并保持样本总量的不变，且对预测过程中的参数进行适应性调整，进而得到新的变形预测值，达到动态预测的目的。具体操作过程如下：

①若原始变形序列总共具有n个监测数据，即{1,2，…，p，…，n}，但随着监测过程的持续，新监测得到p个数据。

②为保证预测样本总数的不变，将新增的p个序列替换原序列的前p个序列，即将新序列表示为{p+1，…，n，n+1，…，n+p}，进而对新序列进行预测分析，以达到实时跟踪预测。

2 实例分析

2.1 工程概况

为验证预测模型的有效性，采用文献[7]中的实例进行检验。大相岭隧道隧址区的断层较为发育，使得隧址区岩体的节理发育，加之开挖过程造成应力释放，促使围岩出现松弛，导致围岩的大变形。该隧道右线YK62+900—YK63+100区间发育有3条较大的断层破碎带，围岩以Ⅳ级的凝灰岩及岩碎屑为主，地下水丰富，且在施工过程中，出现了涌水现象，导致围岩及支护结构出现较大变形，对现场施工安全造成了一定的影响。为实时掌握该区域隧道的变形特征，在该破碎区布置了若干监测断面，选择其中ZK63+010和ZK63+070断面的监测数据作为预测模型的验证数据，变形值详见表1。两断面共监测了22个周期，每个监测周期的时间为1 d，其中ZK63+010断面的累计变形量为20.1 mm，ZK63+070断面的累计变形量为21 mm。

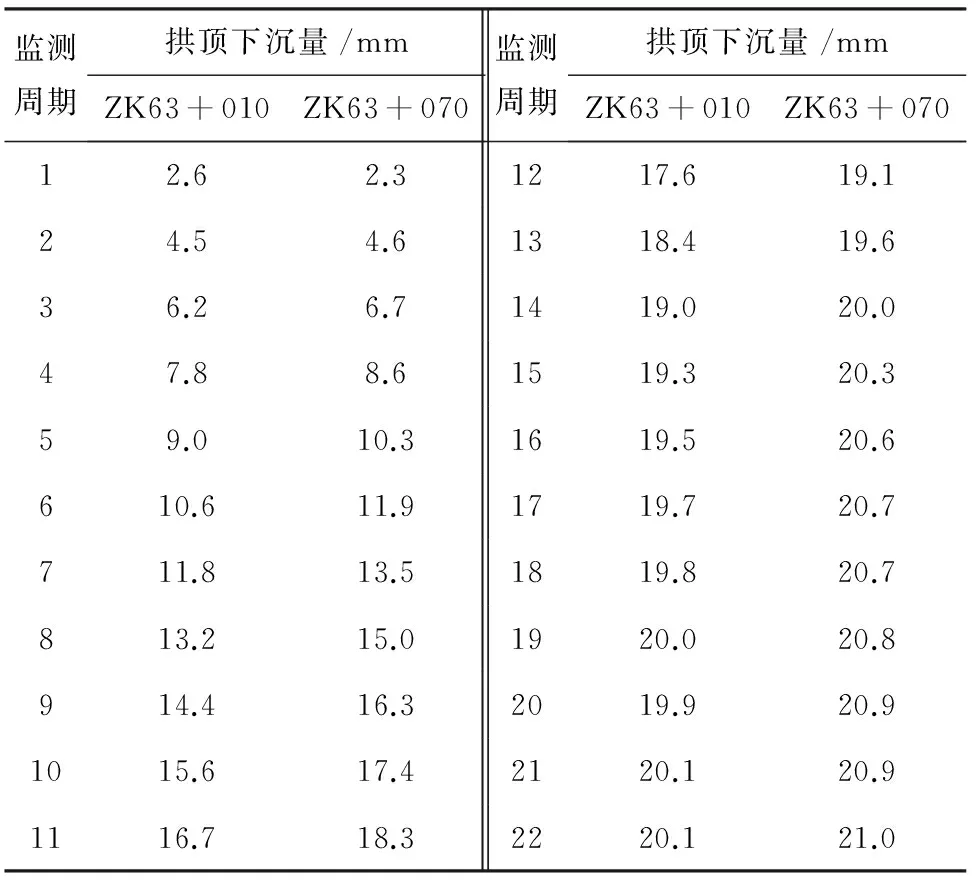
表1 隧道变形监测数据

为进一步分析隧道的变形特征，对两断面的变形速率作图，见图3。根据隧道变形的速率图，得出两断面的变形速率均具有持续减小的特征，但ZK63+010断面的变形速率波动性相对更强，主要是在第5—10监测周期之间的波动较明显，而ZK63+070断面的变形速率曲线相对较平缓，波动性较弱。

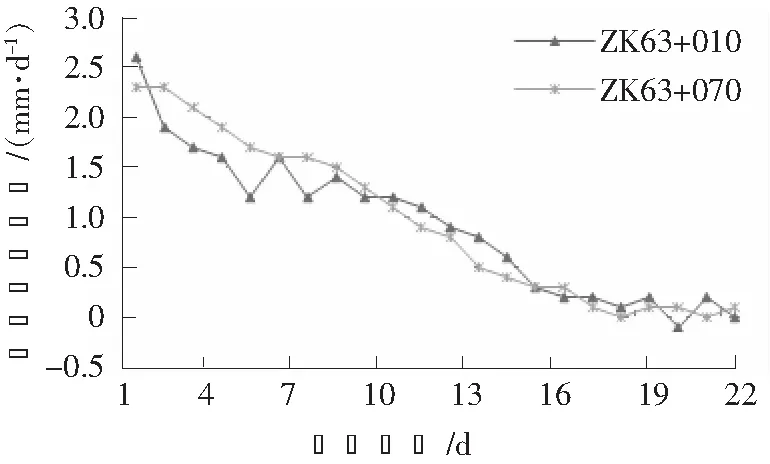
图3 隧道变形速率曲线图Fig.3 Deformation rate curve of the tunnel

同时，再进一步对变形速率的特征参数进行统计，详见表2。对比ZK63+010和ZK63+070断面的特征参数，得出前者比后者的最大变形速率要大，这与前者变形速率的波动性关系较大。

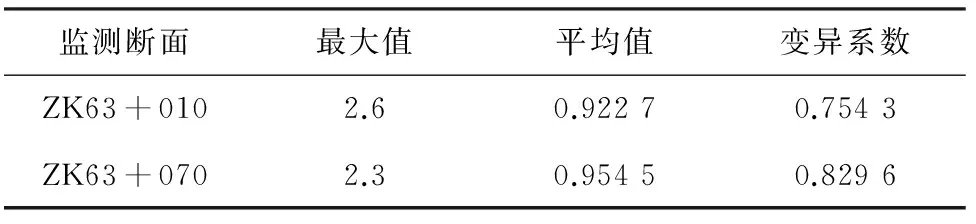
表2 变形速率的特征参数

同时，ZK63+010断面的平均变形速率相对更小，但ZK63+070的变异系数更大，说明后者的离散程度相对更高。同时，为充分达到研究预测模型有效性的目的，将ZK63+010断面的监测数据作为初步分析数据，而将ZK63+070断面的监测数据作为验证分析数据。

2.2 隧道变形位移预测

由前文对隧道变形特性的分析，得出实例数据均为等距序列，且稳定性较好，因此不用对其进行插值或平滑处理。根据PSO-SVM-BP预测模型的基本原理编制MATLAB程序，并根据相关文献的研究成果及使用经验设定相关参数[3-6]，如将粒子群优化支持向量机的学习因子(c1，c2)设定为2，惯性权重区间为0.4～0.9，最大迭代数为1 500，维数设定为10等；而BP神经网络的最小训练速率设定为0.9，动态参数为0.7，迭代次数为1 000，训练函数为train函数等。再将样本分为训练样本和验证样本，其中第1—16个周期的监测数据为训练样本，剩余样本为验证样本。经过预测，得到隧道变形初步预测的结果如表3所示。

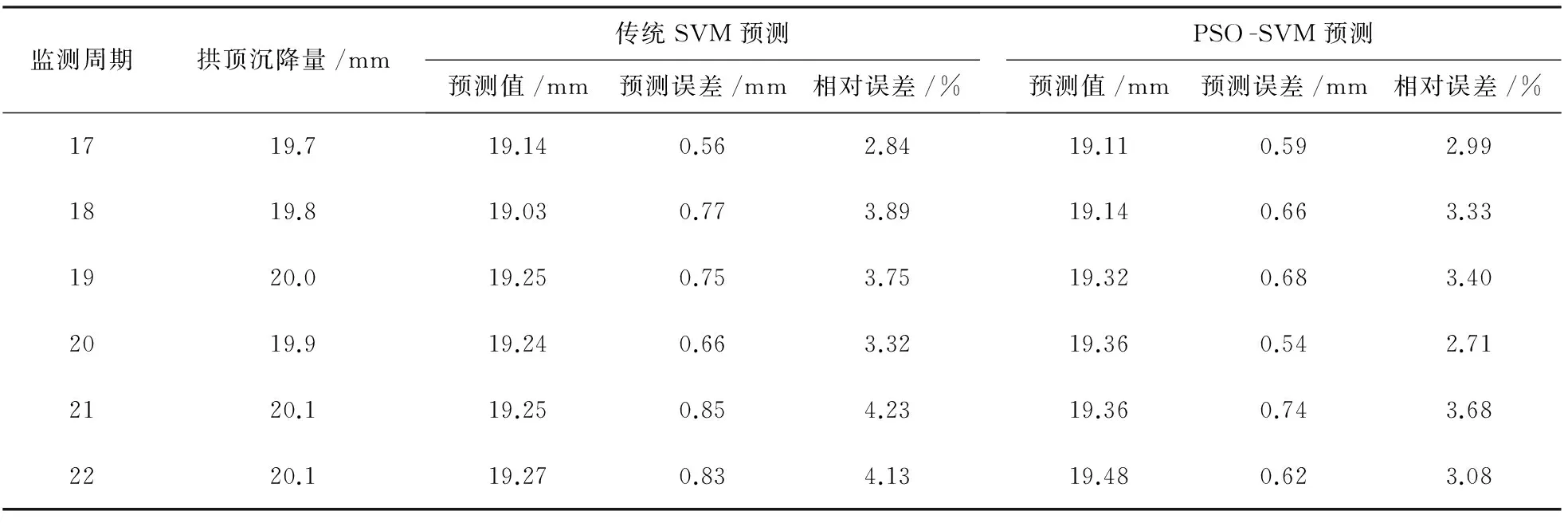
表3 初步预测值与实测值比较

对比两预测模型在不同节点的预测结果，均以PSO-SVM模型的预测相对误差更小，预测结果更优。其中，两者的最大相对误差分别为4.23%和3.68%，平均相对误差分别为3.69%和3.20%，显然，PSO-SVM模型较传统的SVM模型具有更高的预测精度。同时，两预测模型的最大相对误差均出现在第21个预测周期，且后两周期相对前几个周期的预测误差更大，这说明随预测时步的增加会降低预测精度。另外，总体评价初步预测结果发现，各节点的相对误差均小于5%，说明预测精度相对较高，预测模型参数设置较为合适。为进一步提高预测精度，结合预测思路，再利用BP神经网络对误差序列进行修正预测。

在BP神经网络的误差修正预测过程中，隐含层节点对预测精度及收敛速率具有较大影响，因此采用试算法确定最优隐含层节点数，且节点数区间设定为7～14，试算结果如表4所示。

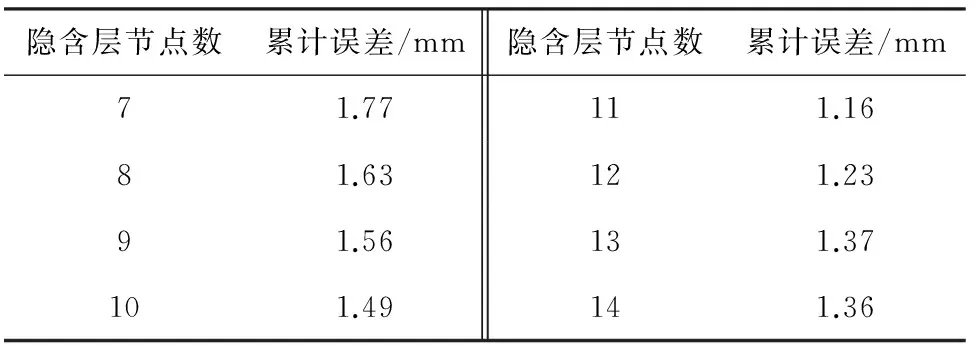
表4 隐含层节点试算结果

根据试算结果，随隐含层节点的增加，累计误差表现为先减小再增大的趋势。其中，节点数为7时的累计误差最大，为1.77 mm；节点数为11时的累计误差最小，为1.16 mm。因此将BP神经网络的隐含层节点数设置为11。同时，节点数为11～14时的累计误差均不同程度的小于节点数7～10时的累计误差，说明节点数越大，会牺牲一定的收敛速度，但预测精度相对更优。

当隐含层节点数为11时，BP神经网络的修正预测结果如表5所示。由表5可知，各预测节点的残差值均较大，修正预测的预测精度不及初步预测的预测精度，这与误差序列含有较大的随机性和不确定性有关，其中最大残差值为0.25 mm，最小残差值为0.16 mm，两者相差不大。

表5 BP神经网络的修正预测结果

综合前文预测，得到隧道ZK63+010断面的变形预测结果如表6所示。预测模型在ZK63+010断面17—22周期预测的最大及最小相对误差分别为1.26%和0.80%，平均相对误差为0.97%，预测精度较高，说明预测模型是成功的。

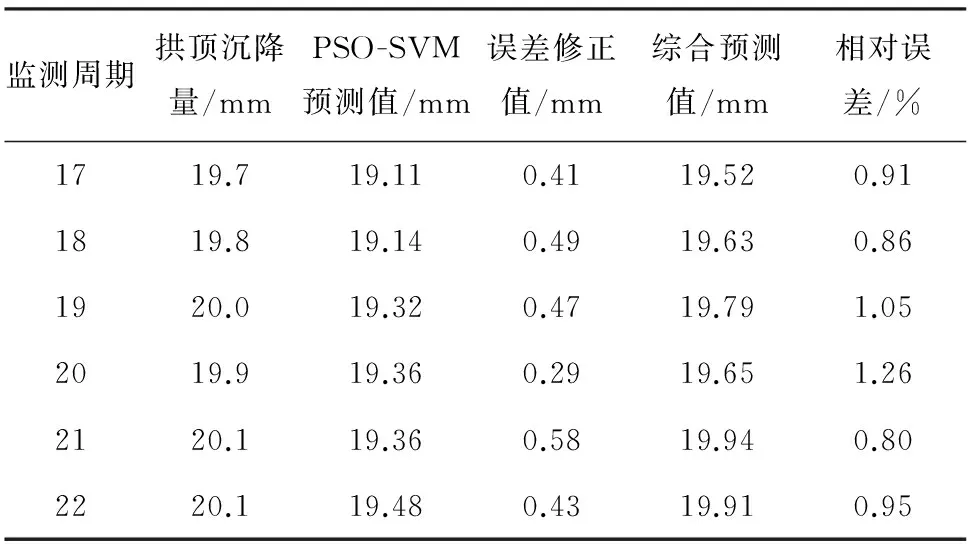
表6 ZK63+010断面变形预测结果

2.3 预测模型的有效性检验

由于预测模型所需的信息是相对的，且隧址区的地质条件较复杂，变形破坏方式具有多样性，为验证预测模型的有效性和适用性，再对ZK63+070断面的变形进行预测，预测结果如表7所示。由表7可知ZK63+070断面的最大及最小相对误差分别为1.2%和0.62%，平均相对误差为0.94%，要略优于ZK63+010断面的预测结果，这与ZK63+070断面的变形特征更加稳定有关。通过对该断面的变形预测，证明预测模型的预测精度较高，适用性较强。

为进一步分析两断面在不同预测阶段的差异，再进一步对两断面在不同预测阶段的残差进行统计，对比分析两者的预测特征，结果如图4、图5所示。在初步预测阶段，两断面的残差值多在0.5～0.7 mm之间，ZK63+010断面的残差值均大于ZK63+070断面的残差值，这与前者的变形速率波动较大有关，其波动又受施工的影响，进而也说明预测模型一定程度上也受施工扰动的影响。在修正预测阶段，两断面在各节点的预测残差波动性较大，得出该预测过程受初步预测阶段误差序列随机性的影响较大，说明监测过程中的不确定因素也对预测模型具有一定的影响。

表7 ZK63+070断面变形预测结果

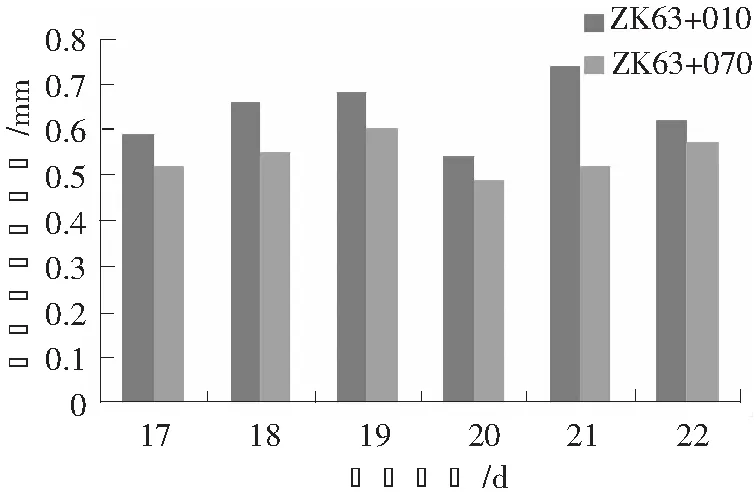
图4 初步预测阶段残差值对比Fig.4 Comparison of residual values in preliminary prediction

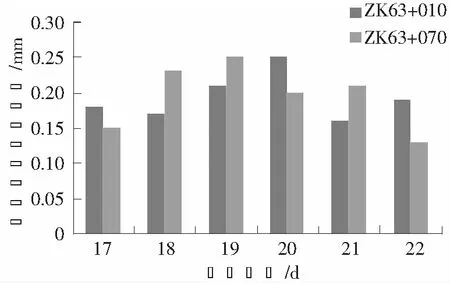
图5 修正预测阶段残差值对比Fig.5 Comparison of residual values in modified prediction stage

另外，再进一步将预测结果与文献[7]进行对比分析，结果如表8所示。由表8可知，对比对应断面在不同节点处的相对误差，得出本文预测模型的预测精度更高。同时，ZK63+010和ZK63+070断面预测过程中的相对误差的平均值分别为0.97%和0.94%，方差值分别为0.027 0和0.050 3；而在文献[7]中相对误差的平均值分别为1.02%和4.22%，方差值分别为1.286 2和1.058 0。综合对比，预测结果较文献[7]具有更高的预测精度，且预测结果具有更好的稳定性。

表8 不同预测模型的对比分析

3 结 论

1)粒子群优化支持向量机-BP神经网络模型考虑了隧道变形数据中的随机性和不确定性，并能根据监测数据的不断更新，实现滚动预测，客观地反映出隧道的变形发展趋势，对及时优化和调整现场施工、保证隧道的稳定具有重要的参考价值。

2)预测模型在初步预测阶段的预测相对误差均小于5%，通过BP神经网络的误差修正，使得预测精度进一步提高，最终预测结果与实测值较为接近，预测精度较高，稳定性较好。

3)通过对比不同断面及相关文献的预测结果可知，预测模型具有更好的稳定性，适用性较强，且很大程度上提高了预测精度，验证了预测思路的有效性。

4)预测模型具有理论清晰、结构简单、预测精度高等优点，对隧道变形预测具有很好的适用性，也可应用到岩土工程的其他领域。但其预测结果受监测数据中不确定误差因素的影响较大，对现场监测数据的真实性要求较高，值得深入研究。

5)本文仅验证了PSO-SVM-BP预测模型在正常变形条件下的预测效果，其在大变形、突水、岩爆等特殊情况下的有效性仍有待进一步研究。

/References：

[1] 宁伟,周立,宁亚飞. 公路隧道监控围岩变形预测模型构建研究[J]. 测绘通报,2013(sup):103-107. NING Wei, ZHOU Li, NING Yafei. Study on construction of surrounding rock deformation prediction model for highway tunnel monitoring [J]. Bulletin of Surveying and Mapping, 2013(sup):103-107.

[2] 夏才初,那通兴,彭国才,等. 公路隧道施工变形监测精度要求探讨[J]. 隧道建设,2016,36(5):508-512. XIA Caichu, NA Tongxing, PENG Guocai, et al. Discussion on deformation monitoring accuracy of highway tunnel construction[J]. Tunnel Construction, 2016, 36(5): 508-512.

[3] 刘宇. 基于支持向量机的隧道变形预测模型研究[J]. 内蒙古科技大学学报,2015,34(4):370-373. LIU Yu. Research on tunnel displacement forecast model based on support vector machines [J]. Journal of Inner Mongolia University of Science and Technology, 2015, 34(4):370-373.

[4] 冯宝俊,刘敦文,褚夫蛟. 基于PSO-SVM模型的隧道水砂突涌量预测研究[J]. 中国安全生产科学技术,2014(7):123-129. FENG Baojun, LIU Dunwen, CHU Fujiao. Study on prediction of water and sand inrush quantity in tunnel based on PSO-SVM model [J]. Journal of Safety Science and Technology, 2014(7):123-129.

[5] 何延兵,刘辉. 红层蠕变特性及隧道围岩位移PSO-SVM预测研究[J]. 公路工程,2016,41(2):75-79. HE Yanbing, LIU Hui. Creep characteristics of red layer and tunnel surrounding rock displacement prediction based on PSO-SVM [J]. Highway Engineering, 2016, 41(2):75-79.

[6] 范思遐,周奇才,熊肖磊,等. 基于粒子群与支持向量机的隧道变形预测模型[J]. 计算机工程与应用,2014,50(5):6-10. FAN Sixia, ZHOU Qicai, XIONG Xiaolei, et al. Tunnel deformation prediction model based on support vector machine with particle swarm optimization algorithm [J]. Computer Engineering and Applications, 2014, 50(5):6-10.

[7] 张志强,李化云,阚呈,等. 大相岭隧道断层破碎带围岩变形的GA-BP神经网络预测技术[J]. 现代隧道技术,2014(2):83-89. ZHANG Zhiqiang, LI Huayun, KAN Cheng,et al. Prediction of surrounding rock deformation of the Daxiangling tunnel in fault zones using the GA-BP nerve network technique [J]. Modern Tunnel Technology, 2014(2):83-89.

[8] 龙浩,高睿,孔德新,等. 基于BP神经网络-马尔科夫链模型的隧道围岩位移预测[J]. 长江科学院院报,2013,30(3):40-43. LONG Hao, GAO Rui,SUN Dexin, et al. Forecast of tunnel’s surrounding rock displacement by BP neural network and Markov chain [J].Journal of Yangtze River Scientific Research Institute, 2013, 30(3):40-43.

[9] 张正虎,袁孟科,邓建辉,等. 基于改进灰色-时序分析时变模型的边坡位移预测[J]. 岩石力学与工程学报,2014,33(sup2):3791-3797. ZHANG Zhenghu, YUAN Mengke, DENG Jianhui, et al. Displacement prediction of slope based on improved grey-time series time-varying model [J].Chinese Journal of rock mechanics and engineering, 2014, 33(sup2): 3791-3797.

[10]李方伟,罗嘉,朱江,等. 一种基于混合核函数PSO-SVM的网络安全态势预测方法[J]. 微电子学与计算机,2015,32(12):110-115. LI Fangwei, LUO Jia, ZHU Jiang, et al. A method of network security situation prediction based on hybrid kernels PSO-SVR [J]. Microellectronics & Computer, 2015, 32(12):110-115.

[11]周奇才,范思遐,赵炯,等. 基于改进的支持向量机隧道变形预测模型[J]. 铁道工程学报,2015(3):67-72. ZHOU Qicai，FAN Sixia, ZHAO Jiong, et al. Tunnel deformation prediction based on modified support vector machine [J]. Journal of Railway Engineering Society, 2015(3): 67-72.

[12]李晓龙,魏丹,王复明. 基于线性规划支持向量机的隧道围岩变形预测[J]. 中外公路,2009,29(4):157-162. LI Xiaolong, WEI Dan, WANG Fuming. Deformation prediction of tunnel surrounding rock based on linear programming support vector machine [J]. Journal of China & Foreign Highway, 2009,29 (4): 157-162.

[13]王树栋,刘开云. 长大隧道软弱围岩施工大变形智能预测方法[J]. 中国铁道科学,2008,29(2):82-87. WANG Shudong, LIU Kaiyun. Intelligence method for large deformation prediction of weak surrounding rock construction in long and large tunnel [J]. China Railway Science, 2008, 29(2): 82-87.

[14]胡斌,冉秀峰,祝凯,等. 基于BP人工神经网络的隧道围岩力学参数反分析[J]. 铁道建筑,2016(7):70-73. HU Bin, RAN Xiufeng, ZHU Kai, et al. Inverse analysis of tunnel surrounding rock mechanical parameters based on BP(back propagation) artificial neural network [J]. Railway Engineering, 2016(7): 70-73.

[15]杨友元. 高速铁路隧道施工中监控量测探析[J]. 河北工业科技,2009,26(4):273-276. YANG Youyuan. Study on monitoring of high-speed railway tunnel construction [J]. Hebei Journal of Industrial Science and Technology, 2009, 26(4): 273-276.

Application of support vector machine model in fracture zone surrounding rock deformation prediction

REN Qingguo, MIAO Landi

(Shaanxi Railway Institute， Weinan, Shaanxi 714000， China)

The prediction of surrounding rock deformation is an important basis for the safety evaluation of the tunnel and the construction of the later stage. In order to improve the precision of the deformation prediction, by combining with the engineering practice, the idea of PSO-SVM-BP prediction model is put forward. First of all, the deformation data are pre processed by three spline interpolation and smoothing method for two times, laying the foundation for the late deformation prediction; secondly, to optimize the parameters of support vector machine based on particle swarm algorithm, then PSO-SVM model is established, and the surrounding rock deformation is predicted preliminarily; at last, a BP neural network for error correction is used to achieve comprehensive forecasting purposes, and engineering examples are used for the test to verify the effectiveness of the prediction model. The results show that the relative error of preliminarily prediction results is all less than 5%, and the prediction accuracy after error correction increases to 0.97%, showing higher prediction accuracy, which proves the validity of the forecast model. The prediction model is feasible, and can provide a reference for similar research.

tunnel engineering; particle swarm algorithm; support vector machine; BP neural network; dynamic prediction

1008-1534(2017)03-0194-08

2017-03-03;

2017-03-14；责任编辑：冯 民

任庆国(1980—)，男，山东曹县人，讲师，硕士，主要从事桥梁施工技术与控制方面的研究。

E-mail:17969095@qq.com

U452.1+2

A

10.7535/hbgykj.2017yx03008

任庆国，苗兰弟.支持向量机模型在断层破碎带围岩变形预测中的应用[J].河北工业科技,2017,34(3):194-201. REN Qingguo, MIAO Landi.Application of support vector machine model in fracture zone surrounding rock deformation prediction[J].Hebei Journal of Industrial Science and Technology,2017,34(3):194-201.