基于倾角影响线的简支梁桥损伤识别
2017-06-15张延庆吴贵飞邓洪亮
张延庆,吴贵飞,邓洪亮
(北京工业大学建筑工程学院,北京 100124)
基于倾角影响线的简支梁桥损伤识别
张延庆,吴贵飞,邓洪亮
(北京工业大学建筑工程学院,北京 100124)
为了推广影响线理论在结构损伤识别方面的应用,提出了一种基于简支梁桥损伤前后倾角影响线差值及差值曲率的损伤识别方法。对简支梁桥倾角影响线的概念进行定义,推导了简支梁桥损伤前后的倾角影响线公式,并对损伤识别指标进行公式推导,从理论上证明了将其用于损伤识别的可能性。为验证本文建立损伤识别指标的正确性,建立简支梁桥结构有限元模型进行分析。结果表明:简支梁桥损伤前后的倾角影响线差值在损伤区域出现峰值;简支梁桥损伤前后的倾角影响线差值曲率在无损伤区域均为0,在损伤区域均不为0。分析得出结论如下:简支梁桥损伤前后的倾角影响线差值用于判别损伤位置准确度较高;利用简支梁桥损伤前后的倾角影响线差值曲率不仅对单处损伤和多处损伤均具有良好的识别效果,而且可以实现对简支梁桥损伤程度的识别。
桥涵工程;简支梁桥;倾角影响线;损伤识别;差值;曲率
梁桥结构在其使用过程中,由于受到各种因素的影响,结构损伤逐渐积累。如何对梁桥结构出现的损伤进行识别并加以控制,一直是人们研究的重要课题[1-3]。现行的损伤识别检测方法主要有基于挠度的损伤识别、基于模态的结构损伤识别[4-5]以及基于人工智能的损伤识别方法[6-8]等。随着影响线理论[9]的不断发展,利用位移影响线的差值及曲率对简支梁桥进行损伤识别检测[10-14],具有操作简单、经济适用的特点。随着倾角仪的不断发展[15],倾角的测量精度不断提高[16],利用结构倾角位移实测值对桥梁进行损伤识别检测成为可能。
本文提出倾角影响线的概念,推导了简支梁桥结构损伤前后的倾角影响线公式,在此基础上提出基于倾角影响线差值的损伤识别指标,并通过数值模拟结合有限元方法建立简支梁桥结构模型,进行结构的损伤识别分析,验证所建立的损伤识别指标的有效性。
1 简支梁倾角影响线
单位集中荷载沿结构移动时某一指定量值变化规律的图形称为该量值的影响线。在梁上确立某观测点,当集中荷载在梁桥上移动时,测量该观测点的倾角变化值,其倾角的变化规律称为该梁的倾角影响线。
图1所示为无损伤时的简支梁结构模型,跨长为l,假定截面尺寸及材质相同,弯曲刚度取EI。

图1 简支梁倾角影响线Fig.1 Angular influence line of simply-supported beam
设立倾角观测点S,观测点与支座A的距离为s,将车辆在简支梁桥上的移动简化为集中荷载FP,荷载距支座A的距离为x。根据能量原理中的单位荷载法,利用式(1)可求得观测点S的倾角影响线θS(x)公式,该公式与荷载的移动位置x有关。为了区分与移动荷载的位置关系,代入过渡坐标系x′。
(1)

(2)
(3)
将式(2)、式(3)代入式(1),得到简支梁在观测点S处的倾角影响线公式:
(4)
由式(4)可知,简支梁的倾角影响线是以观测点S为界的分段连续函数,而且倾角影响线不仅与荷载移动位置有关,而且与观测点的选取有关,说明选取合适的测点位置能够提高测量结果的准确性。
2 存在局部损伤时简支梁桥的倾角影响线
2.1 存在局部损伤时简支梁桥的倾角影响线理论公式
桥梁若发生损伤,必然会引起结构截面特性的变化,因此,在进行存在局部损伤的简支梁桥倾角影响线求解时,用损伤区段截面刚度的降低来模拟桥梁出现损伤,刚度折减系数取k。图2所示为存在局部损伤时的简支梁桥结构模型,损伤区间为(a,b),损伤区段的截面刚度为kEI,其中:k∈{0,1},当k=0时表示该区段完全损坏,当k=1时表示结构完好无损伤。简支梁桥的其他参数均与图1相同。
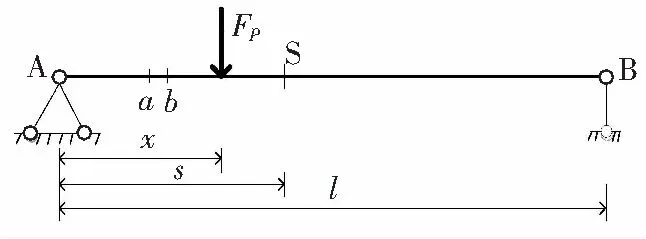
图2 存在局部损伤的简支梁桥结构模型Fig.2 Simple supported beam structure model with local damage

如图2所示,选取的倾角观测点S位于损伤位置右侧,即s>b,此时存在局部损伤时的简支梁桥结构的倾角影响线公式为
θS(x)=θSs(x)+Δθab(x)。
(5)
式中:θSs(x)表示简支梁无损伤时移动荷载下的倾角影响线公式,见式(4);Δθab(x)表示与局部损伤相关数值的公式,表达式如下:
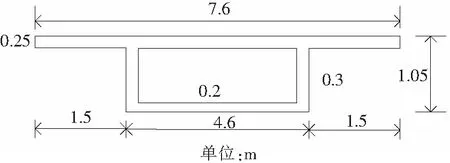
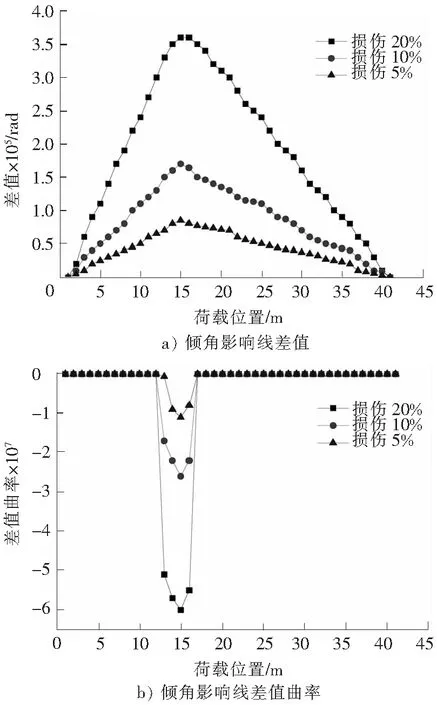
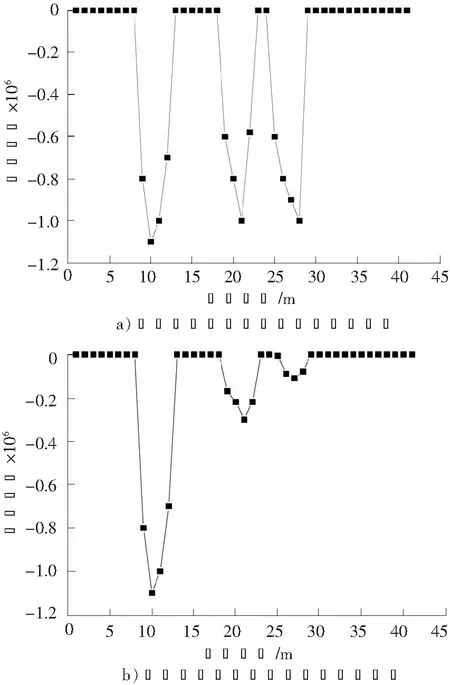
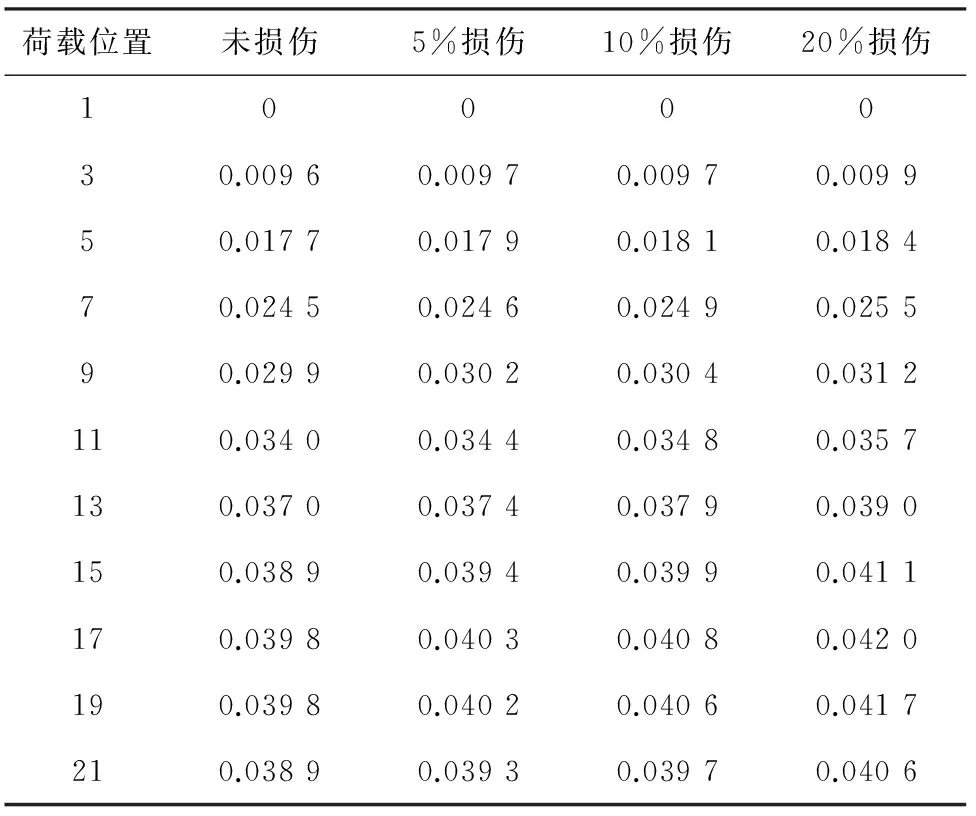
当0≤x (6) 当a≤x≤b时, (7) 当b (8) 需要说明的是,上述公式为观测点S位于损伤右侧(图2)的情况,当观测点位于损伤区域及损伤左侧时,简支梁桥结构的倾角影响线公式与上述求解过程相同,不再赘述。 2.2 基于倾角影响线差值的损伤识别指标 从式(5)可以看出,损伤后的倾角影响线公式由两部分组成,θSs(x)为简支梁桥未损伤时的倾角影响线公式,则Δθab(x)可以看作是损伤前后观测点S的倾角影响线差值公式。从Δθab(x)的表达式可以看出,简支梁桥在未损伤区域的倾角影响线差值为荷载移动位置的线性函数(式(6)、式(8)),而在损伤区段为变量的三次函数(式(7)),且该曲线的峰值出现在损伤区段,因此可以用来进行识别损伤。 根据上述分析,直接对损伤前后倾角影响线的差值进行研究。根据倾角影响线差值公式Δθab(x),当0≤x 2.3 基于倾角影响线差值曲率的损伤识别指标 根据曲率公式(9),对于实际梁桥结构,其变形非常微小,观测点的倾角影响线差值的一阶导数的平方几乎接近于0,可以忽略不计,因此倾角影响线差值的曲率可以用差值公式的二阶导数Δθ″ab(x)表示。 (9) 根据式(6)—式(8),当倾角观测点S位于损伤区域右侧时,其差值曲率如下: 当移动荷载位于简支梁桥结构无损伤区域时: Δθ″ab(x)=0。 (10) 当移动荷载位于简支梁桥结构损伤区域时: (11) 可以看出,倾角影响线差值曲率公式与损伤位置和损伤程度有关,而与观测点的选取无关,说明可以利用该指标对简支梁桥结构进行损伤位置识别分析。同时,利用倾角影响线差值曲率识别出损伤位置后,根据公式可以推算出刚度折减系数的数值,因此可以识别出损伤程度。 为了验证利用倾角影响线建立的损伤识别指标的正确性,建立40 m跨混凝土结构简支梁模型,节点间距为1 m,共41个节点,40个单元。桥梁采用C40混凝土,弹性模量E=3.25×107kN/m2,截面如图3所示,惯性矩I=0.453 4 m4,影响线加载采用荷载FP=1×105N。 图3 横截面示意图 Fig.3 Cross section 3.1 简支梁桥出现单处损伤的识别 为观察简支梁桥结构未损伤时的实测倾角影响线,分别建立梁端支座(测点1)、简支梁1/4跨(测点2)及跨中位置(测点3)3个观测点测量无损伤简支梁在移动荷载下的实测倾角影响线,如图4所示。可以看出,测点选择越靠近简支梁支座处,倾角影响线的数值越大,识别度也越高,说明测点越靠近支座位置,利用倾角传感器进行倾角测量所得的测量结果准确性越高。结合现有倾角传感器的测量精度,进行实测时应该尽量选择靠近支座位置安放倾角传感器。同时从图4还发现,当测点选取靠近跨中位置时,简支梁倾角影响线的数值出现变号的情况。 图4 简支梁无损伤时的倾角影响线Fig.4 Angular influence line of simple-supported beam without damage 根据上述分析,在简支梁桥支座处放置倾角传感器,测量简支梁出现局部损伤时梁端的倾角影响线。利用倾角影响线差值及差值曲率进行损伤识别分析。简支梁桥损伤模拟采用区段刚度降低的方法,设定损伤区域(0.3~0.4)l,在损伤区域分别设定20%,10%,5%等3种损伤程度。利用倾角影响线进行损伤识别的结果如图5所示。 图5 简支梁桥的损伤识别曲线Fig.5 Damage identification curve of simple-supported beam 图5 a)表示利用倾角影响线差值进行损伤识别。可以看出,倾角影响线差值在损伤区段出现峰值,且峰值大小与损伤程度有很大关系,损伤程度越大,识别敏感性越高,说明利用该指标可以对简支梁桥进行损伤位置的识别。 图5 b)表示简支梁桥出现局部损伤时的倾角影响线差值曲率,利用式(12)求得。可以看出,在无损伤区域,简支梁桥结构的倾角影响线差值曲率均为0,而在损伤区域差值曲率值均不为0,因此可以利用倾角影响线差值曲率对简支梁桥进行损伤定位。随着损伤程度的降低,倾角影响线差值曲率值逐渐变小,根据损伤区域倾角影响线差值曲率曲线的峰值,利用式(11)可以反推出刚度折减系数k的大小,据此可以判断出损伤程度的大小。 (12) 3.2 简支梁桥多处位置损伤时的识别 通过上述分析,利用倾角影响线建立的损伤识别指标对单个位置损伤的识别效果较好,可以明显地判断出损伤位置。现研究简支梁桥出现多处损伤的情况。简支梁桥分析模型仍采用上述结构分析模型,分别在简支梁桥(0.2~0.3)l,(0.45~0.55)l,(0.6~0.7)l处设定损伤位置,损伤程度均为20%,倾角观测点仍选择简支梁桥支座处。分析结果如图6 a)所示。可以看出,在无损伤区域,简支梁桥结构的倾角影响线差值曲率均为0,而在损伤区域差值曲率值均不为0,说明利用倾角影响线差值曲率损伤识别指标可以对多处损伤程度相同的情况进行损伤位置判定。由于3处损伤的损伤程度均为20%,所以理论上3处的影响线差值曲率应该近似相等,但是从图6 a)可以看出,其倾角位移影响线差值曲率数值并不相等,说明损伤之间是有影响的,所以对于多损伤的情况,倾角影响线差值曲率损伤识别指标可以进行损伤定位,对于损伤程度的判定会有一定误差。 图6 简支梁桥多处损伤时倾角影响线差值曲率Fig.6 Difference curvature of angular influence line of simply supported beam with multiple damage 图6 b)表示3处损伤程度不相同时的倾角影响线差值曲率。损伤位置仍在简支梁桥(0.2~0.3)l,(0.45~0.55)l,(0.6~0.7)l等3处,其损伤程度分别设定为20%,10%,5%。由图可知,在损伤区域的倾角影响线差值曲率均不为0,说明利用倾角影响线差值曲率损伤识别指标可以对简支梁桥多处出现不同程度的损伤情况进行损伤定位,能够明显地判断出损伤区域,损伤识别效果较好。 3.3 灵敏度分析 上述分析所得数据是在理想情况下通过数值分析得到的,倾角取值为小数点后6位。现有高精度倾角传感器的精度一般为0.001°,分辨率为0.000 5,探究将倾角数值取小数点后4位有效数字时对损伤识别的影响。以支座处的倾角影响线为例,损伤位置(0.3~0.4)l,提取损伤程度分别为未损伤、5%损伤、10%损伤、20%损伤时部分荷载移动时的支座倾角影响线数值,结果如表1所示。 表1 不同荷载位置支座倾角影响线数值 可以看出,当倾角取小数点后4位有效数字时,不同的损伤情况测出的数值有明显变化,并且同一损伤状况下不同荷载位置的倾角影响线数值也有明显的变化规律,说明在此精度下可以利用倾角影响线进行损伤识别检测。相比常规倾角传感器,其具有更高的灵敏度,测试结果更加精确。 1)利用损伤前后的倾角影响线差值可以实现对简支梁桥的损伤识别,差值曲线在损伤区域出现峰值,具有良好的损伤识别效果。 2)简支梁桥损伤前后的倾角影响线差值曲率在无损伤区域均为0,在损伤区域均不为0,据此进行简支梁桥结构的损伤识别,准确度高,且对单处损伤和多处损伤均可进行损伤识别。不仅可以识别损伤位置,同时利用倾角影响线差值曲率公式可以实现对损伤程度的判定。 3)根据简支梁桥的结构特点及现有高精度倾角传感器的精度要求,进行倾角实测时的测点选择应尽量靠近支座附近,可以增加准确度。 4)用倾角影响线方法对简支梁桥结构进行损伤识别仅需要一个倾角传感器即可完成操作,方法简便,经济实用,便于工程推广。 /References: [1] 刘效尧,徐岳.桥梁[M]. 2版.北京:人民交通出版社,2011. [2] 向天宇,赵人达,刘海波. 基于静力测试数据的预应力混凝土连续梁结构损伤识别[J]. 土木工程学报,2003,36(11):79-82. XIANG Tianyu,ZHAO Renda,LIU Haibo. Identification methods for different structural damage based onfrequency response [J].China Civil Engineering Journal, 2003, 36(11):79-82. [3] ZHANG Z, AKTANA E. Different levels of modeling for the purpose of bridge evaluation [J]. Applied Acoustics, 1997, 50(3): 189-204. [4] OVANESOVAA V, SUAREZL E. Applications of wavelet transform: Applications to damage detection in framestructures[J]. Engineering Structures, 2004, 26(1): 39-49. [5] 荆龙江,项贻强.基于柔度矩阵法的大跨斜拉桥主梁的损伤识别[J].浙江大学学报:工学版,2008,42(1):164-169. JING Longjiang, XIANG Yiqiang.Damage identification of main girders for long span cable-stayed bridge based on flexibility matrix[J]. Journal of Zhejiang University: Engineering Science, 2008, 42(1):164-169. [6] CHOI M Y, KWON I B. Damage detection system of a real steeltruss bridge by neural networks[J]. Earthquake Engineering,2000, 3988:295-306. [7] BARTHORPE R J, WORDEN K. Classification of multisite damage using support vector machines[J].Journal of Physics:Conference Series 305, 2011: 012059. [8] 刘洪公,王学军,李冰莹,等.基于卷积神经网络的桥梁裂缝检测与识别[J].河北科技大学学报,2016,37(5):485-490. LIU Honggong,WANG Xuejun,LI Bingying,et al. Detection and recognition of bridge crack based on convolutional neural network[J].Journal of Hebei University of Science and Technology,2016,37(5):485-490. [9] 张延庆. 结构力学(上册)[M]. 北京:科学出版社,2011. [10]杜永峰,刘云帅,王晓琴. 基于挠度差值影响线曲率的简支梁桥损伤识别[J]. 桥梁建设,2009,38(4):80-83. DU Yongfeng, LIU Yunshuai, WANG Xiaoqin. Damage identification of simply-supported beam bridges based on influence line curvature of deflection differential values[J].Bridge Construction,2009,38(4):80-83. [11]李起航,张延庆,孙珂. 利用位移影响线对曲线桥进行损伤识别的影响因素研究[J]. 科学技术与工程,2015,15(8):115-120. LI Qihang, ZHANG Yanqing, SUN Ke. The analysis of influencing factors to the damage identification of curved bridge using the influence line of displacement[J]. Science Techno-logy and Engineering, 2015,15(8):115-120. [12]SUN Ke,ZHANG Yanqing. Analysis of displacement influence line characteristics of simply supported beam with local damage [C]//4th International Conference on Structures and Building Materials. Guangzhou:[s.n.], 2014:364-368. [13]孙珂,张延庆. 基于位移影响线曲率的小半径弯桥损伤识别[J]. 浙江大学学报:工学版,2016,50(4):727-734. SUN Ke,ZHANG Yanqing. Damage identification of small-radius curved bridge based on curvation of displacement influence line [J].Journal of Zhejiang University:Engineering Science,2016,50(4):727- 734. [14]HUANG J,SHENTON H W. Experimentally determined continuous displacement influence lines for bridges[C]// Structures Congress 2008: Crossing Borders. Vancouver:ASCE,2008:1-10. [15]侯兴民,杨学山,黄桥. 利用倾角仪测量桥梁的挠度[J].桥梁建设,2004(2):69-72. HOU Xingmin, YANG Xueshan, HUANG Qiao. Using inclinometers to measure bridge deflections[J].Bridge Construction,2004(2):69-72. [16]刘爱华,李邓化,董必政. 高精度双轴倾角检测装置的设计与实现[J].北京信息科技大学学报(自然科学版),2013,28(5):51-55. LIU Aihua, LI Denghua, DONG Bizheng. Design and implementation of high accuracy dual axis inclination detection device[J].Journal of Beijing Information Science and Technology University,2013,28(5):51-55. Damage identification of simply-supported beam bridges based on angular influence line ZHANG Yanqing, WU Guifei, DENG Hongliang (School of Architecture and Civil Engineering,Beijing University of Technology,Beijing 100124,China) In order to promote the application of the influence line theory in structural damage identification, the damage identification indexes based on difference and difference curvature of angular influence line before and after the damage of the simply-supported beam bridges are proposed. The concept of angular influence line of simply-supported beam bridges is defined, the formula of angular influence line before and after the damage of the simply-supported beam bridges is derived, the formula of new damage identification indexes is deduced, and the feasibility of using the new damage identification indexes for damage identification is theoretically proved. To verify the correctness of the new damage identification indexes, the finite element model of simply-supported beam bridge is established. The result shows that the difference of angular influence line before and after the damage of the simply-supported beam bridges has a peak value in damage area; the difference curvature of angular influence line before and after the damage of the simply-supported beam bridges is 0 in the non-damage area, and not 0 in the damage area. The conclusion is that the difference of angular influence line before and after the damage of the simply-supported beam bridges can be used to determine the location of damage with high accuracy. By using the difference curvature of angular influence line, it not only has the good recognition effect to the single damage and multiple damage, but also can realize the recognition of the damage degree of the simply-supported beam bridges. bridge engineering; simply-supported beam bridges; angular influence line; damage identification; difference; curvature 1008-1534(2017)03-0177-06 2017-02-25; 2017-04-28;责任编辑:冯 民 张延庆(1958-),男,山东茌平人,教授,博士,博导,主要从事工程结构数值分析、结构优化、位移影响线等方面的研究。 E-mail:zhyq@bjut.edu.cn U441 A 10.7535/hbgykj.2017yx03005 张延庆,吴贵飞,邓洪亮.基于倾角影响线的简支梁桥损伤识别[J].河北工业科技,2017,34(3):177-182. ZHANG Yanqing,WU Guifei,DENG Hongliang.Damage identification of simply-supported beam bridges based on angular influence line[J].Hebei Journal of Industrial Science and Technology,2017,34(3):177-182.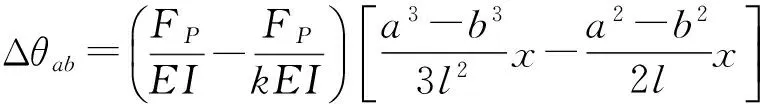

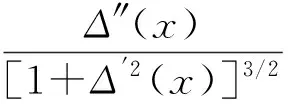
3 存在局部损伤的简支梁桥结构损伤识别分析

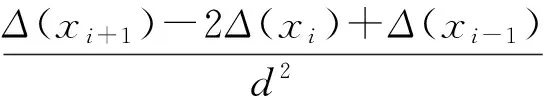
4 结 论
