具有自扩散的两种群互惠模型解整体存在及稳定性

江祥花,成晓燕,肖文斌

(1. 镇江高等专科学校 丹阳师范学院,江苏 丹阳 212300; 2. 扬州大学 数学科学院,江苏 扬州 225002)

具有自扩散的两种群互惠模型解整体存在及稳定性

江祥花1,成晓燕2,肖文斌2

(1. 镇江高等专科学校 丹阳师范学院,江苏 丹阳 212300; 2. 扬州大学 数学科学院,江苏 扬州 225002)

考虑生物数学中具有自扩散的两种群互惠模型,利用能量估计方法给出两种群互惠模型整体解的存在唯一性,并通过构造Lyapunov函数讨论正平衡点的全局渐近稳定性。

自扩散;互惠模型;存在唯一性;稳定性

美国生态学家Lotka于1921年、意大利数学家Volterra于1923年分别在研究化学反应和鱼类竞争生态系统时提出了生物数学研究中的经典模型之一——Lotka-Volterra系统。Guass和Witt在1935年将两种群的Lotka-Volterra系统一般化,得到可以反映不同种群相互作用(竞争、互惠、捕食)的系统,其中互惠模型为

这里的ai,bi,ci均为正常数。ai为相应种群的内禀增长率,b1,c2为种群内部互惠系数,b2,c1为两种群之间的竞争系数。过去的几十年中,此类经典模型被广泛研究[1]。事实上,种群在其所处环境中的分布并不是均匀的,种群也会受食物等因素影响迁入和迁出。因此,一个生态系统中的种群除了时间方向的演化外,还有空间方向上的变化,引入扩散项可以得到基于偏微分方程的生态模型。本文除了考虑物种自由扩散,还考虑种群自身密度压力导致的扩散,即具有自扩散的两种群Lotka-Volterra互惠模型

(1)

其中αi,di均为正常数,αi为种群的自然扩散系数,di为种群的自扩散系数。齐次Neumann边界条件说明在边界上不存在种群的移动。关于αi=0时高维问题的有关重要结论可以参看文献[1]和[2],具有交错扩散的问题可参看文献[3]和[4],强耦合情形的问题可参看文献[5]。 本文将重点讨论自扩散带来的影响,具体研究系统整体解的存在唯一性和正平衡点的全局渐近稳定性。

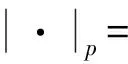
1)r≤q;

其中

C为仅与n,m,j,q,r,a有关的正常数。

下文提及的Gagliardo-Nirenberg不等式为定理1的推论。此外,还将用到文献[7]中的引理4.3,为方便阅读,重述如下:

证明正平衡解的稳定性时,为了说明解的收敛性,还将用到引理2。

引理2 设a,b为正常数,φ∈C′[a,+∞),ψ∈C′[a,+∞),ψ(t)≥0,φ有下界。如果

φ′(t)≤-bψ(t),

ψ′(t)在区间[a,+∞)有上界,则

1 解的整体存在

C∞(0,1)),

其中T是解的最大存在时间,特别地,如果解(u,v)满足

则T=+∞。

约定Aj(j=1,2,…)是只依赖于αi,ai,bi,ci的正常数,Bj(j=1,2,…)是只依赖于di,αi,ai,bi,ci的正常数。下面给出方程组(1)解的整体存在性定理。

b1c2>b2c1,

(2)

则存在仅依赖于方程组(1)中系数的正常数M,M′,t0>0,使得

max{u(x,t),v(x,t):0≤x≤1,t0≤t≤T}≤M,

从而方程组(1)存在唯一非负整数解。

证明 方程组(1)中第1个和第2个方程两边在区间[0,1]积分

(3)

(4)

式(3)和式(4)相加得

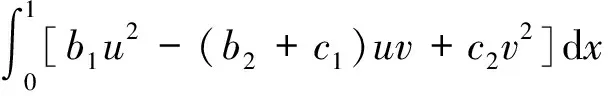
(5)

其中A0=max{a1,a2}。

由条件2)可知式(5)右端第2个被积函数正定。再由简单的代数不等式知识可得

其中

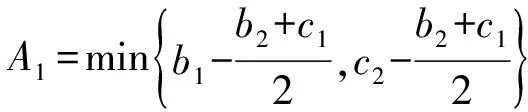
因此,存在Γ0>0,与αi,ai,bi,ci有关的正常数M0,使得

(6)

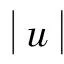
(7)

(8)

由Young不等式可得

(9)

由引理1知,存在正常数C>0,对任意ε∈(0,1)有

进而可得

(10)

由Gagliardo-Nirenberg不等式的推论

及式(6)可得

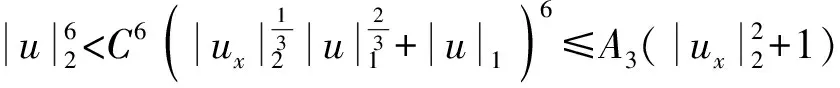
同理可得

所以有

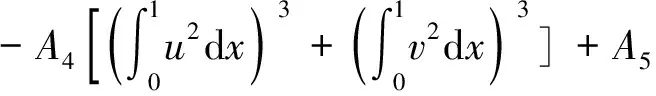
(11)

将式(9),式(10),式(11)代入式(7),式(8)得

其中d=min{d1,d2}。

考察函数

f(y)=-A7y3+A8y2+A9,

显然当A5,A6,A7,A8,A9>0时(补条件取定ε),有

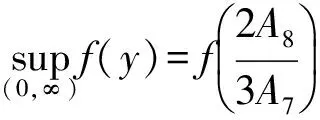
故可取

使得

因而存在正常数M1,Γ1>0,使得

(12)

(13)

(14)

由Young不等式和不等式

并结合式(6),式(12)得

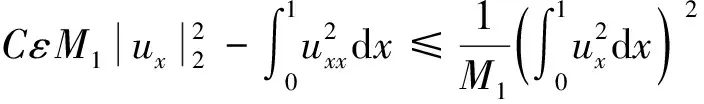
(15)

(16)

(17)

将式(15),式(16),式(17)代入式(13)得

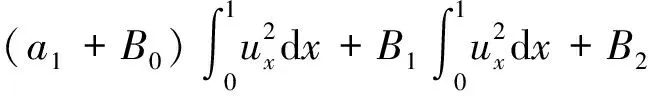
(18)

同理,式(14)可简化为

(19)

式(18)和式(19)相加得

这说明存在正数Γ3与依赖于di,αi,ai,bi,ci(i=1,2)的正常数M2,使得

(20)

综合式(6),式(12),式(20)知,存在依赖于di,αi,ai,bi,ci(i=1,2)的正常数M,t0>0,使得

因此,方程组(1)的整体解存在。进一步由Sobolev嵌入定理可知

2 正平衡点的稳定性

容易看出,当条件2)满足时,方程组(1)有正平衡解

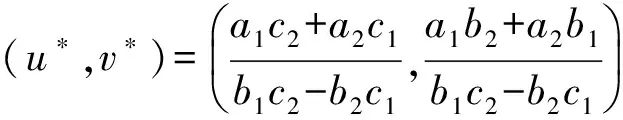
关于该平衡点的稳定性有如下结论:

4ρu*v*d1d2>(α1u*+ρα2v*)2M2,

(21)

其中

则方程组(1)的正平衡点(u*,v*)全局渐近稳定。

证明 构造Lyapunov函数

ρc2(v-v*)2]dx。

(22)

式(22)右端第2个积分号内的函数正定的充要条件为

为此,只要h(ρ)的最小值点在正半轴上,且最小值为负,这正是b1c2>b2c1的直接推论。

式(22)右端第1个积分号内的函数正定的充分条件是

4ρu*v*(d1+2α1u)(d2+2α2v)>

(α1u*v+ρα2uv*)2。

(23)

而式(21)正好是式(23)的充分条件。因此存在δ>0,使得

(24)

类似于式(22),由分部积分、Holder不等式及定理2的最大模估计可知

上有界。

因此,由引理2和式(24)可知,

t→∞,

注意到

t→∞,

即(u,v)在[0,1]上一致收敛于(u*,v*),结合H(u,v)关于t的递减性可知,(u*,v*)是全局渐近稳定的。

至此,定理3证明完毕。

[1] PAO C V. Nonlinear parabolic and elliptic equations[M]. New York: Plenum Press,1992:60-70.

[2] LOU Y,NAGYLAKI T,NI W M. On diffusion-induced blowups in a mutualistic model[J].Nonlinear Analysis: Theory, Methods and Applications,2001,45(3):329-342.

[3] DELGADO M,MONTENEGRO M,SUAREZ A. A Lotka-Volterra symbiotic model with cross-diffusion[J].Journal of Differential Equations, 2009,246(5):2131-2149.

[4] 伏升茂,高海燕.竞争—竞争—互惠交错扩散模型的整体解[J].工程数学学报,2007(3):481-486.

[5] LING Z,PEDERSEN M. Coexistence of two species in a strongly coupled cooperative model[J].Mathematical Computer Modelling An International Journal,2007,45(3-4):371-377.

[6] SHIM S A. Uniform boundedness and convergence of solutions to the systems with cross-diffusion dominated by self-diffusion[J].Nonlinear Analysis: Real World Applications,2003,4(4):65-86.

[7] SHIM S A. Uniform boundedness and convergence of solutions to cross-diffusion systems[J].Journal of Differential Equations,2002,185(1):281-305.

[8] AMANN H. Dynamic theory of quasilinear parabolic equations-I. abstract evolution equations[J].Nonlinear Anal-ysis: Theory, Methods and Applications, 1998,12(9):895-919.

[9] AMANN H. Dynamic theory of quasilinear parabolic equations-Ⅱ. reaction-diffusion[J].Differential and Integral Equations,1990,3(1):13-75.

[10] AMANN H. Dynamic theory of quasilinear parabolic equations-Ⅲ.global existence[J].Mathematische Zeitschrift,1989,202(2):219-250.

〔责任编辑： 卢 蕊〕

Existence and stability of global solutions for a cooperative model with self-diffusion

JIANG Xianghua1, CHENG Xiaoyan2, XIAO Wenbin2

(1. Danyang Normal School, Zhenjiang College ,Danyang 212310, China; 2. Maths Science Institute, Yangzhou University, Yangzhou 225002, China)

This paper deals with a two species cooperative model with self-diffusion in biomathematics.Applying energy type estimates,the exishence,uniquences of global solutions are proved.The global asymptotic stability of positive equilibrium point for this model is discussed through the constrction of Lyapunov function.

self-diffusion; cooperative model; existence and uniqueness; stability.

2016-09-24

江祥花(1972—),女,江苏丹阳人,副教授,硕士,主要从事可积系统研究; 成晓燕(1975—),女,江苏南通人,讲师,主要从事编码、密码研究; 肖文斌(1981—),男,江苏常州人,讲师,主要从事微分方程研究。

O175.26

A

1008-8148(2017)02-0075-04