凸显数学文化,彰显数学本质*
——以“等比数列的前n项和”为例
2017-06-13筅江苏省常熟市浒浦高级中学殷伟康
筅江苏省常熟市浒浦高级中学殷伟康
凸显数学文化,彰显数学本质*
——以“等比数列的前n项和”为例
筅江苏省常熟市浒浦高级中学殷伟康
等比数列中的历史文化因素促进了数列的发展,其中的人文气息和人类智慧促使人们对数学产生极大的兴趣,其内容经典,文化沉淀丰厚.等比数列的前n项和公式是高中数学的经典内容之一,常采用的推导方法是带有技巧性的“错位相减法”,由于不少教师直接“告知”求和公式及其推导方法,导致学生对此法中的两边同时乘以公比q感到难以理解,只能记住其操作步骤和结论,无法理解和领悟等比数列的前n项和公式推导方法的内涵.因此,笔者从数学文化的视角出发,结合学情,运用数学史的有效融入方式,对教材进行“二次开发”,尝试“重构式”教学方法进行教学,呈现知识的自然发生、发展过程,促进学生理解等比数列的前n项和公式推导方法的数学本质,提升学生数学素养.
一、创设情境,诱发探究
情境1一商人出售了15码的棉布,第一码售价1元,第二码售价2元,第三码售价4元,第四码售价8元,依次倍增,求总的价格.
问题1:售价依次构成等比数列,其和为S15=1+2+22+…+214.如何求和呢?
生1:S1=1=2-1,S2=3=22-1,S3=7=23-1,…,由此猜想S15=215-1.
生2:1+1=2,2+2=22,22+22=23,…,214+214=215,
逐次累加,整理得
S15=1+1+2+22+…+214-1=215-1.
生3:由生2的解法,得到启发,我认为这样求解更简捷.
S15=1+2+22+…+214+215-215=1+2(1+2+22+…+214)-215,
即S15=1+2S15-215,可以把S15看成一个未知数,解方程,求得S15=215-1.
情境2斐波纳契在《算盘书》中有这样一个问题:7个妇女去罗马,每个人牵着7匹骡子,每匹骡子负7只麻袋,每只袋子装7块面包,每块面包配7把小刀,每把刀各有7个刀鞘,问妇女、骡子、麻袋、面包、小刀、刀鞘总数是多少?
问题2:妇女、骡子、麻袋、面包、小刀、刀鞘数构成等比数列,其和为S6=7+72+73+74+75+76.怎么求和呢?(学生仿照生3的解法,从方程角度进行求解.)
问题3:等比数列的前n项和Sn=a1+a2+…+an=a1+ a1q+…+a1qn-1又如何计算?
设计意图:以16世纪数学家巴克著作中的棉布问题和斐波纳契著的《算盘书》中的经典问题作为情境引入,创设数学文化情景,使原本枯燥、抽象的数学知识变得生动有趣,激发学生探究新知的欲望.让学生在尝试探究中,体验数学的应用价值.
二、探索发现,建构数学
即Sn=a1+qSn-a1qn,解得
生5:上式要满足q≠1,若q=1,则Sn=na1.
设计意图:生3的解法是构造S15为未知元的方程,利用方程思想求解S15.引导学生从特殊到一般,运用类比的方法,将方程思想迁移到“等比数列的前n项和”求和的过程中.
师:很好!考虑问题要体现严谨性.如果不添加项,能否直接求和呢?
生6:Sn=a1+a1q+a1q2+…+a1qn-1
=a1+q(a1+a1q++…+a1qn-2)
=a1+qSn-1,
师:从后面(n-1)项中直接提取公因式q,得到新的递推式,其中Sn-1怎么处理呢?
生6:又当n≥2时,Sn=Sn-1+an,将Sn-1=Sn-an代入递推式,
生4:Sn=a1+a1q+…+a1qn-1+a1qn-a1qn
=a1+q(a1+a1q+…+a1qn-1)-a1qn,
*本文系江苏省教育科学“十二五”重点资助课题:构建数学文化课堂的教学实践研究(课题批准号B-a/2013/02/069)研究成果之一.Sn=a1+q(Sn-an),
设计意图:这种提取因式法推导等比数列的前n项和公式的方法是古代埃及人最先提出的,简洁明了,赏心悦目.其实生3的解法中已经隐含有“提取因式法”,所以运用提取因式法进行求和,水到渠成.难点是如何将Sn-1进行转化,若从Sn的定义入手,则能发现两者之间的关系.
师:如果从等比数列的定义出发,结合合分比定律,能否推导等比数列的前n项和公式呢?

设计意图:古希腊数学家欧几里得在《几何原本》中首次提出运用等比定律法推导等比数列的前n项和公式,

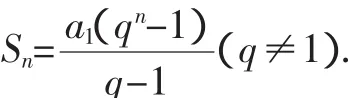
他还对推导方法进行改进:
由于此法基于等比数列的定义和学生熟知的等比定律法,因而此法显得更为自然.
师:欧几里得与生7的解法不完全相同,但是异曲同工.
生8:还应该考虑分母不为零,Sn≠0.
师:运用方程思想、提取因式法和等比定律法得到了求和公式,还有没有其他方法呢?
生9:Sn=a1+a1q+a1q2+…+a1qn-1,
Sn-a1=a1q+a1q2+…+a1qn-1,
Sn-a1qn-1=a1+a1q+…+a1qn-2,
Sn-a1=q(Sn-a1qn-1)
设计意图:这种推导方法称为掐头去尾法.法国数学家拉克洛瓦(1765~1843)采用此法进行推导.
师:能否类比等差数列的前n项和公式的推导方法进行推导呢?
生10:运用倒序相加法目的是构造相同和的形式,但对于等比数列,好像不奏效.
师:倒序相加法的本质是什么?
生11:构造一个新的式子(方程),通过两式相加(线性运算),将不同数的数列求和转化为相同数的数列求和,即常数列求和.
师:从方程角度,使用倒序相加法以达到消除干拢项的目的,根据等比数列的性质,无论怎样求和好像都没办法消掉中间的项,那怎么办呢?
生12:构造一个等式(方程)与原来的等式(方程)作差.
师:如何构造这个等式呢?
生12:只要两个等式(方程)中出现大量相同的项,就可以作差求和.
生12:Sn=a1+a1q+a1q2+…+a1qn-1,①
观察上式,若方程两边同时乘以公比q,则qSn这个和式与Sn的和式中,就会出现大量相同的项.
qSn=a1q+a1q2+…+a1qn-1+a1qn,②
由①-②,得(1-q)Sn=a1-a1qn
设计意图:这种推导方法称为错位相减法,欧拉(1707~1783)首次采用此法进行推导.在引导学生推导等比数列的前n项和公式的过程中,通过类比等差数列的前n项和公式的推导方法,让学生明确消项是求和的基本方法,然后再探求消项的方法,这样可以突破教学难点.对求和的基本方法的数学本质的认识越深刻,对数学方法本身的理解就会越自然.
师:在数学推理中,若正面考虑较难时,则往往从它的反面进行思考.能否仿照上面的推导思路,从其他角度进行推导呢?
生13:乘法的逆运算是除法,方程①两边同时除以公比q,也可以求和.
生14:老师,我发现方程①两边同时乘以“-q”也可以求和.
师:很好!体现了“正难则反”的思想,从逆向思维的角度进行推导.能否根据等差数列通项公式的推导方法(累加法)进行推导呢?
生15:关键要构造相邻两项的差式.
师:如何构造呢?学生经过反复尝试,有所发现.
生16:a1-a2=(1-q)a1,a2-a3=(1-q)a2,…,an-an+1=(1-q)an,
以上n个等式左右分别相加,得a1-an+1=(1-q)Sn,
以上n个等式左右分别相加,也可以得到Sn=
师:两位同学运用累加法进行求和,思维独特,很有创意,值得欣赏和借鉴.
设计意图:通过启发,引导学生从逆向思维的角度、类比等差数列通项公式的推导方法进行探究求和公式.
三、文化引领,彰显本质
探索数学的本质是数学教学的真谛,只有揭示数学本质才是数学教学的灵魂所在.但是不少教师急功近利,不愿在概念建构、公式的推导过程中花力气,仅仅停留在教材所呈现的推导形式上,宁愿不惜时间用在例题讲解和习题训练上,导致学生对概念、公式的理解是肤浅的,对概念、公式所蕴含的数学思想方法知之甚少,更无法理解和领悟数学的本质.
1.回归自然,领悟本质
在数学教学过程中应充分揭示数学知识产生、发展的过程,同时强调数学公式的形成应该是自然的、符合学生的认知规律的.通过挖掘史料,创设“巴克著作中的棉布问题和斐波纳契著的《算盘书》中的经典问题”史料情境,诱发学生探究等比数列的前n项和公式,让学生经历数学公式的探究过程,从而理解公式,掌握推导方法,领悟本质.这样的教学,符合学生的认知规律,求和公式的产生让学生感到比较自然,并能使学生认识到求和公式背后所蕴含的丰富而鲜活的内容与思维方法,从而让学生感到枯燥乏味的数学其实本身是生动活泼的、趣味盎然的.
2.抓住本质,领悟思想
数学文化的核心是在数学产生、发展的历史进程中,逐步沉淀下来的数学思考、数学观念、数学品质等.数学知识是数学家思维活动的成果,数学家的思维方法和思维过程是数学文化中宝贵的财富.教师要从数学文化的视角,挖掘数学知识形成过程中数学家思维活动方式,利用数学家的思考方式和方法来突破思维瓶颈.对教材进行再创造,融入数学史料,通过创设有效的问题链,激发学生参与探究,引导学生从方程、等比定理等角度出发,模仿欧几里得、拉克洛瓦的推导方法的过程,探究求和公式.让学生在探究中,经历获得等比数列的前n项和公式的思维活动经验,感悟其所蕴含的数学思想方法.笔者认为:对于错位相减法的突破要数学思想层面上下足工夫.“能否类比等差数列的前n项和公式的推导方法进行推导呢?”引导学生从倒序相加法的本质是转化与化归思想出发,认识到“消项”是求和的基本方法,类比推导出“错位相减法”,学生还从逆向思维的角度进行探究,提出了“方程①两边同时除以公比q或乘以-q也可以求和”的想法,这样有利于促进学生对错位相减法的本质认识.学生经历观察、分析、类比、猜想、抽象、推广等一系列思维活动,学会数学地思考,从多元的角度分析问题、理解问题,探究等比数列的前n项和公式,揭示数学方法的本质,逐步领悟方程思想、错位相减法、正难则反等数学思想方法的内涵.让学生在尝试探究成功的欢愉之中,感悟公式的推导方法之美,品味数学的韵味,体验数学文化的魅力.
3.展示思维,培养素养
章建跃博士认为:没有“过程”的教学把“思维的体操”降格为“刺激—反应”训练,是教育功利化在数学教学中的集中体现.在等比数列的前n项和公式教学中,教师普通采用教材上的错位相减法进行推导求和公式,强调方法的操作步骤,而忽视求和公式的形成过程的探究,以及对错位相减法的本质的认识.其实数学概念的建构、公式的推导,总是在一定文化下的某一种思考,都有其深刻的背景.在教学中,注重还原、再现数学概念的建构、等比数列的前n项和公式的推导的思维过程,进行科学地合情合理地引导,诱发学生探究,并创设交流时机,展示学生的思维过程.学生在问题情境中尝试运用方程思想进行求和,类比方程思想,探究等比数列的前n项和公式,并在求和过程中学生自行不断修改、完善.引导学生模仿数学家的思维活动(等比定律法、掐头去尾法和错位相减法)进行求和,尤其学生从逆向思维角度提出了对错位相减法的改进方法,增进了对错位相减法的本质的理解,这样错位相减法就会在学生脑海中根深蒂固,从而发展学生的数学素养.学生运用累加法进行探究求和公式,并提出自己的认识,这种能够数学地表达属于自己的观点,有利于培养学生的数学核心素养.在这样的探究和思维活动中,学生会不知不觉地获得基本数学素养,学会用数学的眼光去审视现实问题、思考问题,获得研究数学问题的一些基本方法和积累数学活动的基本经验.
1.吴现荣,宋军.HPM视角下的等比数列前n项和公式教学[J].数学通报,2016(7).
2.张勤,李德安.数学史融入中学数学教学初探——以“等比数列前n项和公式推导”为例[J].数学通讯,2016(2).
3.周龙虎.“等比数列前n项和”教学思考[J].中国数学教育,2015(12).
