非线性渗流连续模型力学原理及适用性
2017-06-12凌浩川周海燕杨正明王学武
凌浩川,周海燕,胡 勇,杨正明,王学武
(1.中海石油(中国)有限公司 天津分公司渤海石油研究院,天津 300452;2.中国石油勘探开发研究院 廊坊分院,河北 廊坊 065007)
非线性渗流连续模型力学原理及适用性
凌浩川1,周海燕1,胡 勇1,杨正明2,王学武2
(1.中海石油(中国)有限公司 天津分公司渤海石油研究院,天津 300452;2.中国石油勘探开发研究院 廊坊分院,河北 廊坊 065007)
从低渗透油藏产生非线性渗流的微观机理出发来推导该模型,并进一步分析得出当静态下边界层的厚度大于孔隙半径的1/4时,该模型不再适用。微管渗流实验表明:当渗流孔隙半径为1 μm时,静态下的边界层厚度超过0.25 μm,占孔隙半径的25%以上,因此非线性渗流连续模型适用于孔隙半径大于1 μm的储层,当孔隙半径小于1 μm时,不再适用。
低渗透油藏;非线性渗流;边界层厚度;致密油藏界限
低渗透油藏非线性渗流研究一直以来是比较受争议的一个问题。截至目前非线性渗流渗流机理的解释大致可以分为两种理论:第一就是边界层理论[1-6],第二就是考虑屈服应力的渗流模型[7-9]。杨清立在其博士论文里提出的低渗透油藏非线性连续模型是根据大量低渗岩心实验数据及其曲线形态分析总结出来的渗流规律。非线性渗流连续模型在低渗透油藏研究中起到了重要的作用,但是该渗流规律能否从已有的渗流理论推导而来,以及具有什么样的局限性却暂无更加深入的研究。从边界层理论出发推导该模型,并提出非线性渗流连续模型的使用也具有一定的局限性。通过微管渗流实验结果说明:当储层的孔隙半径小于1 μm时该模型不再适用。该研究对划分低渗和致密油藏的界限具有一定的指导意义。
1 模型建立
渗流流体是渗流环境中的流体,它包括体相流体和边界流体两部分(如图1所示)。体相流体是指其性质不受界面现象影响的流体,它分布在多孔介质孔道的中轴部位;边界流体是指其性质受界面现象影响的流体,它紧靠在孔道壁上形成一个边界层[1]。
边界流体靠近孔道壁,由于固液表面分子间作用力、分子间的极性等影响,要使其流动很难,需要在一定压力梯度下才能参与流动。为了定量描述流体通过孔道的面积随压力梯度变化的大小,引入边界层厚度变化率的概念。
(1)
其中:h为边界层厚度;p为压力梯度;ch为边界层厚度变化率。
一般认为边界层厚度变化率的大小与渗流流体以及岩石孔壁的性质有关系,对于同一种渗流流体在同样大小的毛细管中ch为常数。假设半径为r的毛细管中静态下边界层厚度为h0,则有:
h=h0e-ch|p|
(2)
单根毛细管流量公式为[5]:
(3)
(2)代入(3)并化简得:
(4)
假设岩心由n根等半径的毛细管束组成,则总流量整块岩心的流量为:
(5)
对于毛细管岩石模型有:

(6)
联立(5)(6)可以得到毛细管岩石模型的流速计算公式:
(7)
式(7)泰勒展开,并且忽略高次项可得:
(8)
根据ex≈1+x,上式可以化简为:
(9)
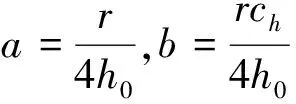
公式(9)即为杨清立博士通过大量低渗岩心实验数据总结出的非线性渗流连续模型。
符号说明:r为孔隙半径,μm;h0为静态下边界层厚度,μm;p为压力梯度,MPa·m-1;λ为启动压力梯度,MPa·m-1;ch为边界层厚度变化率,MPa-1;q为单根毛细管流量,μm;Q为岩心流量,μm;μ为流体黏度,mPa·s;k为渗透率,mD;ø为孔隙度。
2 适用性分析
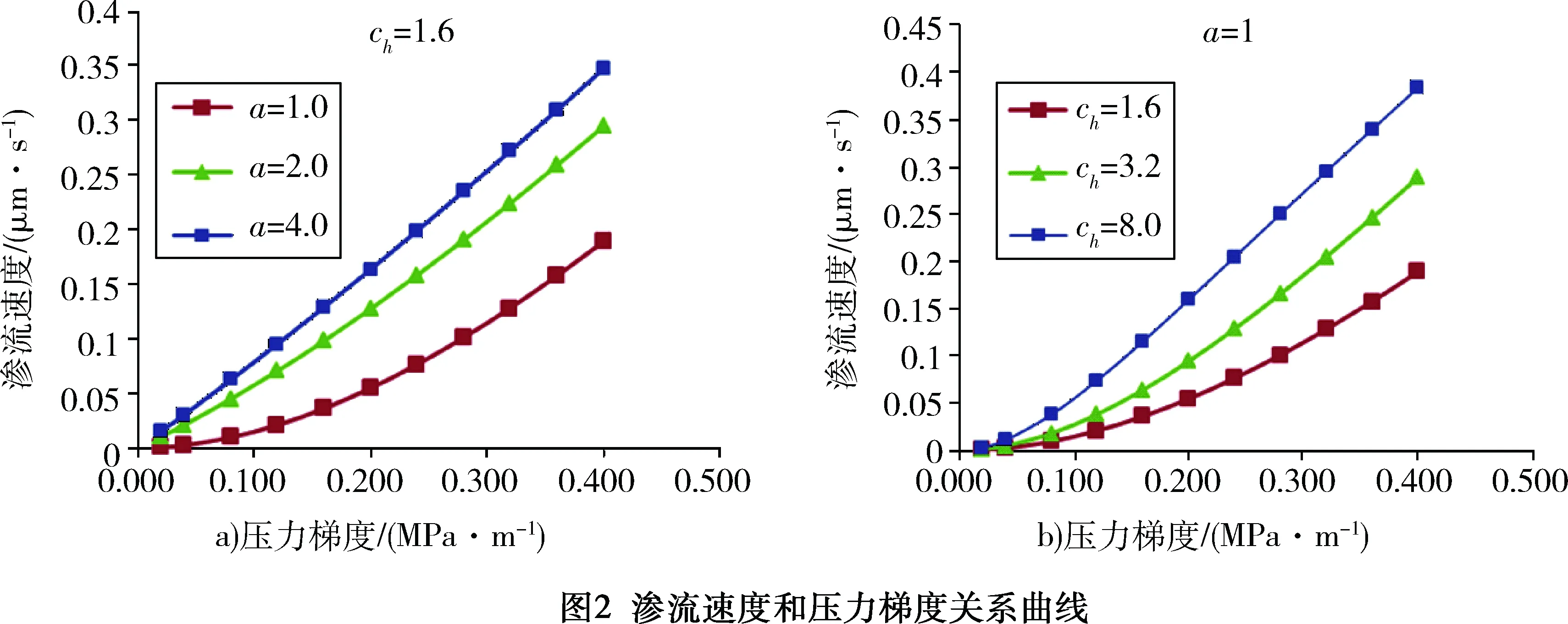
杨清立博士通过大量低渗岩心实验数据总结出的非线性渗流规律是具有渗流力学理论依据的。其论文中提到的参数a为影响非线性渗流凹形曲线段的影响因子[2],其实具有非常清楚的物理意义:参数a反映的是渗流孔隙半径和静态下边界层厚度的相对大小;a越小,则静态下边界层厚度h0越大,其非线性越强。参数b和边界层厚度变化率ch成正比;ch越小,则边界层随压力梯度的变化越缓慢,从而非线性越强(如图2所示)。


3 微管渗流实验
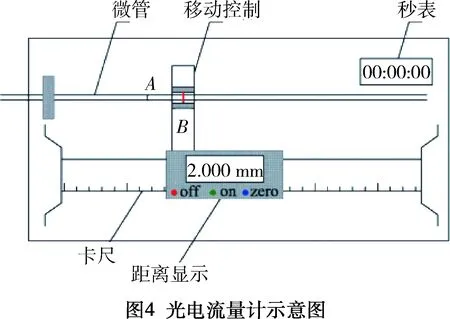
实验选用了全球最先进的微毛细管制造公司PolyMicro公司的熔融石英毛细管系列产品。采用光电流量计(如图4所示)来记录流速大小,采用去离子水作为流动介质,采用恒压法分别测量管径为 2.5μm和1.0μm下压力梯度和流量的关系曲线。利用式(3)计算边界层厚度随压力梯度的变化关系。通过指数拟合可以获得边界层厚度随压力梯度变化的曲线(如图5所示)。结果表明:当渗流孔隙半径为2.5μm时,静态下的边界层厚度达到0.326μm,占孔隙半径的13%,当渗流孔隙半径为1μm时,静态下的边界层厚度达到0.252μm,占孔隙半径的25%以上。

4 结论和认识
1)从边界层理论出发推导了非线性连续模型,结果表明该模型参数a的本质反映的是渗流孔隙半径和静态下边界层厚度的相对大小,a越小,则静态下边界层厚度h0越大,其非线性越强。
2)从模型本身出发,结合推导过程剖析了非线性连续模型的适用性,结果表明当静态下边界层的厚度大于孔隙半径的1/4时,非线性渗流连续模型不再适用。
3)开展微管渗流实验来研究不同渗流孔隙半径下的边界层厚度,实验结果表明:当渗流孔隙半径为1 μm时,静态下的边界层厚度达到0.252 μm,占孔隙半径的25%以上,因此非线性渗流连续模型适用于孔隙半径大于1 μm的储层。
[1] 黄延章.低渗透油层渗流机理[M].北京:石油工业出版社,1998.
[2] 杨清立,杨正明,王一飞,等. 特低渗透油藏渗流理论研究[J].钻采工艺,2007(6):52-54.
[3] 姚约东,葛家理,魏俊之. 低渗透油层渗流规律的研究[J].石油勘探与开发,2001(4):73-75.
[4] 时宇,杨正明,杨雯昱. 低渗储层非线性相渗规律研究[J].西南石油大学学报(自然科学版),2011(1):78-82.
[5] 张代燕,王子强,王殿生,等. 低渗透油藏最小启动压力梯度实验研究[J].新疆地质,2011(1):106-109.
[6] 刘卫东,刘吉,孙灵辉,等. 流体边界层对低渗透油藏渗流特征的影响[J].科技导报,2011(22):42-44.
[7] 杨仁锋,姜瑞忠,孙君书,等. 低渗透油藏非线性微观渗流机理[J].油气地质与采收率,2011(2):90-93.
[8] 胡华君,马铭勖,李光明. 低渗透毛管束单相渗流模型的建立[J].重庆科技学院学报(自然科学版),2011(3):93-95.
[9] 李中锋,何顺利. 低渗透储层原油边界层对渗流规律的影响[J].大庆石油地质与开发,2005(2):57-59.
简 讯
教育部专家来我校进行思政课建设调研。根据教育部2017年高校思政课教学质量年专项工作总体方案要求,5月26日,教育部思政教指委高职高专分教指委主任、北京联合大学党委书记韩宪州研究员一行两人到我校进行思政课建设调研,校党委书记王纪安全程陪同。专家听取了我校思政课建设情况汇报,介绍了教育部关于加强思政课建设的相关信息,随机听取了教师课堂授课,与任课教师深入交换了意见,并随堂对学生进行了访谈。专家对我校思政课教学给予了充分肯定,也就进一步加强思政课建设提出了建议。专家还参观了校史馆,实地考察了校园文化建设情况。
Mechanism and Applicability Analysis of ContinuousModel of Nonlinear Flow
LING Hao-chuan1, ZHOU Hai-yan1, HU Yong1,YANG Zheng-ming2, WANG Xue-wu2
(1.Bohai Oilfield Research Institute, CNOOC Ltd., Tianjin, Tianjin 300452, China; 2.Langfang Research Institute of Exploration and Development, PetroChina, Langfang 065007, Hebei, China)
In this paper, continuous model of nonlinear flow is derived based on the microscopic mechanism of low permeability reservoirs. The results show that the model is no longer applicable when the thickness of boundary layer is over a quarter of formation pore radius. The microtubules seepage experiments show that when the pore radius is less than 1 μm, the thickness of the boundary layer can reach over 0.25 μm, which is over a quarter of pore radius. Hence continuous model of nonlinear flow can be used only when the pore radius is larger than 1 μm, and the model would be out of use when the pore radius is less than 1 μm.
low permeability reservoirs; nonlinear flow; thickness of boundary layer; limit of tight reservoirs
2016-10-10
凌浩川(1987-),男,湖南岳阳人,从事油藏工程和数值模拟研究工作,E-mail:xuanmuzixu@163.com。
TE31
A
1008-9446(2017)03-0013-04
