低秩矩阵恢复的近似迭代再加权算法
2017-06-12王鹏胡洁仪陈剑波
王鹏,胡洁仪,陈剑波
(五邑大学 数学与计算科学学院,广东 江门 529020)
低秩矩阵恢复的近似迭代再加权算法
王鹏,胡洁仪,陈剑波
(五邑大学 数学与计算科学学院,广东 江门 529020)
低秩矩阵恢复问题常常正则化为非凸非光滑的最优化问题,并用迭代再加权算法求解.本文借助迹算子的次梯度提出了一种近似算法,避免了求解线性方程组而直接求解.
低秩矩阵恢复;迭代再加权;SVD分解
低秩矩阵恢复是近年来计算数学和信息科学中的一个热门研究领域,相关成果广泛应用于图像处理、子空间分割、协同滤波等领域.低秩矩阵恢复问题一般表述为

本文将上述问题正则化为以下非凸非光滑的优化问题:

1 预备知识
为了求解式(1),首先引入它的一种光滑近似形式[1]929:
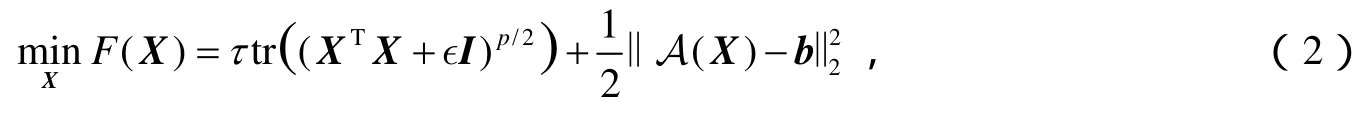
引理1[4]设,其中函数是正交不变函数,是一个绝对对称函数,则在是次可微的,并且
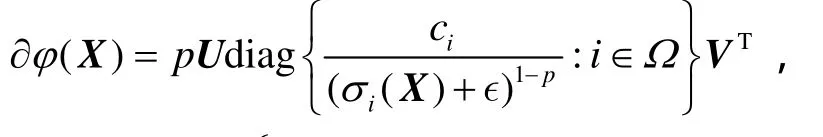

由式(3)并结合迹算子的凹凸性[5]可知为凹函数,则为凸函数.由次梯度的定义得:



关于光滑函数的李普希兹连续有如下引理:
引理2[6]设是李普希兹连续可微函数,李普希兹常数为L(f),则对于任意的可得:

2 主要结果
本部分将给出求解最优化问题(2)的近似迭代再加权算法,并结合式(6)和(7)给出Xk+1的迭代格式.

我们得到的低秩矩阵恢复的近似迭代再加权算法如下:
4)更新权重Wk+1,,其中,
5)输出低秩矩阵kX.
对于低秩矩阵恢复问题,现有算法多将原非凸问题正则化为凸优化问题,然而,非凸正则化要比凸正则化效果更好.本文将迭代再加权算法用于低秩恢复问题求解,借助迹算子的次梯度避免了求解线性方程组而直接求解.
[1] LAI Mingjun, XU Yangyang, YIN Wotao.Improved iteratively reweighted least squares for unconstrained smoothed lqminimization [J].SIAM Journal on Numerical Analysis, 2013, 51(2): 927-957.
[2] KONISHI K, URUMA K, TAKAHASHI T, et al.Iterative partial matrix shrinkage algorithm for matrix rank minimization [J].Signal Processing, 2014, 100: 124–131.
[3] MOHAN K, FAZEL M.Iterative reweighted algorithms for matrix rank minimization [J].Journal of Machine Learning Research, 2012, 13(1): 3441-3473.
[4] LI Yufan, ZHANG Yanjiao, HUANG Zhenghai.A reweighted nuclear norm minimization algorithm for low rank matrix recovery [J].Journal of Computational & Applied Mathematics, 2014, 263: 338-350.
[5] BEKJAN T N.On joint convexity of trace functions [J].Linear Algebra & Its Applications, 2004, 390: 321-327.
[6] TOH K C, YUN S W.An accelerated proximal gradient algorithm for nuclear norm regularized least squares problems [J].Pacific Journal of Optimization, 2010, 6(3): 615-640.
[责任编辑:熊玉涛]
Proximal Iteratively Reweighted Algorithm for Low Rank Matrix Recovery
WANG Peng, HU Jie-yi, CHEN Jian-bo
(School of Mathematics and Computational Science, Wuyi University, Jiangmen 529020, China)
Low rank matrix recovery is often regularized into a non-convex and non-smooth optimization problem, which can be solved with iteratively reweighted algorithms.This paper proposes a proximal algorithm with the subgradient of trace operators, and consequently the problem can be solved directly and the system of linear equations can be disposed of.
low rank matrix recovery; iteratively reweighted algorithms; singular value decomposition
O189.1
A
1006-7302(2017)02-0006-03
2017-02-26
五邑大学青年基金资助项目(2015ZK09);广东省大学生创新创业项目(1134912031).广东省高等教育教学改革项目(30527003,JG2014010);广东省普通高校特色创新类项目(2016GXJK161).
王鹏(1980—),男,广东江门人,讲师,硕士,研究方向矩阵优化计算、数字图像处理与分析.
