穷思竭虑疑无路 柳暗花明又一题*
——例说导数零点“不可求”的解题策略
2017-06-12周超艳宁波市惠贞书院浙江宁波315016
●周超艳 (宁波市惠贞书院 浙江宁波 315016)
穷思竭虑疑无路 柳暗花明又一题*
——例说导数零点“不可求”的解题策略
●周超艳 (宁波市惠贞书院 浙江宁波 315016)
文章通过分析导数零点和符号,研究函数单调性、极值、最值等问题.当导数零点比较难求时,很难借助导数研究函数的性质.文章通过例题介绍了猜根、再次求导、数形结合等8种解题策略,从而使导数零点“不可求”问题迎刃而解.
导数;零点;策略
导数是研究函数单调性、极值和最值的重要工具,也是浙江省新增的数学高考必考内容之一.笔者通过分析导数的零点,确定导数的符号,研究原函数的单调性,从而解决与函数单调性相关的极值、最值、零点等问题.但也不可避免地遇到导函数的零点无法通过解方程求得的情形,这就大大增加了解题难度.笔者就导数零点“不可求”问题,介绍若干解题策略,供大家探讨.
1 猜根策略


评注g′(x)=0是一个超越方程,根据式子特征进行猜根可得x=1.为了防止漏根,可以对导函数或导函数的部分式子进行单调性分析,说明其充要性.
2 再次求导策略




g′(x)=x-lnx-1(其中x>1).

评注 该题导函数的零点问题仍是一个超越方程问题,虽然可以猜根得x=1,但需先对g′(x)进行再次求导,进一步确定其单调性,从而说明g′(x)的符号及证明x=1是g′(x)的唯一零点,最后求得g(x)的最值.
3 数形结合策略
例3 题同例2
分析 该题已用“再次求导策略”得以求解.事实上,该导数的零点问题也可以借助数形结合进行解决.

图1

lnx=x-1,
易知y=lnx与y=x-1相切于点(1,0),如图1,从而
g′(x)=x-lnx-1>0(其中x>1),
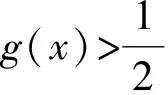
评注 数形结合是求解超越方程的常用方法之一.该题通过分析直线与曲线的位置关系求得g′(x)的零点,也说明了当x>1时导函数的符号,从而确定了f(x)的单调性.
4 零点存在性定理策略
(2017年浙江省数学高考模拟试题第20题)
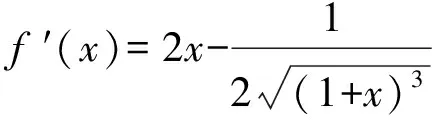
评注 虽然f′(x)的单调性易确定,但无法求得其零点.通过零点存在性定理说明f′(x)在[0,1]上的零点情况,从而确定f(x)的单调性,求得f(x)的最大值.
5 代入转化策略
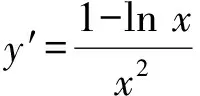
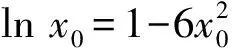


即证

设h(x)=6x2+lnx-1,则h(x)在(0,+∞)上单调递增,又
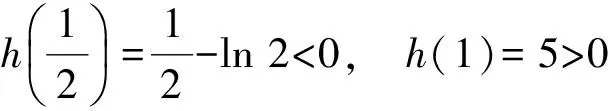

6 代入消参(元)策略
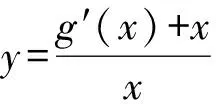

g′(x)=3x2-x+c,
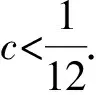


评注 通过代入消参,减少了变量,简化了函数.该题虽然可以通过求根公式解得导函数的零点,但会大大增加求解h(m)取值范围的运算量.
7 部分代换策略
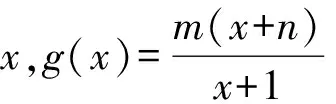

(ln 2a-lnx)ax+lnx-ln 2a≤0.
设h(x)=(aln 2a)x-axlnx+lnx-ln 2a,由h(x)≤0对所有正数恒成立可得a>0,且h(x)max≤0.又
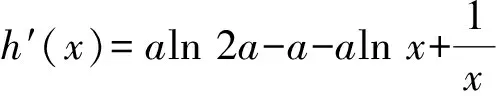
且

于是h″(x)在定义域上单调递减.当x→0时,h′(x)→+∞;当x→+∞时,h′(x)→-∞,因此存在正实数x0使得h′(x0)=0,即

因为h(x)在(0,x0)上单调递增,在(x0,+∞)上单调递减,所以
h(x)max=(aln 2a)x0-ax0lnx0+lnx0-ln 2a,




即
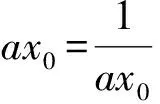

点评 虽然无法解得该导函数的零点,也不能用策略5、策略6把x0或a进行代换,但通过部分代换,把lnx0转化为关于x0的分式,也能简化目标式,达到转化的目的.
8 放缩策略
例8 已知函数f(x)=x3+3ax2+3x+1,若x∈[2,+∞)时,f(x)≥0,求a的取值范围.


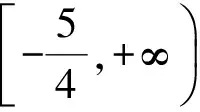
评注 先通过必要条件缩小参数a的取值范围,再对导函数进行放缩,化动为静,从而确定f(x)的单调性.
综上可知,求解导函数的零点问题本质就是求解函数的零点问题,解方程、零点存在性定理、数形结合是解决该类问题的通法.对于部分超越方程或者含参方程,当通法无法解决时,可以通过代换、设而不求、巧妙转化,亦或是巧搭桥梁、合理放缩,从而使“穷思竭虑疑无路”的导数题得以“柳暗花明”.
2017-02-14;
2017-03-16
周超艳(1987-),女,浙江宁波人,中学二级教师.研究方向:数学教育.
O122.1
A
1003-6407(2017)06-23-03
