Isight在博弈多目标优化中的应用

叶文海，陈 亮，李廖平

(福州大学机械工程及自动化学院，福建 福州 350116)



Isight在博弈多目标优化中的应用

叶文海，陈 亮，李廖平

(福州大学机械工程及自动化学院，福建 福州 350116)

复杂多目标优化设计中常遇到性能目标与设计变量之间不具有显式的函数关系式，难以直接运用传统优化方法进行设计求解，且存在多个性能目标相互耦合，设计周期长等问题. 针对这些问题，提出一种Isight的博弈多目标优化设计方法，在Isight优化平台下集成Solidworks软件和Ansys软件进行建模与分析，运用博弈论思想分别建立合作博弈框架和非合作博弈框架，用遗传算法对模型进行求解获得优化解，并以悬臂梁多目标优化设计进行示例说明.

Isight平台； 博弈论； 多目标优化设计； 悬臂梁

0 引言

工程应用中产品多目标优化设计案例总是希望设计对象的各性能目标在确定的边界约束下均尽可能最优[1]. 但设计对象的各个性能目标并非相互独立，而是相互联系、 相互耦合的，需要应用多目标优化方法进行综合求解. 对于多目标决策问题的求解，传统方法是将多个设计目标使用一定的转换方法变换为单个目标[2-4]. 该方法应用简单，但原问题方法需用明确的数学表达式来描述，并对不同量纲的多个目标进行强行耦合，且具体耦合措施需要先验经验，致其难以被广泛认同. 对于实际情况中无法建立常规意义优化数学模型的产品设计，则不能使用传统多目标优化方法来解决[5-6]. 而在工程实际中这类问题往往更常见，因此对这种问题的处理方法进行研究更具有实用价值.

针对以上问题，提出一种基于Isight的博弈多目标优化方法，在Isight优化平台下建立博弈模型框架并集成Solidworks和Ansys求解多目标优化设计问题. 博弈论适用于研究决策者彼此相互作用时的决策及协调问题，为分析两个及两个以上理性参与者的决策问题提供了一种有效的解决办法[7]. 利用Isight将三维建模软件、 分析处理软件和优化软件集成起来，运用博弈论方法来解决那些常规优化方法难于处理的多目标优化设计问题.

1 博弈模型

一个博弈问题的构成涉及博弈参与者、 各方收益、 各方可支配的策略集三个主要内容. 与多目标优化问题中的相关要素相对应，优化问题中的各目标函数即博弈问题的参与者，各目标函数值即博弈方的收益，而各优化目标所选择的设计变量可行域即为博弈方可选择的策略集.

1.1 合作博弈[8]

众多的博弈方结盟，整体收益与各博弈方收益息息相关的，彼此间信息互通，同时决策，各方收益的提高以不导致整体收益的降低为前提，强制执行具有约束力的契约. 合作博弈各方相互协商，进行合作，彼此妥协与退让，达成共识，既使得自身收益满意，又使得集体收益增加. 多目标设计过程中，每个设计目标都是博弈中的一方，各设计目标之间进行合作协商，制定合约，并按照约定强制执行决策.

由于各设计目标之间可能相差几个数量级，为了避免数量级相差太大而对设计结果产生影响，需要对各个设计目标进行归一化处理，将各个博弈方置于同一水平，来消除各目标数量级不同的影响，建立合作博弈的数学模型为：

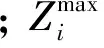
1.2 非合作博弈[9]

各博弈方信息互不共享，决策互不协商，不能够达成具有约束力的协议，收益互有影响和冲突. 通过理性竞争方式，各方在收益互相矛盾的背景下以自身收益最大化为向导进行策略抉择. 在设计过程中，各博弈方需要通过对其他博弈方选择的策略进行估计来作出对自己有利的决策，直到达成收益均衡. 非合作博弈各方既希望自身收益最优，同时也需对其他方收益做出妥协，从而协调各方收益分配，缓解彼此间的收益冲突. 多目标优化设计博弈中，各设计目标都以自身目标函数值最小化为向导，决定满意的设计变量集. 在互相知晓各设计目标也谋求自身目标函数值最小化的条件下，对其所选择设计变量集的域进行估计，综合考虑后，对自身所采用的设计变量集作出调整.

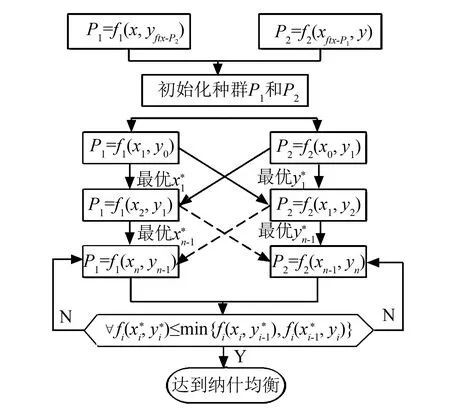
图1 非合作博弈求解流程Fig.1 Solution process of non-cooperative game

为此建立基于遗传算法的求解模型，采用模糊聚类方法对多目标优化设计变量集进行归类，获得分属于各博弈方的策略集，每个博弈方被分配一个种群或一个目标函数进行优化，各方只可以修改分配给他的变量集. 在每个时间点后，如一代后，博弈方和其他博弈方交换他们的最优值，直到没有博弈方可以通过改变其最佳策略来提高他的收益或目标值时为止，此时收敛于一个纳什均衡. 详细求解流程如图1所示，目标函数为minf(x,y). 设计变量x由博弈方P1控制，y由博弈方P2控制. 博弈方P1通过改变x使minf(x,y*)，其中，y*是来自博弈方P2的信息，是确定的. 同样，博弈方P2通过改变y使minf(x*,y)，其中，x*是来自博弈方P1的信息，也是确定的. 当P1和P2都不能提高其目标函数minf(x,y*)和minf(x*,y)的收益时，即minf(x*,y*)≤minf(x,y*)和minf(x*,y)时, 达到纳什均衡.

2 基于Isight的多目标博弈框架

根据多个目标之间的相互关系，存在合作关系的目标进行合作博弈求解，存在竞争关系的目标进行非合作博弈求解，分别建立基于Isight的合作博弈框架和非合作博弈框架，如图2和图3所示. 合作博弈框架由一个优化器、 两个Simcode程序集成组件和一个Calculator计算器组件构成，其中两个Simcode程序集成组件分别用于集成Solidworks软件与Ansys软件. 非合作博弈框架有一个循环器、 多个优化器及其内部各自的两个Simcode程序集成组件和外部的两个Simcode程序集成组件构成，其中优化器外部的两个Simcode程序集成组件用于重新计算每一次非合作迭代后的目标结果. 箭头方向表示计算流程的顺序关系，非合作博弈框架中的多个优化器之间属于并行关系.

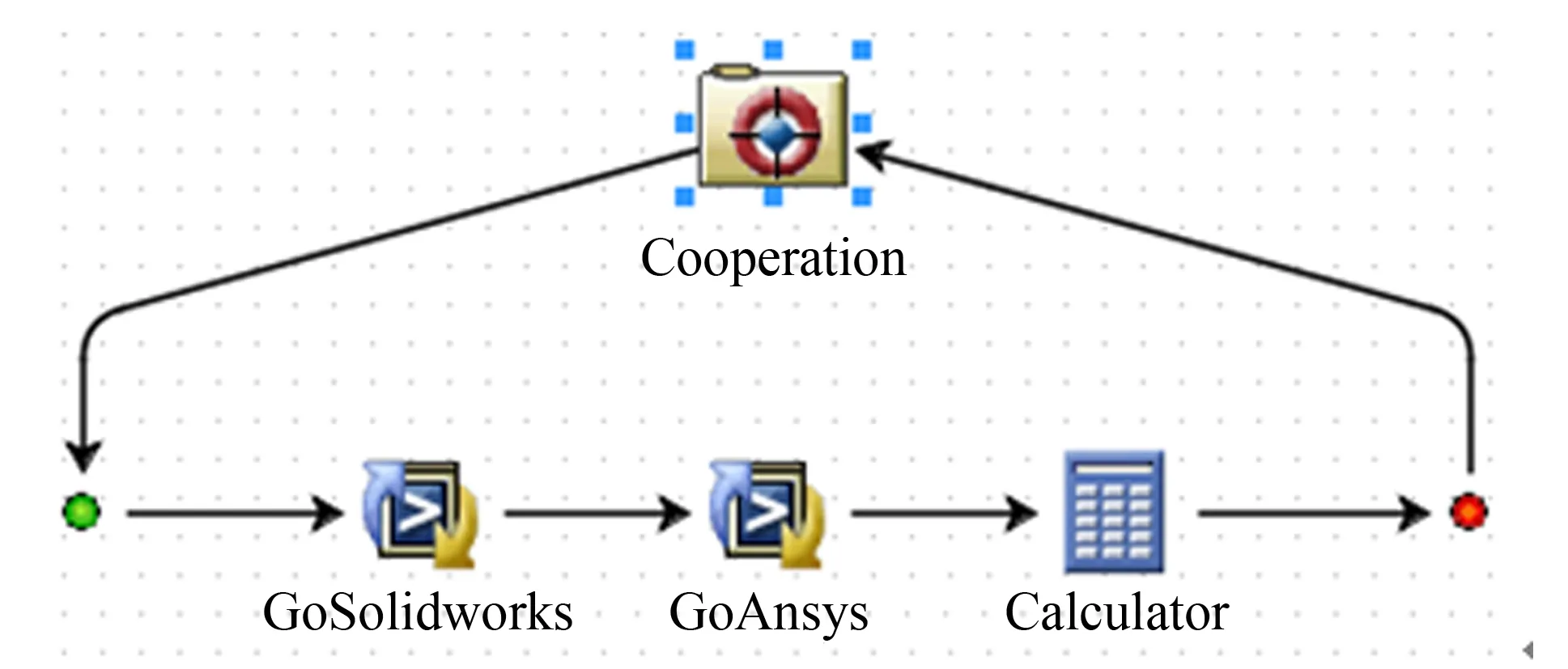
图2 合作博弈框架Fig.2 Framework of cooperative game

图3 非合作博弈框架Fig.3 Framework of non-cooperative game

3 基于Isight优化平台的多目标集成优化设计方法

Isight插入了种类齐全的优化算法，研究者可遵照具体问题须要从中选取适当的算法进行运算，这就为博弈多目标优化提供了便利. 利用Isight集成管理繁杂的数值分析流程，选择适当的优化算法自发寻找优化解空间，从而减少对象的设计成本，缩短开发周期.

利用Isight优化平台解决多目标优化设计问题的过程如下：

1) 首先对设计对象进行分析确定其设计变量、 设计目标、 约束条件，为设计问题的展开分析打下必要的基础；

2) 用Solidworks建立参数化三维模型，创建VBS(visual basic script)文件，然后对模型变量进行设置并生成IGES文件；

3) 将IGES文件导入Ansys中，建立有限元模型，然后对其进行数值计算并输出结果；

4) 基于博弈论的框架在Isight平台上集成Solidworks和Ansys，利用批处理文件GoSolidworks.bat和GoAnsys.bat的分别启动Solidworks软件和Ansys软件；

5) 选用适当的优化算法对设计对象的多目标优化设计进行解析计算.

4 悬臂梁多目标优化设计

4.1 优化问题描述与分析

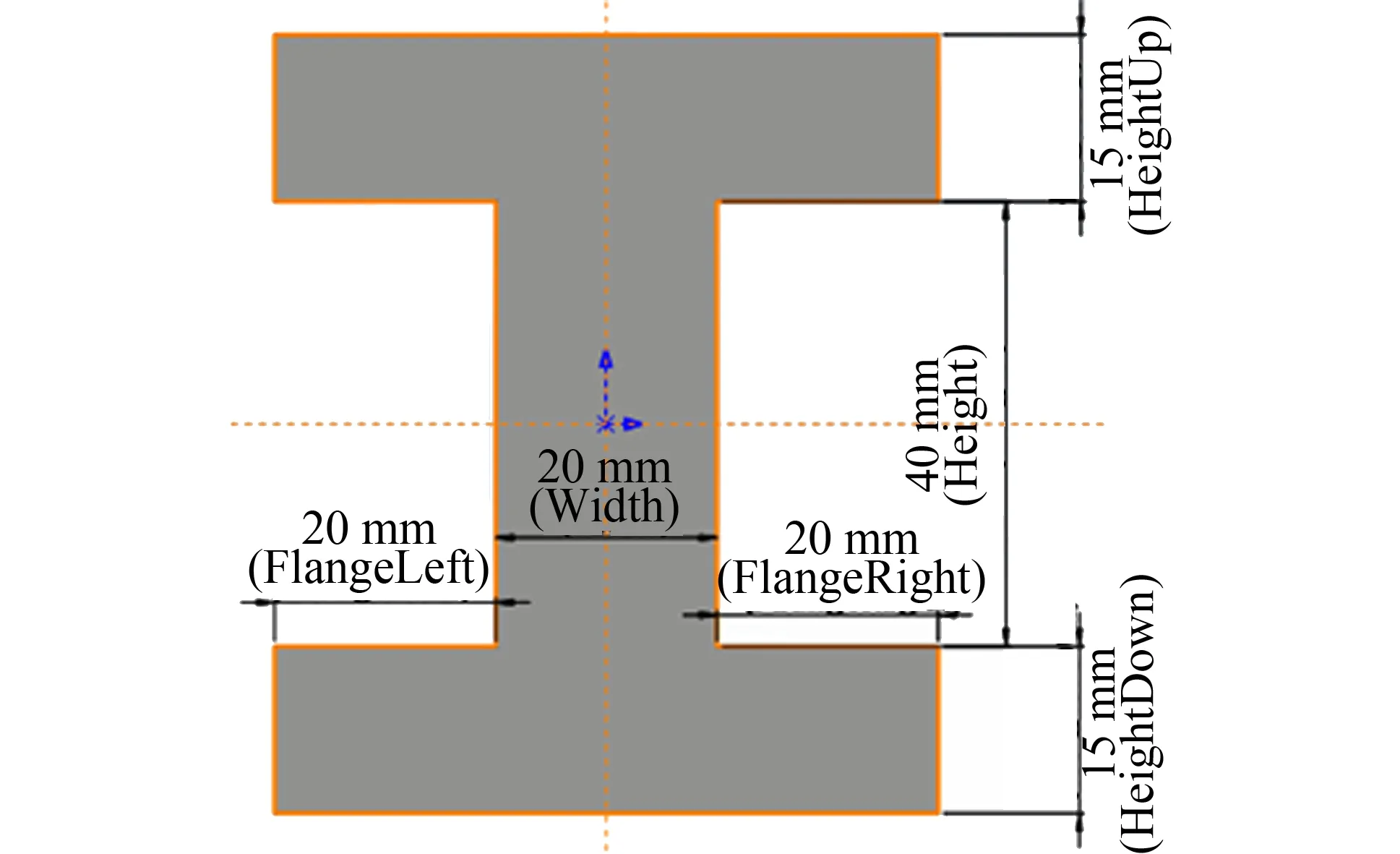
图4 悬臂梁截面及设计变量Fig.4 Cross section and design variables of cantilever beam

悬臂梁采用弹性模量为20 GPa，泊松比为0.3，密度为7.8 Mg·m-3的工字钢，工作时梁的一端固定，另一端受5 kN的弯曲载荷. 要求在强度允许的条件下尽可能减少材料，降低挠度.

根据设计要求取：

1) 设计变量. 上端高(HeightUp)，下端高(HeightDown)，右凸缘长(FlangeRight)，左凸缘长(FlangeLeft)，高(Height)，宽(Width )，长(Length)，如图4所示.

2) 设计目标. ①悬臂梁质量(Mass)尽可能小； ②挠度(DeflectionMax)尽可能小； ③最大等效应力(SeqvMax)尽可能小.

3) 约束条件. SeqvMax≤156 MPa; 0.01 m≤HeightUp≤0.03 m; 0.01 m≤HeightDown≤0.03 m; 0.01 m≤FlangeRight≤0.03 m; 0.01 m≤FlangeLeft≤0.03 m; 0.04 m≤Height≤0.05m; 0.01m≤Width≤0.03 m; 0.3 m≤Length≤0.5 m.

4.2 建立三维模型并创建VBS文件

1) 用Solidworks软件建立悬臂梁的参数化三维模型，如图5、 图6所示.

2) 创建VBS文件来启动Solidworks软件并打开相应的悬臂梁三维模型，然后将该三维模型保存为igs格式的文件为集成Ansys软件做准备. 双击执行该vbs文件后生成更新后的igs文件.

图5三维模型Fig.5 Three dimensional model

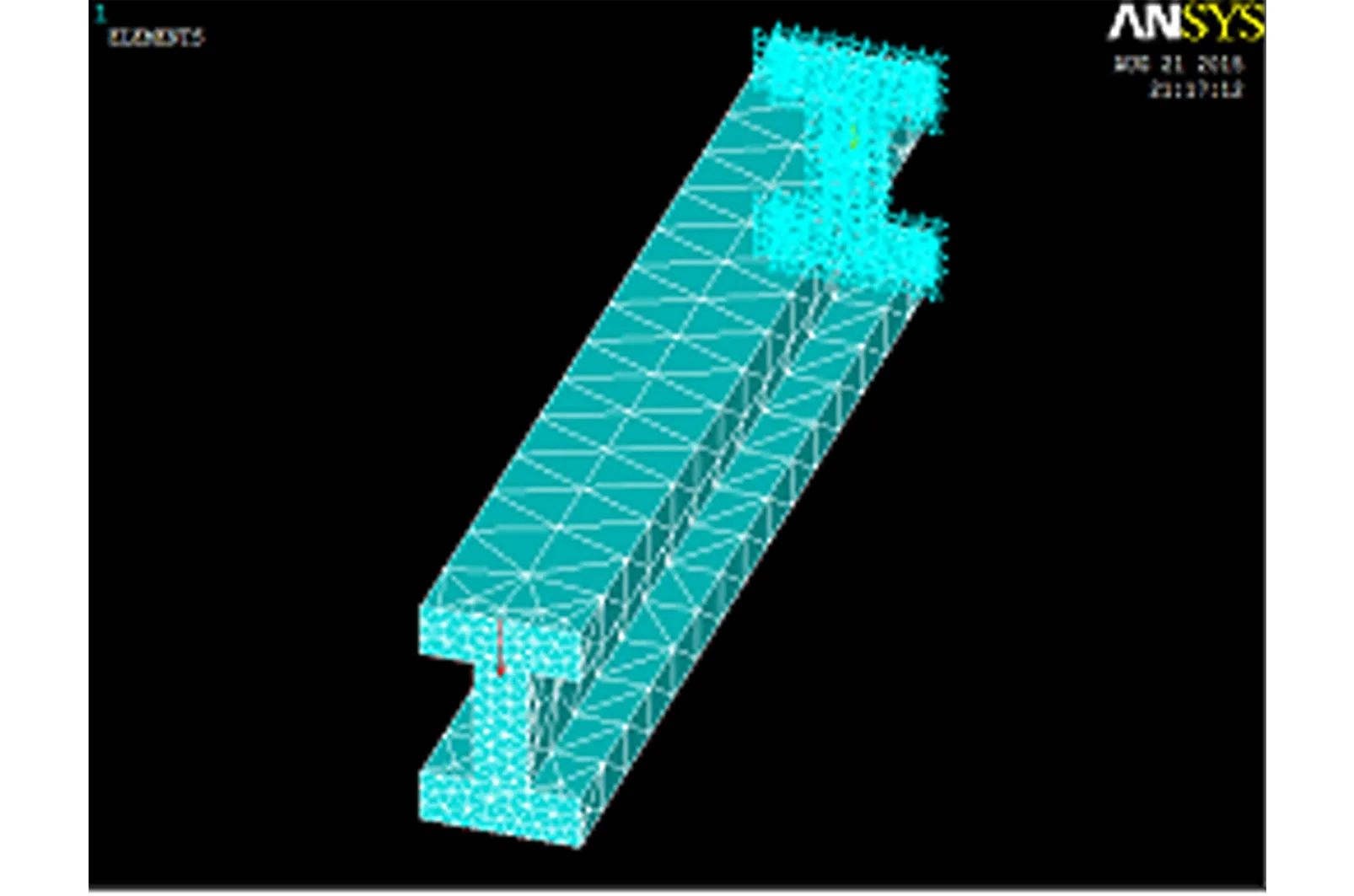
图6 有限元模型Fig.6 The finite element model

4.3 有限元分析

有限元分析主要步骤如下：

1) 将beam.igs文件导入ansys软件中；

2) 定义材料属性： 采用3维8节点固体结构单元solid185，弹性模量20 GPa，泊松比0.3，密度7.8 Mg·m-3；

3) 划分网格： 四面体自由网格；

4) 设置约束和边界条件, 如图6所示，在悬臂梁的一端添加固定约束，另一端添加5 kN的弯曲载荷；

5) 计算求解；

6) 后处理： 提取质量Mass、 挠度DeflectionMax和最大等效应力SeqvMax输出到结果文件中.

4.4 基于Isight的博弈多目标优化

基于前面悬臂梁的描述，悬臂梁优化问题有三个目标，即悬臂梁质量、 挠度和最大等效应力均尽可能小. 基于博弈论的思想，对合作博弈和非合作博弈两种方法分别进行多目标优化设计.

合作博弈多目标优化将质量、 挠度和最大等效应力三个目标进行合作博弈，选用第二代非劣排序遗传算法(NSGA-Ⅱ)进行优化，相关数据流如图7所示. 根据前面介绍的方法，进行归一化，将两目标放于同一水平. 得到合作博弈模型为：

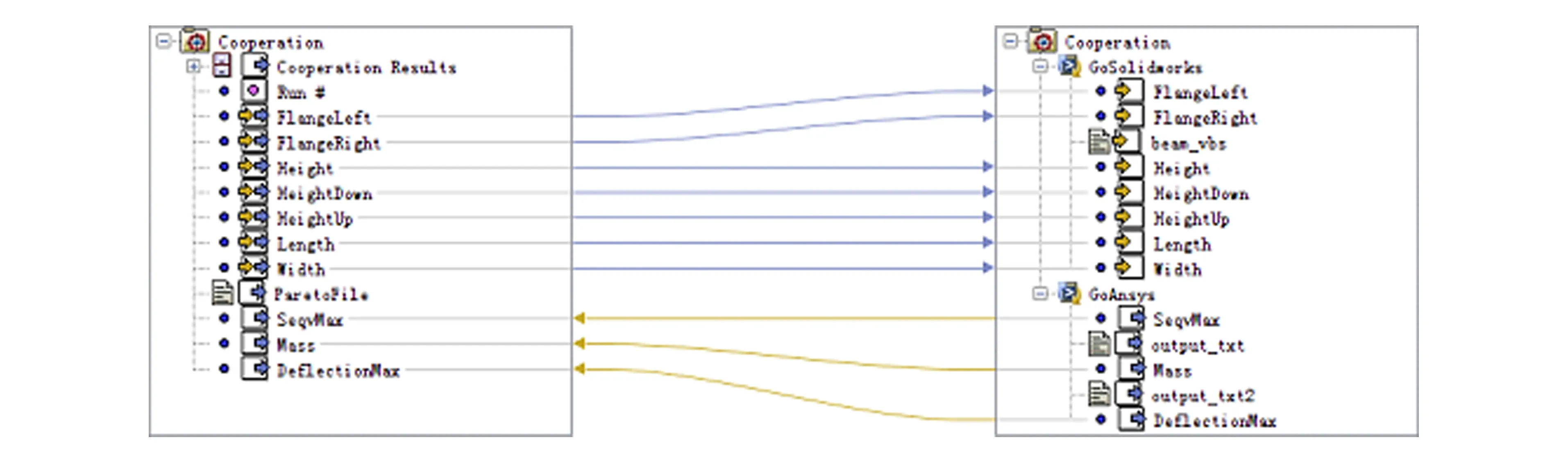
图7 合作博弈主要数据流Fig.7 Main data flow of cooperative game

其中:Z1为质量;Z2为挠度;Z3为最大等效应力.

非合作博弈多目标优化通过对数据流进行设置，利用多岛遗传算法(multi-island GA)进行优化，相关数据流如图8所示，质量目标对设计变量集FlangeRight、 FlangeLeft、 Width进行优化，挠度目标对设计变量集Height、 Length进行优化，而应力目标对设计变量集HeightUp、 HeightDown进行优化，借助于一个循环器使得各目标的最优解在各方之间互相传递，各优化器内部的数据传递合作博弈模型相同，如此迭代循环.

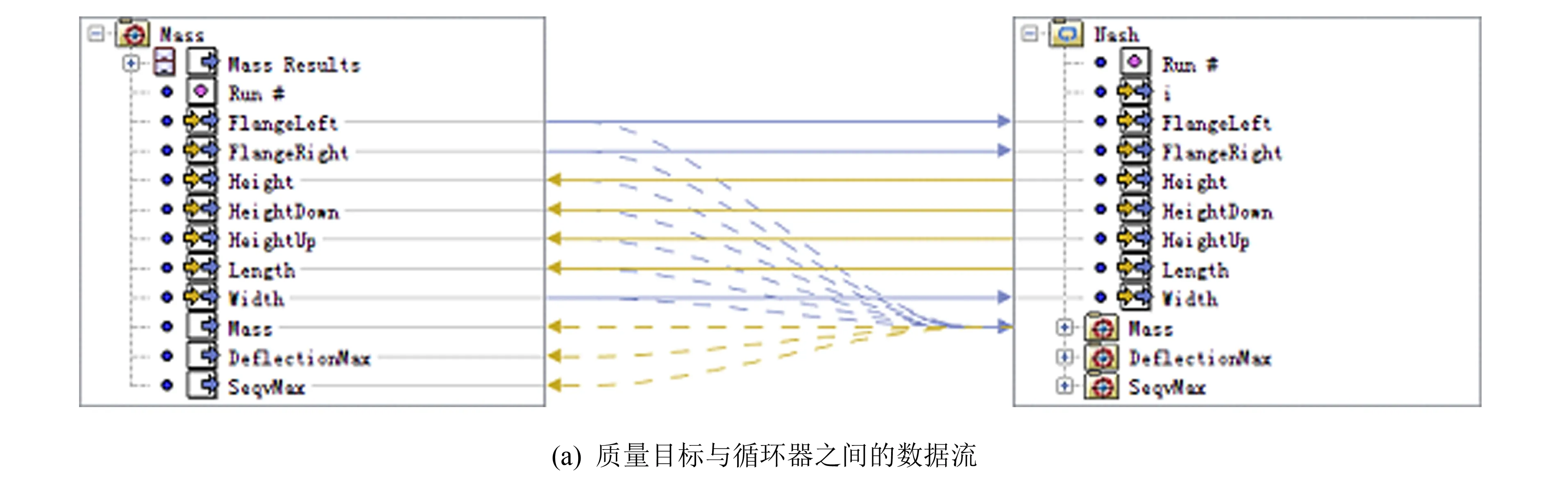
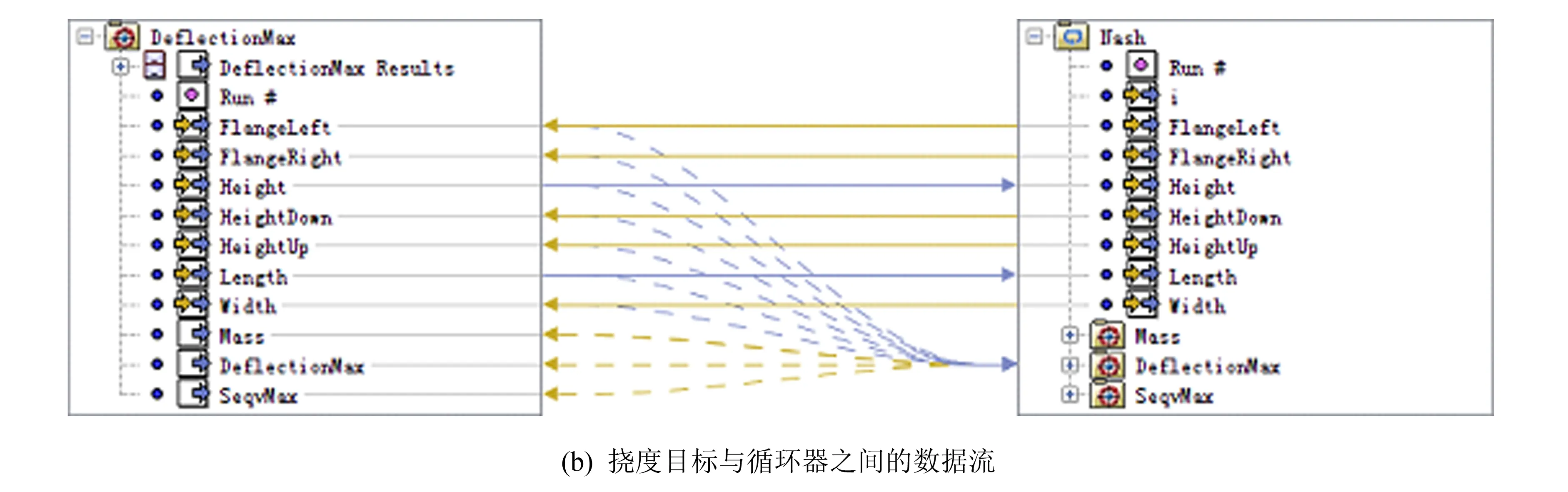
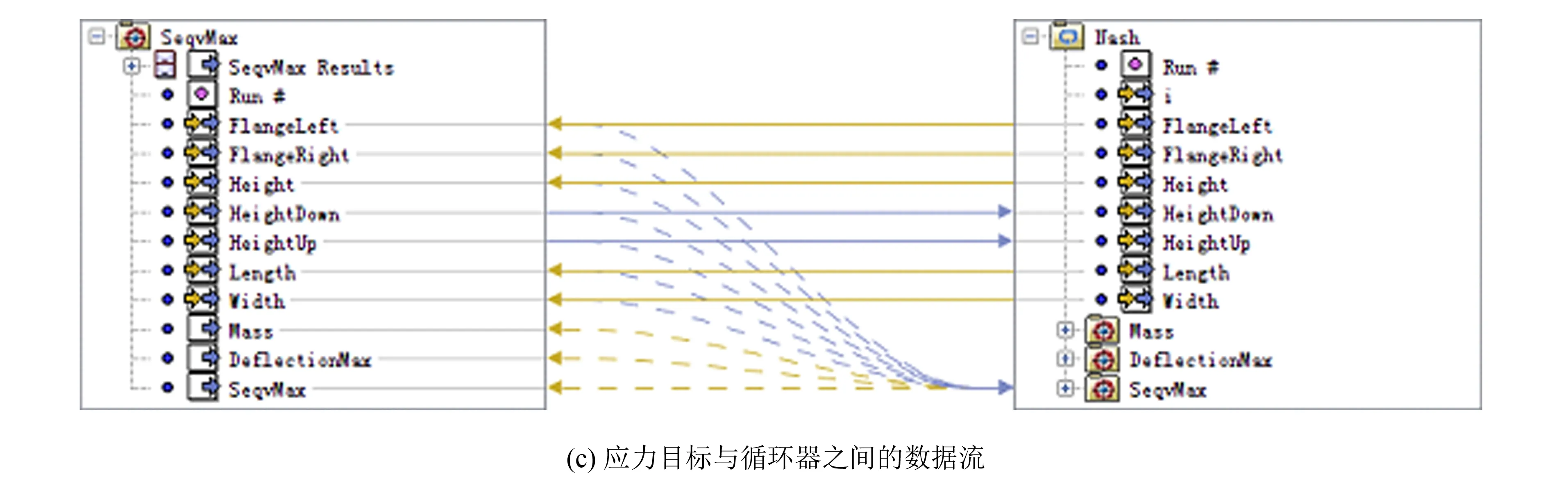
图8 非合作博弈主要数据流Fig.8 Main data flow of non-cooperative game

4.5 优化结果分析

1) 合作博弈优化结果见表1.

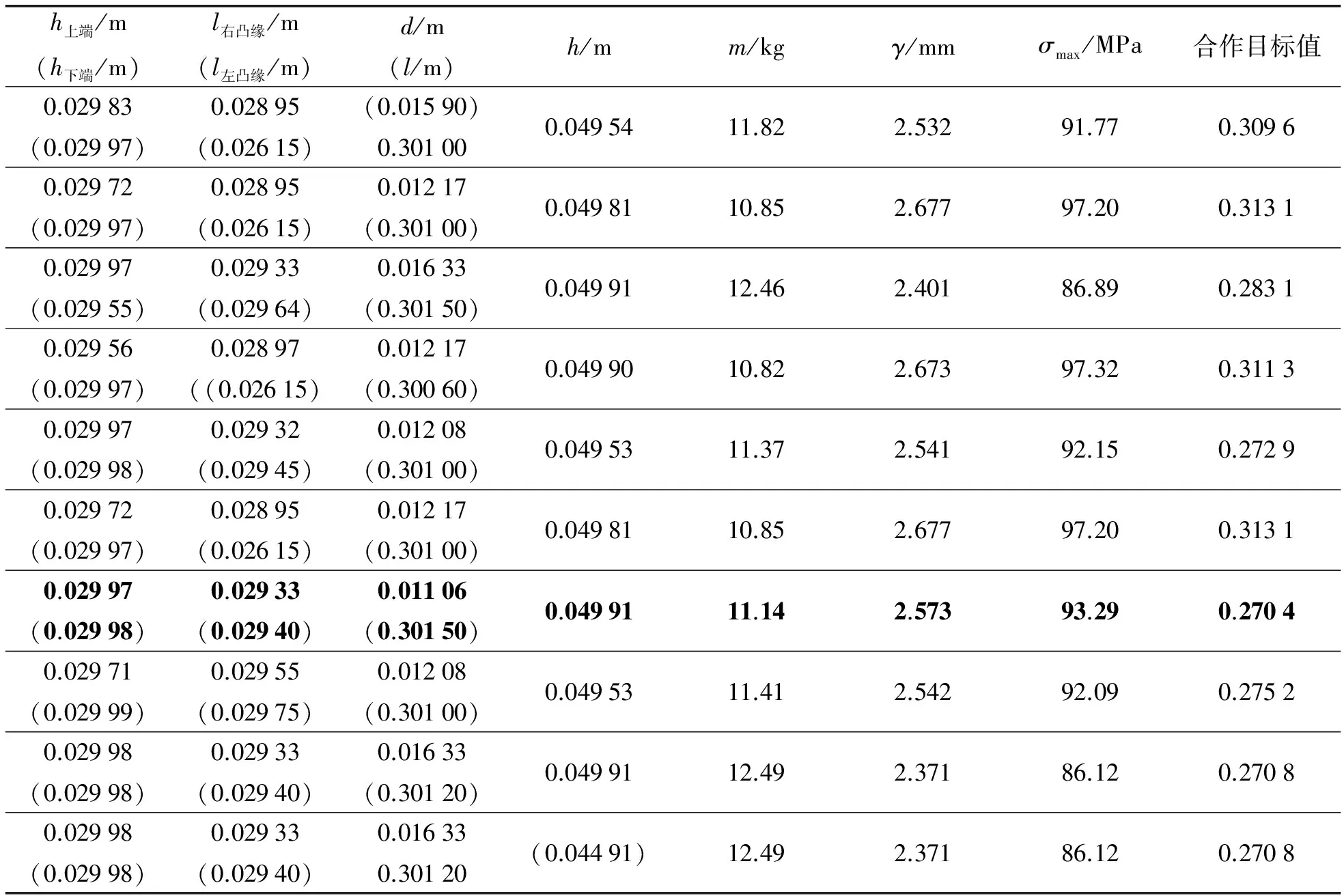
表1 合作博弈Pareto解

注： 黑体部分数据为Pareto最优解

2) 非合作博弈优化结果见表2.

表2 非合作博弈纳什均衡解

3) 优化结果分析见表3.

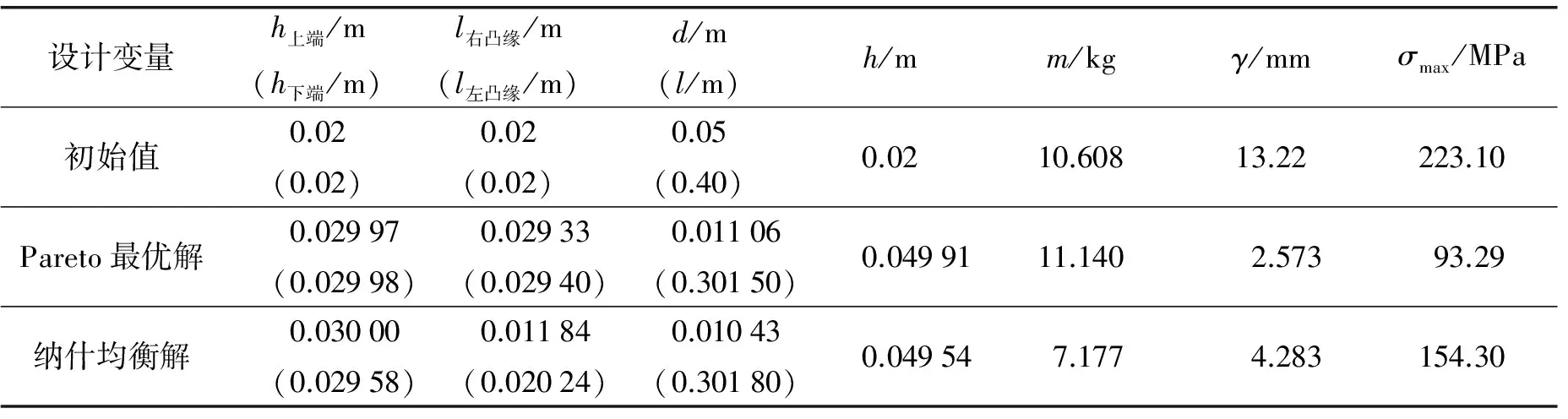
表3 优化结果比较

从表3可以看出, 不管是Pareto最优解还是纳什均衡解，其结果与优化前相比有较大改良. 虽然Pareto最优解的挠度和最大等效应力比纳什均衡解更小，但从质量来看，与纳什均衡解相比，Pareto最优解更优； 悬臂梁在满足强度要求的前提下，质量越小，所用材料就越少，成本就越低，而Pareto最优解和纳什均衡解的最大等效应力均满足设计要求.

5 结语

介绍了在Isight优化平台下运用博弈论的思想对多目标优化设计问题进行优化求解的流程. 在Isight优化平台集成Solidworks软件和Ansys软件进行建模与分析，利用博弈论思想分别建立了非合作博弈框架和合作博弈框架，设计了相应的求解算法. 以悬臂梁为例进行多目标优化设计，分别得到Pareto最优解和纳什均衡解，结果是令人满意的，表明本方法具有良好的实用性，可作为实际应用中处理多目标优化问题的一种有效可行的设计手段. 两种模型所求得的优化结果有所差异，在实际工程应用中需要根据具体问题从中选择较为合适的模型进行求解.

[1] 段明德，李言，冯浩亮，等. 高速精密数控车床床鞍结构参数多目标优化[J]. 计算机集成制造系统，2015，21(11): 2 929-2 936.

[2] KIM I Y, WECK O L D. Adaptive weighted sum method for multiobjective optimization: a new method for Pareto front generation[J]. Structural & Multidisciplinary Optimization，2006，31(2): 105-116.

[3] 韩丽霞. 求解多目标优化问题的新遗传算法[J]. 计算机科学，2013，40(6A): 64-66; 95.

[4] 杨丽丽，陈昌亚，王德禹. 基于多目标协同优化算法的卫星结构优化设计[J]. 上海交通大学学报，2014，48(10): 1 446-1 450.

[5] 王芳，饶运清，唐秋华，等. 多目标决策下Pareto非支配解的快速构造方法[J]. 系统工程理论与实践，2016，36(2): 454-463.

[6] 李洪波，徐哲，于静. 基于DSM的研发项目流程多目标仿真优化[J]. 系统工程理论与实践，2015，35(1): 142-149.

[7] NEUMAN J V，MORGENSTERN O. Theory of games and economic behavior[M]. 60th Anniversary Commemorative Ed. Princeton: Princeton University Press，2007: 32-35.

[8] 刘丹，陈亮，王伟. 一种基于合作博弈的多目标设计问题求解方法[J]. 机械设计，2014，31(8): 9-12.

[9] 王梅俊，陈亮. 运用非合作博弈的汽车盘式制动器的多目标设计决策[J]. 现代制造工程，2014(1): 9-14.

(责任编辑： 沈芸)

The application of Isight in multi-objective optimization with game

YE Wenhai，CHEN Liang，LI Liaoping

(College of Mechanical Engineering and Automation, Fuzhou University, Fuzhou, Fujian 350116, China)

Complicated multi-objective optimization design in actual engineering often meet much problem, for instance, performance goals have no explicit function relation with design variable and difficult to directly apply the traditional optimization method for design and calculation, multiple performance objectives are mutual coupling，design period is long. In order to solve these problems, the multi-objective optimization design method with game in Isight was proposed in this paper. In the Isight optimization platform, the Solidworks software and Ansys software were integrated for modeling and analysis. The game theory was employed to respectively establish the framework of cooperative game and non-cooperative game, and the genetic algorithm was adopted for optimization calculation to acquire optimal solution. The design of cantilever beam was described as an example to explain this method in this paper.

Isight platform； game theory； multi-objective design optimization； cantilever beam

10.7631/issn.1000-2243.2017.03.0391

1000-2243(2017)03-0391-07

2016-06-22

陈亮(1963-)，教授，主要从事现代设计方法、 机械设计开发等研究，chenliang@fzu.edu.cn

福建省自然科学基金资助项目(2014J01184)

TH122

A