有限维Hilbert空间中等模紧框架的一类构造方法
2017-06-09舒志彪
徐 蕤, 舒志彪
(福州大学数学与计算机科学学院, 福建 福州 350116)
有限维Hilbert空间中等模紧框架的一类构造方法
徐 蕤, 舒志彪
(福州大学数学与计算机科学学院, 福建 福州 350116)
利用Hn中已有的等模紧框架构造Hn+1中的等模紧框架; 并利用Hn中已有的紧框架来构造Hn+1中的Parseval框架. 最后给出了在这种方法下构造Rn中框架元素个数为n+1的比较稀疏的单位模紧框架的具体表达式.
等模紧框架; Parseval框架; 稀疏框架; Hilbert空间
0 引言


1 框架定义及其一些基本结论
首先简要介绍有限维Hilbert空间中框架的一些基本理论[5-6].
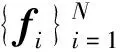
在分析和重构信号时, 合成算子、 分析算子、 框架算子起着重要的作用, 定义如下.

框架的稀疏性是近几年比较活跃的研究内容,它与目前的研究热点压缩感知具有密切的关系. 文献[14]提出框架稀疏的定义.

2 等模紧框架的构造


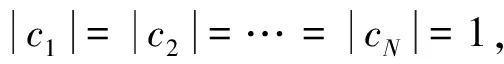
∀
对于任意g∈Hn+1,由式(1)~(4)有:

上面证明中第4个等式到第5个等式的部分推导是利用式子(3)得到, 即
当i=1, 2, …, N时, 有


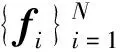
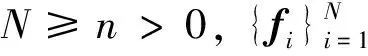

证明 由于定理3给出的框架与定理2给出的框架具有相同的性质, 那么定理2的证明中得到的式(1)~(4)这4个等式在这里也成立.
对于任意g∈Hn+1,由式(1)~(4)有:
对于任意的i=1, 2, …, N, 得到
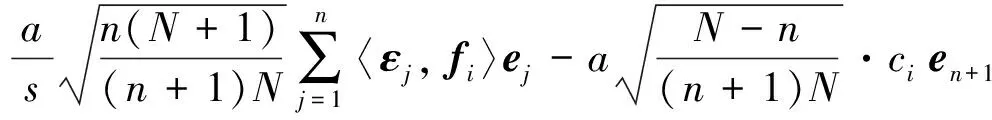
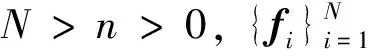

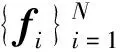
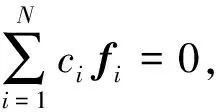
对于任意g∈Hn+1,由式(5)~(6)式有:

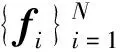
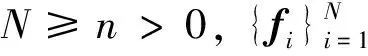

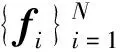
对于任意g∈Hn+1,由式(7)~(8)式有:
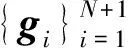

[1] TSILIGIANNI E V, KONDI L P, KATSAGGELOS A K. Construction of incoherent unit norm tight frames with application to compressed sensing[J]. IEEE Transactions on Information Theory, 2014, 60(4): 2 319-2 330.
[2] GOYAL V K. Single and multiple description transform coding with bases and frames[M]. Philadelphia: SIAM, 2002.
[3] GOYAL V K, KOVACEVIC J. Optimal multiple description transform coding of gaussian vectors[C]//Proceedings of Data Compression Conference. [S.l.]: IEEE, 1998: 388-397.
[4] GOYAL V K, KOVACEVIC J, VETTERLI M. Quantized frame expansions as source-channel codes for erasure channels[C]//Proceedings of Data Compression Conference. [S.l.]: IEEE, 1999: 388-397.
[5] CASAZZA P G, KUTYNIOK G. Finite frames: theory and applications[M]. Boston: Birkhǎuser, 2012.
[6] CHRISTENSEN O. An introduction to frames and Riesz bases[M]. Boston: Birkhǎuser, 2003.
[7] CASAZZA P G, KOVACEVIC J. Equal-norm tight frames with erasures[J]. Advances in Computational Mathematics, 2003, 18(2): 387-430.
[8] FENG D, WANG L, WANG Y. Generation of finite tight frames by householder transformations[J]. Advances in Computational Mathematics, 2006, 24(1): 294-309.
[9] CASAZZA P G, LEONHARD N. Classes of finite equal norm parseval frames[J]. American Mathematical Society, 2008, 451:11-32.
[10] CASAZZA P G, FICKUS M, HEINECKE A,etal. Spectral tetris fusion frame constructions[J]. Journal of Fourier Analysis and Applications, 2012, 18(4): 828-851.
[11] CASAZZA P G, FICKUS M, MIXON D G,etal. Constructing tight fusion frames[J]. Applied and Computational Harmonic Analysis, 2011, 30(2): 175-187.
[12] CASAZZA P G, HEINECKE A, KORNELSON K. Necessary and sufficient conditions to perform spectral tetris[J]. Linear Algebra and Its Applications, 2013, 438(5): 2 239-2 255.
[13] ABDOLLAHI A, MONFAREDPOUR M. Tetris tight frames construction via hadamard matrices[J/OL]. Abstract and Applied Analysis, (2014-03-17) [2014-12-09]. http://dx.doi.org/10.1155/2014/917491.
[14] CASAZZA P G, HEINECKE A, KRAHMER F. Optimally sparse frames[J]. IEEE Transactions on Information Theory, 2011, 57(11): 7 279-7 287.
(责任编辑: 林晓)
A class of methods for constructing equal-norm tight frames in a finite dimensional Hilbert space
XU Rui,SHU Zhibiao
(College of Mathematics and Computer Science, Fuzhou University, Fuzhou, Fujian 350116, China)
We use the existing equal-norm tight frames forHnto construct equal-norm tight frames forHn+1. We also use the existing tight frames forHnto construct Parseval frames forHn+1. In addition, we give a detailed expression of sparse unit-norm tight frames withn+1 vectors forRnin this construction.
equal-norm tight frame; Parseval frame; sparse frame; Hilbert spaces
10.7631/issn.1000-2243.2017.03.0323
1000-2243(2017)03-0323-06
2015-06-02
舒志彪(1958-),副教授,主要从事小波分析、 图像处理等方面研究, fzb@fzu.edu.cn
福建省自然科学基金资助项目(2014J01007 ); 福建省教育厅A类资助项目(JA14041); 福州大学科技发展基金资助项目(2012-XQ-29)
O177.1
A
