基于二维谱向量的中段弹道目标平动补偿*

王义哲， 冯存前,2， 赵 双， 陈 彬

(1.空军工程大学 防空反导学院，陕西 西安 710051； 2.信息感知技术协同创新中心，陕西 西安 710077)

基于二维谱向量的中段弹道目标平动补偿*

王义哲1， 冯存前1,2， 赵 双1， 陈 彬1

(1.空军工程大学 防空反导学院，陕西 西安 710051； 2.信息感知技术协同创新中心，陕西 西安 710077)

弹道目标中段的运动是微动与平动的复合，为了提取目标的微多普勒信息，必须先进行平动补偿。首先分析并建立了弹道目标中段的运动模型，说明了将平动近似描述为二阶多项式的合理性，在此基础上，提出了一种基于二维谱向量的平动参数估计方法。利用频域特征与平动参数对应的关系，对细化后回波信号频谱的能量分布和重心位置进行了量化，从而分别实现了加速度和速度的高精度补偿。仿真实验结果表明：在多目标和强噪声的环境下，该方法具有良好的估计性能。

目标识别； 弹道目标； 微动； 平动补偿； 频谱细化

0 引 言

随着弹道导弹突防能力的快速发展，弹道目标识别技术的重要性也愈发突出。目前，基于涂覆层特征、结构特征及常规运动特性的传统特征识别技术已经难以从复杂目标群中识别出真弹头。微动,作为运动目标的固有属性之一，可以表征目标的精细运动特性，近年来已成为感兴趣目标识别的重要依据[1]。弹道目标的微动叠加在高速平动的基础上，而平动分量的存在会导致回波多普勒谱产生折叠和变形[2,3]，因此，在提取弹道目标微动信息之前，必须先进行平动补偿。

现有的平动补偿方法可以分为两类。第一类主要基于时频分析，如文献[4]先提取最强散射点的瞬时多普勒,再根据多普勒率得出对应的平动多普勒;文献[5]先利用曲线的光滑性实现微多普勒曲线的分离，再进行经验模态分解从而求出平动趋势项。此类方法对信噪比(SNR)要求较高，当时频分布受噪声污染较严重时，性能急剧下降,此外，由于平动带宽通常大于脉冲重复频率，微多普勒将被截成多段，也会限制此类方法的适用范围。第二类方法属于频域处理方法，以高红卫提出的频谱重排法为代表[2,3]，该方法计算量小、易于实现，但文献[2，3]建立的运动模型较为简单，且仅考虑了频谱的局部特征，估计平动参数时容易陷入局部最优值。

针对上述问题，本文提出了一种利用精细频谱特征的平动补偿方法。在构建弹道目标中段复合运动模型的基础上，先通过频谱细化处理得到回波信号的高分辨频谱特征，再以谱熵和重心频率构成的二维谱向量为指标，对频谱进行条件最优搜索，实现了平动参数的高精度估计。

1 弹道目标中段运动模型

1.1 平动模型

当雷达目标在大气层外飞行时，大气十分稀薄，可忽略其阻力的影响，视弹道目标的飞行轨道模型为“二体轨道模型”，则平动可以描述为位于速度矢量与地球引力矢量所决定的平面内的运动[6]。

在平动模型构建中，二阶及更高阶加速度可忽略不计，也就是将短时间内的中段平动近似为二阶多项式

rtr(t)=r1+vtrt+atrt2/2

(1)

式中r1为初始径向距离，vtr,atr分别为弹道目标在t时刻的速度和加速度。

1.2 微动模型

以无翼锥体弹头为例建立微动模型，由于理想散射点模型与弹头的实际情况存在较大差异，本文采用文献[7]中提出的滑动型散射中心。如图1所示，O-WUV为雷达观测坐标系，Oi-XiYiZi为弹头i的滑动坐标系。θi,ωci分别为弹头i的进动角及进动角频率，(αi,βi)为观测雷达到弹头i的视线(LOSi)在Oi-XiYiZi中的视角，Hi,di,Oi分别为弹头i的高、底面直径及质心，hi为弹头i的质心Oi到底面的距离。Zi轴为弹头i对应的进动轴的方向，Yi轴为Zi轴顺时针旋转90°的指向，Xi轴符合右手螺旋准则，αi为LOSi在OiXiYi平面的投影与Xi轴的夹角，βi为LOSi与弹头i自身的旋转轴之间的夹角。

图1 弹道目标微动模型

考虑散射点的遮蔽问题，设雷达的入射电磁波与目标i底面交于一点Bi，另一点已被遮蔽，则目标i的顶点Ai、底面交点Bi在t时刻处的微距离分别为[7]

(2)

式中 [lni,n∈N+]为与θi,βi有关的系数，具体关系式见文献[7]。

假设雷达发射工作频率为fc的单频信号，经目标散射和基带变换后得到回波s(t)，对s(t)相位项进行求导，得到i个目标的多普勒为

(3)

式中i=N+;∪(·)为包含关系;φ(t)为s(t)的相位项;c为光速。括号中前一项产生平动多普勒，后两项产生微多普勒。

2 基于二维谱向量的平动参数估计

2.1 平动参数分析

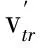
(4)

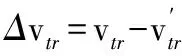
由式 (1)～式(4)可以看出，目标回波在时频域即多普勒谱域中，微多普勒本身具有一定的带宽，而平动项的调制带宽一般远大于微多普勒带宽，导致微多普勒谱淹没在平动多普勒谱中，使得微多普勒参数的提取变得十分困难，平动补偿的关键就在于精确估计出Δvtr和atr这两个参数。

信息熵可以度量信源消息平均携带信息量大小，文献[8]将信息熵引入到信号处理领域，并提出了谱熵的概念。设有信号时间序列{x(n)|n=1,2,…,N}，其对应的频谱序列为{X(k)|k=1,2,…,N}，令

(5)

式中i=1,2,…,N，即qi为第i条幅值谱在整个谱中所占的百分比,则信号谱熵被定义为

(6)

谱熵刻画了信号的谱型结构情况，易知，单频信号的谱熵最小且为0，白噪声信号的谱熵最大，为logN。为了使长度不同的信号的谱熵具有统一性，并将谱熵规整到0与1之间，可定义相对谱熵为

Er(X)=H(X)/logN

(7)

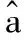
速度Δvtr不会影响频谱的能量分布，只是将频谱进行整体平移，无法用谱熵进行衡量。而频谱的平移表现为重心位置的变化，因此考虑引入频谱的第二维向量，即重心位置维指标。定义频谱的重心频率为

(8)

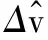
2.2 频谱细化处理

针对包含多个密集频率成分的离散频谱，线性调频Z变换(Chirp Z transform,CZT)具有良好的频谱细化特性，其基本思想是在单位圆上以等角度间隔进行频率点采样。设X(z)表示序列x(n)的Z变换，则CZT法可计算下列给定点Zk上的X(Zk)

Zk=AW-k,k=0,1,…,M-1

(9)

式中A=A0e-jθ0，W=W0e-jφ0，A0和θ0分别为起始抽样点Z0的矢量半径长度和相角，W0为螺旋线的伸展率，φ0为两相邻抽样点之间的角度差，M为所要分析复频谱的抽样点数，根据所需的频率分辨率来设定。该算法可以在不增加数据长度的前提下，通过插值增加快速傅里叶变换(FFT)变换点数，较快捷地实现频率的细化。

综上所述，平动补偿算法的基本流程如下：

1)利用CZT法处理雷达录取的目标回波s(t)，得到细化的频谱S(k)，并根据弹道特性，分别设定atr和Δvtr的分布范围(amin,amax),(vmin,vmax)。

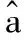
(10)

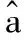
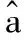
(11)

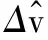
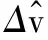
(12)

3 仿真分析

设雷达发射工作频率fc=10 GHz的单频信号，脉冲重复频率fPRF=1 000 Hz，观测时间为4 s，SNR=-5 dB。空间中存在2个锥体目标1和目标2。目标1的参数设置为H1=2.5 m,h1=0.9 m,d1=1.6 m,(α1,β1)=(50.6°,40.9°),θ1=10°,ωc1=2πrad/s;目标2的参数为H2=2.8 m,h2=1.2 m,r2=2.0 m,(α2,β2)=(52.4°,38.8°),θ2=12°,ωc2=3πrad/s。由于可认为单个波束内的目标具有相同的平动趋势，两目标的平动参数都设为Δvtr=3.52 m/s，atr=-6.37 m/s。

利用上述模型产生目标回波并进行奇异值分解(SVD)去噪，粗补偿后回波信号的短时傅立叶变换(STFT)结果如图2(a)所示。由于平动速度和加速度的存在，目标的微多普勒谱在时频图上出现了折叠和变形，与理论分析一致。同时，时频图已被噪声严重污染，文献[4]中的Viterbi算法及文献[5]中的骨架提取方法都将失效。利用线性调频CZT算法处理回波，得到细化的频谱如图2(b)所示，此时的频谱占满了整个频带，可以发现在某些频率位置处的噪声幅值已经与信号幅值相当，而文献[2]提出的中心法及文献[3]提出的峰值法、模板法都需先搜索频谱最大值位置从而进行频谱校正，这就很容易发生定位错误。

图2 粗补偿后的回波信号

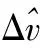
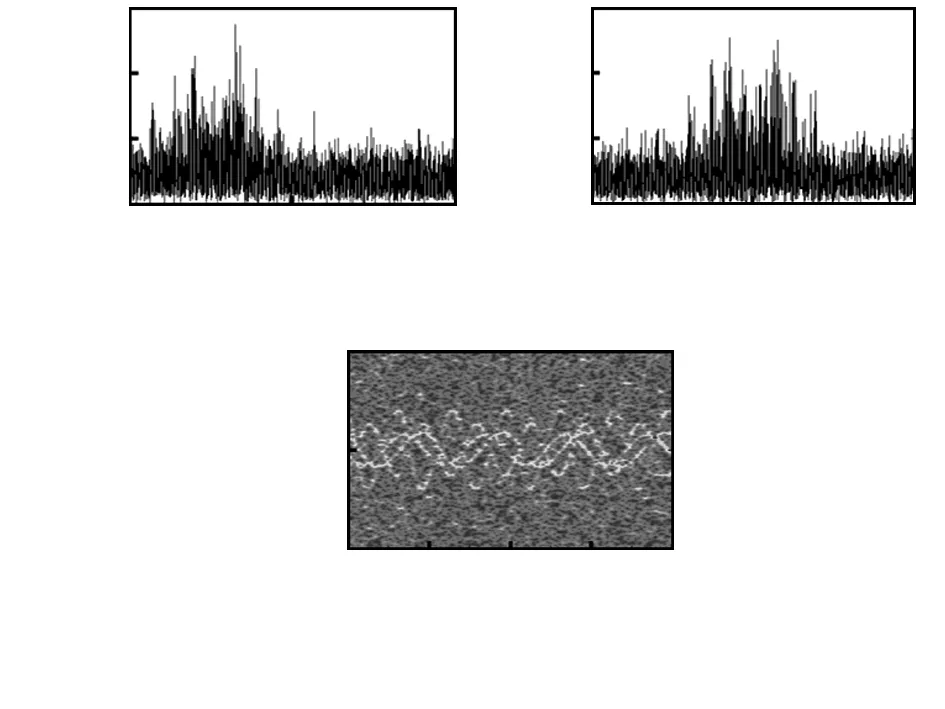
图3 平动补偿过程

进一步分析不同方法的补偿效果，其它参数设置不变，在不同信噪比条件下进行100次蒙特-卡罗仿真，本文方法求速度和加速度时都采用3次估计，得到的均方根误差(rootmeansquareerror,RMSE)如表1所示。从表1可以看出，本文方法明显优于文献[2]和文献[3]方法，当SNR≥-6dB时，本文算法可实现对速度和加速度的高精度估计；当SNR<-6dB时，RMSE突然增大，这是由于此时频谱中较多频率位置处的噪声幅值开始淹没并超过信号幅值，使得二维谱向量特征无法继续有效反映回波信号中平动分量对频谱分布的影响。

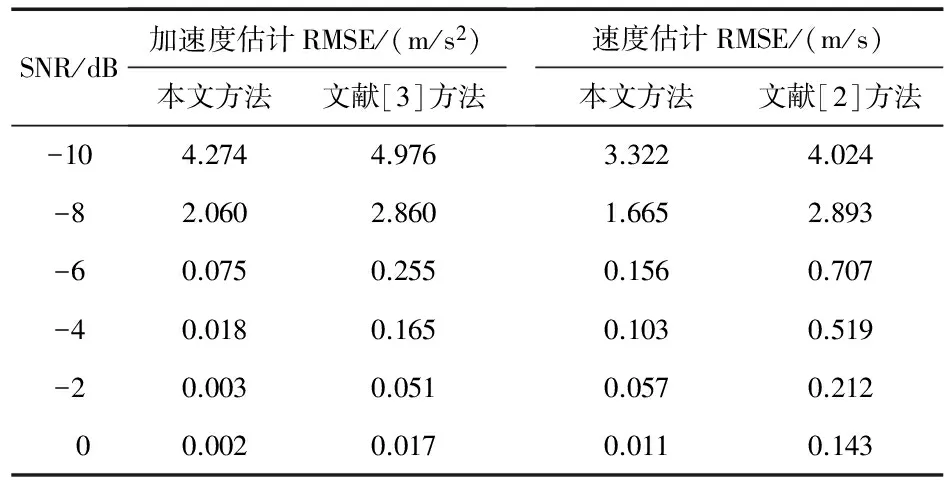
表1 平动参数估计性能

4 结束语

针对弹道目标平动补偿问题，本文提出了一种基于二维谱向量的平动参数估计方法。本文方法无需利用时频域特征，具有较强的抗噪性，当SNR≥-6 dB时，对加速度和速度都能实现有效补偿。此外，本文方法仅需在频域进行处理，因此相对于时频分析法还具有简单有效、计算量小的优点，适于实际工程应用。

[1] Chen V C.Advances in applications of radar micro-Doppler signatures[C]∥Proceedings of IEE Antenna Measurements & Application,France:2014:1-4.

[2] 高红卫,谢良贵,文树梁,等.速度对微多普勒的影响及其补偿研究[J].航天电子对抗,2008,24(4):46-50.

[3] 高红卫,谢良贵,文树梁,等.加速度对微多普勒的影响及其补偿研究[J].宇航学报,2009,30(2):705-711.

[4] 杨有春,童宁宁,冯存前,等.利用最强散射点信息的平动补偿与微多普勒提取[J].西安电子科技大学学报,2012,39(6):147-153.

[5] 罗迎,柏又青,张 群,等.弹道目标平动补偿与微多普勒特征提取方法[J].电子与信息学报,2012,34(3):602-608.

[6] 李志汇，刘昌云，于 洁.基于信息增量的弹道目标协同跟踪方法[J].传感器与微系统,2015,34(6):33-36.

[7] Ma L,Liu J,Wang T,et al.The micro-Doppler character of sli-ding-type scattering center on rotationally symmetric target[J].Scientia Sinica Informationis,2011,54(9):1957-1967.

[8] 申 弢,黄树红,韩守木,等.旋转机械振动信号的信息熵特征[J].机械工程学报,2001,37(6):94-98.

Translational motion compensation of ballistic targets in midcourse based on 2D spectral vector*

WANG Yi-zhe1， FENG Cun-qian1,2， ZHAO Shuang1， CHEN Bin1

(1.Air and Missile Defense College,Air Force Engineering University，Xi’an 710051,China；2.Collaborative Innovation Center of Information Sensing and Understanding，Xi’an 710077,China)

As the motion of ballistic targets in midcourse is the complex motion of micro-motion and translation,the translational motion should be compensated to extract micro-Doppler information.The motion model for ballistic targets in midcourse is analyzed and constructed first, and then the rationality of regarding translational motion as a second order polynomial is illustrated.On this basis,a novel method based on two-dimensional spectral vector is proposed to estimate translation parameters.Exploiting the relationship between frequency spectrum and translation parameters, the energy distribution and center of gravity in frequency domain are quantized for zoomed echo signal.Thus the speed and acceleration can be compensated with a high precision.Simulation results show this method exhibits excellent estimation performance under group-target and strong noise environment.

target recognition; ballistic targets; micro-motion; translation motion compensation; spectrum zoom

2016—06—02

国家自然科学基金资助项目(61372166)

10.13873/J.1000—9787(2017)06—0066—04

TN 957

A

1000—9787(2017)06—0066—04

王义哲(1992-)，男，硕士，主要研究方向为雷达信号处理,E—mail：wangyizhe813@163.com。

冯存前(1975-)，男，教授，从事雷达信号处理与电子对抗领域研究工作。