复平面闭曲线的绕数及其应用

林庆泽， 尚亚东

（1.广东工业大学 应用数学学院，广东 广州 510520；2.广州大学 数学与信息科学学院,广东 广州 510006）

复平面闭曲线的绕数及其应用

林庆泽1，2， 尚亚东2

（1.广东工业大学 应用数学学院，广东 广州 510520；2.广州大学 数学与信息科学学院,广东 广州 510006）

给出实参数闭区间上的复平面连续闭曲线的绕数的一种定义并证明它的一些重要的性质，由此得到关于复数多项式的代数基本定理的一种推广形式。利用复平面上连续闭曲线的绕数性质给出Brouwer不动点定理的2维形式的一个证明。

闭曲线；绕数；代数基本定理；不动点定理

0 引言

在复变函数论中，Cauchy积分定理的推导需要利用闭曲线的绕数性质，而且Cauchy积分定理的表达公式中也包含着闭曲线的绕数：

定理1(Cauchy积分定理)[1-2]如果函数f(z)是开盘上的解析函数且是△上的连续可微的闭曲线，那么对于不在上的任一点z0，都有

这里我们给出(1)式所定义的等式的合理性的解释：若将闭曲线用复数指数形式来表示（其中，则因此

本文从研究点z0=(0,0)时的情形出发，证明了连续闭曲线绕数的一些重要的性质，并由此得到代数基本定理的一种以极限的形式来表示的推广形式，最后利用连续闭曲线的绕数性质给出Brouwer不动点定理的2维情形的一个简短的证明，由此显示出闭曲线的绕数性质在处理分析问题中的重要性。

1 绕数的若干性质

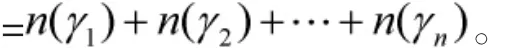
我们证明这样定义的绕数是合理的。

证明 这是显然的。证毕。

证明 存在着α＞0，使得∀q∈（-∞，0]，∀t∈[a，b]，有取三角多项式P(t)使得∀t∈[a，b]，，故从命题2知，n(P)=0，亦即n()=0。证毕。

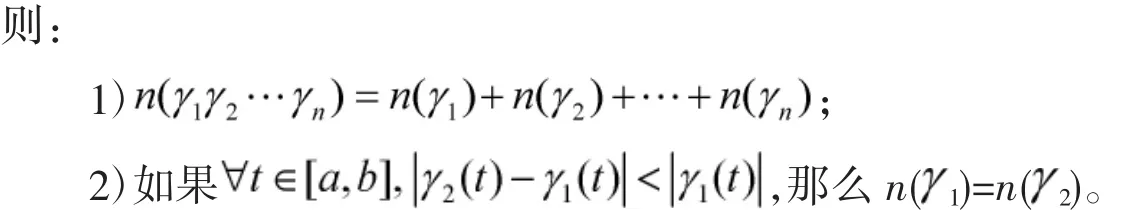
证明 1）由命题4，这是显然的。

2 绕数的若干应用

2.1 代数基本定理的推广

命题8 令f(z)是定义在复平面上的连续复值函数，如果存在一个正整数n和一个非零复数z0，使得，那么方程f(z)=0在复数域上至少有一个根。

由命题8，我们直接得到下面的代数基本定理：

定理2（代数基本定理）[2，7]如果且则多项式方程在复数域上至少有一个根。

2.2 Brouwer不动点定理的证明

2）取定任一r0∈[0，1]，因为的连续性，存在着δ＞0，使得当时，因此由命题7知，从而是关于r∈[0，1]的连续函数。

定理3（Brouwer不动点定理）[8]记是到的连续函数，则存在一点，使得

[1]AHLFORS L V.Complex analysis[M].3th ed.Beijing：China Machine Press，2004：114-120.

[2]华罗庚.高等数学引论：第三分册[M].北京：高等教育出版社，2009：95-97.

[3]MCINTYRE M，CAIRNS G.A new formula for winding number[J].Geometriae Dedicata，1993，46（2）：149-159.

[4]华罗庚.高等数学引论：第二分册[M].北京：高等教育出版社，2009：96-99.

[5]华东师范大学数学系.数学分析：下册[M].第4版.北京：高等教育出版社，2010：185-201.

[6]ZORICH V A.Mathematical analysis（I）[M].Berlin：Springer-Verlag，2004：526-551.

[7]RUDIN W.Principles of mathematical analysis[M].New York：McGraw-Hill，2004：184-190.

[8]BORDER K C.Fixed point theorems with applications to eeconomics and game theory[M].Cambridge：Cambridge University Press，2009：28-30.

The Winding Number of Closed Curve in the Complex Plane and its Applications

LIN Qinɡze1，2，SHANG Yɑdonɡ2

（1.School of Applied Mathematics，Guangdong University of Technology，Guangzhou Guangdong 510520，China；2.School of Mathematics and Information Science，Guangzhou University，Guangzhou Guangdong 510006，China）

A definition of winding number of the continuous closed curve in the complex plane，with real parameter interval，is defined，and its several important properties are proven.Base on these，a generalization of the fundamental theorem of algebra concerned with the complex polynomials is deduced.Finally，by virtue of the properties of the winding number of the continuous closed curve in the complex plane，the two-dimensional form of the Brower's fixed point theorem is proven.

Closed Curve；Winding Number；Fundamental Theorem of Algebra；Fixed Point Theorem

O174.5

A

1009-8666（2017）04-0001-05

10.16069/j.cnki.51-1610/g4.2017.04.001

［责任编辑、校对：李书华］

2016-11-06

林庆泽（1994—），男，广东揭阳人。广东工业大学硕士研究生，研究方向：数学与数据统计分析；尚亚东（1963—），男，陕西周至人。广州大学教授，博士生导师，研究方向：非线性偏微分方程理论与应用。