基于模态参数识别的悬架系统状态监测方法及试验研究

李苗硕，谷丰收，王铁，李国兴，，王永红，鹿星晨

（1.太原理工大学机械工程学院车辆工程系，山西 太原 030024；2.哈德斯菲尔德大学工程与效能中心，曼彻斯特 HD1 3DH；3.大运汽车股份有限公司，山西 运城 044000）

基于模态参数识别的悬架系统状态监测方法及试验研究

李苗硕1，谷丰收2，王铁1，李国兴1，2，王永红3，鹿星晨1

（1.太原理工大学机械工程学院车辆工程系，山西 太原 030024；2.哈德斯菲尔德大学工程与效能中心，曼彻斯特 HD1 3DH；3.大运汽车股份有限公司，山西 运城 044000）

悬架系统直接关系到车辆的安全性、平顺性和操稳性，由于路面激励是随机激励，对悬架系统的状态监测一直是研究难点。该文提出一种新的悬架状态监测方法，利用仅需输出的平均相关随机子空间法识别模态参数，再通过模态参数变化对故障造成的悬架刚度变化进行监测。首先对平均相关随机子空间法在较高阻尼比下的识别效果进行分析，验证算法在悬架监测中的可行性；然后基于车辆七自由度振动模型对模态参数进行仿真识别，分析路面激励及噪声对识别结果的影响，并提出基于振型和模态能量的监测方法；最后设计利用9轴MEMS惯性传感器的试验方案对正常及故障状态进行监测，验证方法的可信度。

模态参数识别；悬架系统；平均相关随机子空间法；状态监测；MEMS

0 引言

有关车辆悬架系统的大量研究结果表明，车辆悬架系统直接关系到车辆通过性、运行稳定性、平顺性、安全性以及操纵稳定性[1-4]。为了确保悬架装置正常运行，对悬架系统进行状态监测成为近期研究的热点[5-6]。有些研究采用数据驱动方法，即基于对某振动信号的直接测量进行时域和频域分析来实现故障检测[7-9]。但悬架系统的振动与行车速度和路面激励的耦合关系较为复杂，为特征不明显的非平稳随机信号，较难有效提取故障信息。近年来，很多研究将基于模型的监测方法作为重点，并取得了一定的成功[10-11]。

随机子空间法（SSI）作为随机激励下仅需输出的识别方法，识别准确且所需设备简便，得到了很多研究者的重视。Yuan[12]用随机子空间法估计车辆的操控动力模型参数；Dong等[13]用随机子空间法识别车辆模态并计算车辆惯性参数变化，并提出较高的阻尼比（20%～30%）对随机子空间法的识别结果有较大的影响。Chen等[14]提出了基于平均相关函数的随机子空间算法（ASC-SSI），有效抑制噪声干扰且需处理的数据量小，适合结构在线状态监测。综合上述，本文提出一种监测方法，通过识别模态参数变化判断悬架弹簧刚度变化，对悬架系统进行在线状态监测。

1 数值模拟验证

1.1 平均相关随机子空间法基本原理

随机子空间算法（SSI）作为一种仅需响应数据的识别算法，不需要获取激励数据且适用于随机激励下的模态识别。利用对响应数据的协方差构成的矩阵进行奇异值分解，获得可控制矩阵和可观测矩阵，基于可观测矩阵的推移不变性计算状态矩阵，最终识别出模态参数。平均相关随机子空间法（ACS-SSI）采用多次平均后的相关函数信号取代原算法采用的响应信号作为算法输入，从而使其复杂工况下有更好的识别精度。在随机激励的模态识别中激振力一般是随机的，且与噪声很难区分，系统模型常被写成随机型离散状态空间方程：

式中：A——离散状态矩阵；

C——输出矩阵；

w（k）——随机输入并包含处理过程噪声；

ν（k）——测量噪声；

k——某离散时刻值。

状态矩阵A中包含系统信息，随机子空间法通过响应将状态矩阵A还原，并将其中的模态参数提取出来。假设由l个通道共同采集的l路测量信号组成的矩阵为y（t），在其中选择信噪比较好的一路信号，设为第k路信号的yk（t），可得所有原信号关于第k个通道的相关函数为

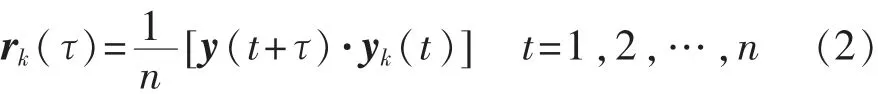
N为采集数据的总长度，τ=1，2，…，N-n，为相关函数的离散时间序列。相关函数rk（τ）∈Rl·τ为一个l路关于τ的一组相关函数信号。为使消噪效果更明显进行多组试验得到了多组信号rk1，rk2，…，rkn，对其取平均后得到平均相关函数，用代替原y（t）作为输入进行模态识别。

之后方法与协方差驱动的随机子空间方法相同[15]：用由的协方差构成矩阵T1|i，并对其进行奇异值分解（SVD），从而得到离散状态矩阵A，A特征值分解后得到特征值λi及特征向量Ψi，将其最终转化为固有频率fni、模态阻尼比ξi以及模态向量νi。

1.2 识别验证

由于高阻尼比对识别结果的影响，随机子空间法在阻尼比达到20%～30%的情况还较少被应用[13]。但是车辆悬架系统阻尼比较高，阻尼比最高的一阶一般超过20%～30%。为了验证改进后的平均相关子空间算法在高阻尼比下的可靠性，建立三自由度数值模拟系统如图1所示。系统中3个质量块m1、m2、m3由3个固定刚度k1、k2、k3的弹簧和阻尼器c1、c2、c3连接。因固有频率由质量和刚度共同决定，系统的固有频率不变，为fn1=2.5Hz，fn2=5.8Hz，fn3=9.9Hz。然后将不相关的3个低通滤波后的白噪声信号w1，w2，w3分别施加在3个质量块上模拟随机激励。设置不同的阻尼比如表1所示，共9次试验使阻尼比在2.5%～40%变化，观察对比随机子空间法（SSI）和平均相关随机子空间法（ACS-SSI）随阻尼比变化识别误差的变化情况。

设置采样频率为200Hz，采用奇异值突变结合稳态图定阶方法，并设置模态置信度（MAC）为30%，避免虚假模态被识别。设置仿真数据时长100 s，ACS-SSI进行50次平均。每个阻尼比进行10次蒙特卡洛试验，识别误差的均值由图2所示。

由于阻尼比对振动周期性的衰减随着阻尼的增大，识别结果的误差随之增大，但ACS-SSI始终优于SSI，尤其在阻尼比＞25%之后。对比在最高阻尼比（40%）下，ACS-SSI（3.9%）频率误差保持在SSI（8.7%）的一半以下；阻尼比误差ACS-SSI（29.3%）虽然低于SSI（42.4%），但是两者误差都过大而且很不稳定；对比模态向量误差，ACS-SSI（2.1%）和SSI（6.3%）的趋势基本与频率误差相一致并且稳定。由此可看出，ACS-SSI的识别结果明显优于SSI，尤其是频率和模态向量误差很小；阻尼比的识别虽有一些提升，但误差依然较大且不稳定。

图1 三质量振动模型

表1 算例阻尼比参数

图2 比较ACS-SSI和SSI的频率误差、阻尼比误差和模态向量误差均值

这是由于ACS-SSI使用多次平均后的相关函数（图3（a)）作为输入，相比原始加速度信号（图3（b）周期性更强），通过平均相关计算降低了原加速度响应信号中的随机成分。因此从二者的识别稳态图（图4）也可以看出，ACS-SSI的稳定性更强，识别结果更加收敛。

由此可以判断，在较高阻尼比的情况下，平均相关随机子空间法依旧适用且保持了相当的精度。模态频率和模态向量误差都较小，但是由于模态向量受车速和载荷影响较小，因此选择基于模态向量的方法进行状态监测。

2 模态仿真分析及识别

图3 SSI的输入信号和ACS-SSI的输入信号

图4 SSI和ACS-SSI稳态图

为了进一步研究基于ACS-SSI的悬架状态监控系统，建立七自由度的振动模型，用Simulink生成的四轮路面不平度时域信号输入到正常和故障模型中进行激励，最后利用得到的仿真响应信号进行模态识别，从而对弹簧故障进行仿真识别。图5为仿真分析过程示意图。

图5 仿真分析示意图

2.1 七自由度车辆振动模型

针对某车型乘用车建立七自由度整车振动模型（图6），由于运行时整车载荷不变将车身质量简化为m0和簧下质量（m1，m2，m3，m4）、悬架弹簧及减震器组成质弹阻模型。因仿真中车辆始终在较平坦的B级路面上直线行驶，将悬架弹簧刚度和减震器阻尼值分别线性化用k1，k2，k3，k4和c1，c2，c3，c4表示，轮胎刚度用kt1，kt2，kt3，kt4表示。

图6 七自由度车辆振动模型

根据某车型参数建立动力学平衡方程组，并整理为矩阵形式：

式中M、C、K分别是根据动力学微分方程整理得的质量阵、阻尼阵以及刚度阵。状态向量z=[z，θ，φ，z1，z2，z3，z4]T分别代表车身垂向位移、俯仰角、侧倾角及4个簧下质量位移，向量q=[q1，q2，q3，q4]T为路面输入的4个位移向量。

为方便仿真和识别，转化为状态空间模型。将式（3）通过式（4）变换为状态空间方程式：

2.2 模态分析

将状态矩阵A特征分解后可得到模态固有频率fn、阻尼比ξ以及模态向量ν。第i阶模态向量ν（i）为固有频率fni对应的特征向量，代表此模态频率下状态向量z=[z，θ，φ，z1，z2，z3，z4]T中各变量的振幅比。由表2看出，由于悬架是一个欠阻尼窄带低通系统，模态频率主要集中于低频，而所有阻尼比都超过了20%，俯仰和侧倾两阶阻尼比高达34%和38%。

表2 车辆模态频率及阻尼比

模态向量中的前3项（ν1，ν2，ν3）代表跳动、侧倾和俯仰（z，θ，φ）的振幅比，反映车身振动形态。为能直观表达，用式（6）将（ν1，ν2，ν3）投影到车身4个角，根据它们的振幅比（νa，νb，νc，νd）得到前三阶车身振型图（见图7）。代表车身跳动、侧倾和俯仰模态的振动形态，需要特别指出的是在理想的跳动和俯仰模态中不包含侧倾的运动，其左右两侧模态向量总是一致的。这也说明振型变化，尤其两侧振型的差异增大可以反映出车辆的故障情况。

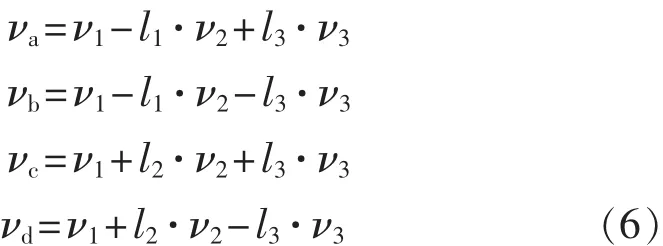
图7 车身模态振型

2.3 刚度变化对模态参数的影响

车辆在长期的运行过程中载荷状况、环境因素以及温度影响会造成悬架空簧失气、钢簧裂纹、钢簧断裂等故障，引起悬架的性能参数发生变化，如弹簧刚度的下降。为模拟故障以左后悬架为例，改变0%～50%左后悬架弹簧的刚度以模拟悬架参数变化，分析其对模态参数的影响。图8表示跳动模态和俯仰模态的固有频率fn1、fn3以及模态向量中的侧倾分量ν3（1）、ν3（3），其代表侧倾运动的占比。可以看出，两阶模态的频率随刚度降低而下降、侧倾模态向量的模随刚度下降从零开始增大，说明悬架发生故障会增加车身的侧倾振动。

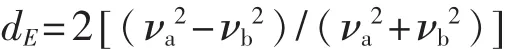
为了通过车身振型（νa，νb，νc，νd）表示侧倾振动成分的大小，通过式（7）计算左右振型大小的差异，dE为模态能量差异。由图9可以看出，跳动和俯仰两阶的模态能量差异随着某一悬架刚度下降都从零开始呈现明显上升趋势，因此模态能量差异可以作为悬架弹簧刚度变化进行诊断和监测的指标。

2.4 路面仿真激励及响应

为得到更接近真实的车辆振动信号，利用Simulink仿真生成四轮输入路面不平度时域信号。根据GB/T 7031——2005/ISO8608：11995《机械振动道路路面谱测量数据报告》的描述，将路面空间功率谱Gd（n）用以下拟合公式表示：

其中n为空间频率，m-1。根据国标n0=0.1m-1，为空间参考坐标；ω=2，为拟合功率谱密度指数。根据滤波白噪声法，可将空间频域式（8）转化为路面不平度的传递函数，将白噪声输入至传递函数组成的模块中，即可得到四轮位移时域信号，图10为Simulink仿真线框图。

车辆直线行驶时，同侧前后轮压过相同轮辙，所以其信号幅值相同但是后轮相位滞后Δt=l/u，l为前后轴轴距、u为车速。而左右轮辙功率谱密度曲线不同，它们之间的相干函数为

图8 模态频率及模态向量的模随刚度变化

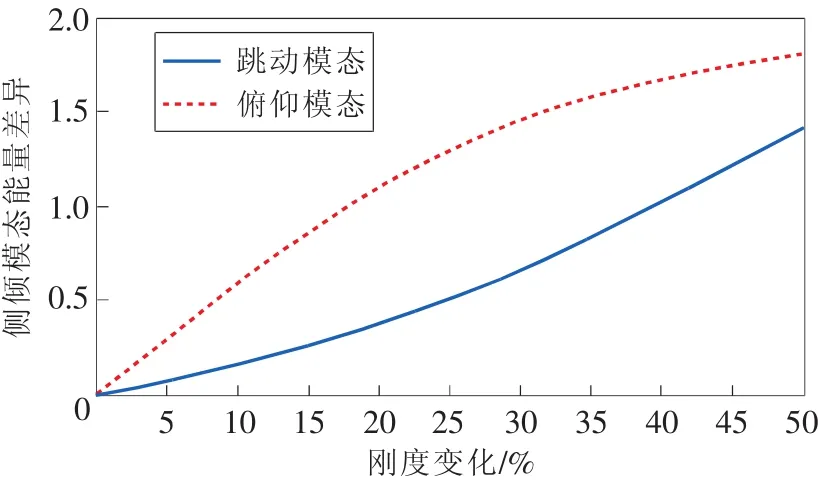
图9 模态能量差异随刚度变化

图10 路面仿真Simulink线框图

式（9）表示左右轮辙关系曲线。其低频段相关性高，高频段相关性低，使车辆收到的低频段左右两侧激励非常相似。这导致侧倾模态不能被激励出，所以2.3节未对侧倾模态进行讨论。为了模拟实车试验中的路面，设置模型中输入路面的粗糙度等级为B级。将路面不平度位移信号输入车辆振动模型后可得到车身振动信号，将车身垂向加速度、俯仰角加速度和侧倾角加速度3路信号进行变换后作为模态参数识别的输入变量。

2.5 仿真识别结果及误差分析

在选取的仿真响应信号中添加信噪比SNR=2的噪声信号，模拟带有测量噪声的真实测量信号。再进行平均相关子空间算法的模态识别，设置平均次数100次，每段数据时长为20 s，分别对左后悬架刚度为100%、90%、80%的3种状态进行识别和对比。

由于文中上述的侧倾激励有限等原因，仿真识别仅能识别出跳动和俯仰两阶模态，其误差均与数值模拟的结果相吻合，而且侧倾趋势也能被清晰的显示出来。为了观察是否能在现有误差基础上判断出故障，对3种状态分别进行50次蒙特卡洛重复实验，得到了3种状态下模态能量差异的分布图（见图11）。可以看出，由于误差影响，每次试验数值存在一定的波动，但10%的刚度变化造成的差异依然可以清晰地判断出来，说明将模态能量差异作为状态监测的判断故障依据是合理的。

图11 不同状态下模态能量差异

3 实车试验

为了验证以上模态识别结果以及基于振型及模态能量监测方法的可信度进行路上实车试验。

3.1 试验方案

选用某小型乘用车为试验用车，利用MEMS惯性传感器采集车身垂向加速度、俯仰角加速度和侧倾角加速度数据。对两种车况进行路上试验：1）原装悬架作为基线；2）将左后悬架弹簧更换为原弹簧80%刚度的弹簧以模拟悬架故障。

在正常路况下行驶，车速保持在30 km/h左右，每种车况运行60 km/h以上，并利用GPS统计里程和车速。路况由平整路况、少量减速带和小段不平整路段组成。将车身振动的功率谱密度与不同路面等级仿真车身功率谱密度比较获知，试验路面接近于B级标准路面。

3.2 传感器布置

针对车身的3个变量，选择MEMS惯性传感器测量。随着MEMS传感器技术发展，其不仅可以同时采集加速度和角速度信号而且还具有频率范围大、精度高和成本较低等优点。研究中选用的MPU-6050芯片量程达±16g，非线性＜0.5%。

将传感器布置在车底盘计算得到质心位置（见图12）。为减少噪声干扰和位置误差，经多个方案对比后选择将传感器用陶瓷胶粘在10mm厚的钢板上，再用螺栓将钢板固定在车底盘的车架上。为减小安装时的平行度误差增加轴间耦合，安装时需要保证传感器坐标系与车身坐标尽可能地保持平行，并对安装后的传感器进行侧倾和俯仰测试，确认X/Y的轴间耦合误差＜2%。

图12 传感器安装和布置

3.3 试验数据处理与结果分析

对试验数据进行预处理：首先为了排除非平稳车速对响应数据的干扰，剔除信号中纵向和横向加速度过大的信号段，以减小非匀速和非直线运动对识别结果的影响。再对信号进行截止频率为8Hz的低通滤波，去除发动机振动造成的影响（发动机工作转数为800～2000 r/min）。完成以上等处理后将信号分为100段，每段20 s，其他参数设置与仿真识别基本相同。其识别的固有频率及振型结果如图13所示。

图13（a）和图13（b）为基线状态下跳动和俯仰模态振型图，图13（c）和图13（d）为一弹簧为原弹簧80%刚度下跳动和俯仰模态振型图，从图中可以看出二者的基本振动形态相同，但从阵型计算结果来看故障状态的俯仰和侧倾姿态大于正常状态。

图13 基线状态与故障状态模态参数

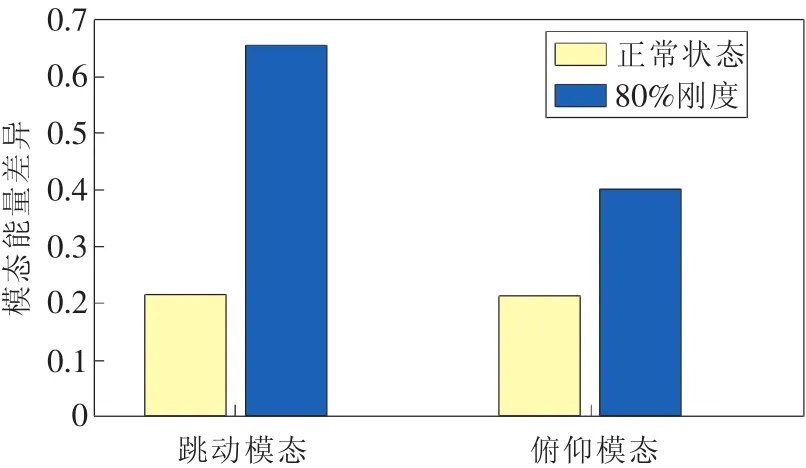
图14 正常与80%刚度的模态能量差异

为了更清晰地表达振型变化，求其模态能量差异，从图14可以看出，故障状态下模态能量差异明显大于基线状态。由此实验结果可得，基于模态识别的方法，通过振型及模态能量差异的变化可以对悬架状态进行在线监测。实际应用时可对不同的车辆和故障形式进行试验标定，以得到理想的监测效果。

4 结束语

本文通过研究平均相关随机子空间算法在较高阻尼比情况下的识别准确性，验证了该算法在悬架系统状态监测中的可行性。建立了一种利用识别模态参数变化的监测方案，并用实车实验验证了该方案的可信性。本文方法为悬架系统的在线状态监测和故障诊断提供了一种具有较高准确性与鲁棒性的方法。

[1]徐道临，张林，周加喜.重型矿用自卸车油气悬架参数优化[J].振动与冲击，2012，31（24）：98-101.

[2]王铁，高昱，申晋宪.水罐消防车操纵稳定性与平顺性的仿真优化[J].汽车工程，2012，34（12）：1114-1118.

[3]SCHUMANN A R，ANDERSON R J.Optimal control of an active anti roll suspension for an off-road utility vehicle using interconnected hydragas suspension units[J]. Vehicle System Dynamics，2003，37（1）：145-156.

[4]张慧杰，郭志平，司景萍，等.汽车悬架整车动力学模型的参数辨识[J].振动与冲击，2013，32（23）：145-150.

[5]HAYASHI Y，TSUNASHIMA H，MARUMO Y.Fault detection of railway vehicle suspension systems using multiple-model approach[J].Journal of Mechanical Systems for Transportation&Logistics，2008，1（1）：88-99.

[6]TSUNASHIMA H，MORI H.Condition monitoring of railway vehicle suspension using multiple model approach[J].Journal of Mechanical Systems for Transportation&Logistics，2010，7（3）：584-589.

[7]YIN S，LI X，GAO H，et al.Data-based techniques focused on modern industry：an overview[J].IEEE Transactions on Industrial Electronics，2015，62（1）：657-667.

[8]WEI X，LIN S，LIU H.Distributed fault detection observer for rail vehicle suspension systems[C]∥Control and Decision Conference，2012：366-383.

[9]YIN S，HUANG Z.Performance monitoring for vehicle suspension system via fuzzy positivistic C-means clustering based on accelerometer measurements[J].IEEEAsme Transactions on Mechatronics，2015，20（5）：1-8.

[10]GAO C，ZHAO Q，DUAN G.Robust actuator fault diagnosis scheme for satellite attitude control systems[J]. Journal of the Franklin Institute，2013，350（9）：2560-2580.

[11]HAYASHI Y，TSUNASHIMA H，MARUMO Y.Fault detection of railway vehicle suspension systems using multiple-model approach[J].Journal of Mechanical Systems for Transportation&Logistics，2008，1（1）：88-99.

[12]YUAN.Application of subspace-based method in vehicle handling dynamic model identification and properties estimation[J].International Journal of Vehicle Design，2011，56（1-4）：125-145.

[13]DONG G，CHEN J，ZHANG N.Investigation into onroad vehicle parameter identification based on subspace methods[J].Journal of Sound&Vibration，2014，333（24）：6760-6779.

[14]CHEN Z，WANG T，GU F，et al.The average correlation signal based stochastic subspace identification for the online modal analysis of a dump truck frame[J]. Journal of Vibroengineering，2015，17（4）：1971-1988.

[15]OVERSCHEE P V，MOOR B D.Subspace identification for linear systems：Theory[M].NewYork：Kluwer Academic Publishers，2012：149-157.

（编辑：李妮）

Research of method and test for suspension system condition monitoring based on modal parameter identification

LIMiaoshuo1，GU Fengshou2，WANG Tie1，LI Guoxing1，2，WANG Yonghong3，LU Xingchen1
（1.Department of Vehicle Engineering，Taiyuan University of Technology，Taiyuan 030024，China；2.Centre for Efficiency and Performance Engineering，University of Huddersfield，Manchester HD1 3DH，UK；3.Shanxi Dayun Automobile Manufacture Co.，Ltd.，Yuncheng 044000，China）

The performance of suspension system is directly related to the vehicle safety，riding comfort and handling stability.However，the road surface is a kind of random excitation，which places many difficulties in research on the condition monitoring of suspension system.Based on the average correlation signal based stochastic subspace identification（ASC-SSI），a novel method was presented to identify the modal parameters of suspension system in this article.The average correlation signal based stochastic subspace identification method was used to identify model parameters and the changes in suspension stiffness caused by changes of model parameters are monitored.Firstly，the validation of this algorithm was confirmed in a high damping ratio situation. Then，based on an established seven degree of freedom dynamic model，the modal parameters of suspension system were identified to analyze the influences of excitation from road roughness and strong noise to identification results，and then a monitoring method based on mode shape and modal energy was proposed.Finally，a test scheme using 9-axis MEMS inertial sensor was designed to monitor the normal and faulty condition and verify the validity and feasibility of the proposed method.

modal parameter identification；suspension system；average correlation signal based stochastic subspace identification；condition monitoring；MEMS

A

1674-5124（2017）05-0138-07

10.11857/j.issn.1674-5124.2017.05.029

2016-10-07；

2016-12-05

李苗硕（1988-），男，山西太原市人，硕士研究生，专业方向为车辆现代设计理论。