底盘测功机运转中内生摩擦阻力的补偿数模研究

欧阳爱国，卢晋夫，刘燕德，王均刚，毕鹏飞

（华东交通大学机电与车辆工程学院，江西 南昌 330013）

底盘测功机运转中内生摩擦阻力的补偿数模研究

欧阳爱国，卢晋夫，刘燕德，王均刚，毕鹏飞

（华东交通大学机电与车辆工程学院，江西 南昌 330013）

为解决滚筒底盘测功机运转过程中因内生摩擦阻力损耗而使测功装置显示数值偏小的问题，给其数值补偿提供理论依据。根据能量守恒原理，通过二次加载滑行和无加载滑行等实验得到相关测试数据，建立单滚筒底盘测功机无车辆运转中内生摩擦阻力的数学模型，以AVL Roadsim 48″单滚筒底盘测功机为试验机，实验测得其在速度20，40，60，80，100 km/h下的内生摩擦阻力值与数学模型计算值的误差≤10.47%。研究表明：滚筒底盘测功机的内生摩擦阻力可通过二次加载力值及二次加载和空载下的滑行距离获得，其内生摩擦阻力大小随速度的增大而增大，常规速度下空气产生的摩擦阻力远小于其机械阻力。

底盘测功机；内生摩擦阻力；数学模型；滑行测试

0 引言

底盘测功机是一种汽车底盘综合性能检测设备，主要由滚筒装置、测功装置、飞轮机构、测速机构、控制与指示装置、电动机及发电机等构成[1]，其主要功能是测试汽车的驱动轮输出功率、加速性能、滑行能力和传动系统的传动效率，间接可测试发动机功率、汽车燃油经济性能和废气排放性能[2]。

底盘测功机运转测试过程中，内部相对运动零部件间会产生摩擦而消耗能量，如滚筒自身转动部分的损耗、轴承摩擦和其他功率吸收装置的阻力等[3]，其大小会随机器磨损变形而变化，影响底盘测功机的模拟加载，使底盘测功机动力吸收装置的记录数值不准确[4-5]，如能将底盘测功机的内生摩擦阻力准确计入以抵消摩擦阻力对试验结果的影响，则能大大提高底盘测功机的检测精度。

本文拟针对滚筒底盘测功机运转过程中因内生摩擦阻力损耗而使测功装置显示数值偏小的问题，根据能量守恒原理，通过二次加载滑行法和无加载滑行法等试验获得相关测试数据，建立滚筒底盘测功机的内生摩擦阻力数学模型，并对其进行算例分析和实验验证，为底盘测功机运转过程中测功装置的数据进行数值补偿提供理论依据。

1 底盘测功机转动中的摩阻分析

1.1 底盘测功机的车辆检测精度分析

底盘测功机的车辆检测一般是在室内利用滚筒模拟路面，让汽车在滚筒上运行时所受到的阻力等同于它在路面上行驶所受到的阻力，从而达到试车场的测试效果。检测车辆时，车辆在底盘测功机上所受的阻力主要有：测功机的摩擦阻力、测功机加载阻力、汽车传动系摩擦阻力、车轮与滚筒间的滚滑阻力及惯性阻力[6-7]。其中底盘测功机运转过程中本身的摩擦阻力不可忽略，其会加大底盘测功机的加载阻力，造成被测车辆所受阻力大于在实际道路上的所受阻力，从而难以准确地模拟道路行驶工况，影响车辆检测的准确度。

1.2 摩擦阻力构成因素分析

底盘测功机运行时内部摩擦阻力的构成非常复杂，它主要包括滚筒自身转动时的阻力、滚筒两侧轴承产生的摩擦阻力、联轴器摩擦阻力及电力测功机在运行时自身的阻力等运动过程中形成的机械摩擦阻力[8-9]。机械摩阻大小随滚筒转速的增加而增大，一般与速度呈线性关系，其关系式为F1=a+bν；另外，在底盘测功机的运行过程中，运动部件快速运转时也会与空气产生摩擦而形成空气阻力，由于测功过程中滚筒运行速度快，因此这一部分阻力也不可忽略，其大小可表示为F2=kν2，即底盘测功机运转时的摩擦阻力可被看成是机械阻力与空气阻力之和，其与滚筒速度的关系式[10]可表示为F=A+Bν+Cν2。由于摩擦阻力构成的复杂性，要确定该关系式的系数A、B、C，单纯从理论上推导是难以获得的，需要通过理论与试验相结合，检测速度点的相关数据推导出摩擦阻力的数学模型，利用数据拟合方法，得到底盘测功机实测过程中其摩擦阻力造成损失的补偿关系。

2 内生摩擦阻力的数模构建

式中：Fν0——单滚筒底盘测功机在待测速度ν0时的内生摩擦阻力；

Sν0——单滚筒底盘测功机所有转动部件的总转动惯量的当量质量在滑行中相当的平均滑动距离；

M——单滚筒底盘测功机所有转动部件在滑行过程中总转动惯量的当量质量。

式（1）中除了M为未知量，其他3项Sν0、ν1、ν2均可通过滑行实验得出，即欲获得Fν0，须先求出M。为此，本文采用对单滚筒底盘测功机进行二次加载滑行的方法来获得M。

二次加载滑行法是通过对底盘测功机进行两次不同的加载，让底盘测功机在没有车辆时滑行进行的检测[12-13]。单滚筒底盘测功机第1次开始运行前，先给它加载一个阻力值F1，然后让单滚筒底盘测功机在加载力F1和内生摩擦阻力的共同作用下滑行，选取其运行开始时的速度点ν1和结束时的速度点ν2，记录这段滑行的时间t1及滑行的距离S1，结束第1次加载运行；然后进行第2次加载运行开始前，先给单滚筒底盘测功机加载一个大小不同于F1的加载力F2，然后让单滚筒底盘测功机在加载力F2和内生摩擦阻力的共同作用下滑行，并保证其开始时和结束时的速度值与第1次运行时的一样，仍然为ν1和ν2，记录第2次加载滑行的时间t2及滑行的距离S2。由于速度ν1和ν2与ν0接近，这3种速度运行时的单滚筒底盘测功机产生的摩擦阻力可近似看成相等，利用能量守恒原理可建立以下数学模型：

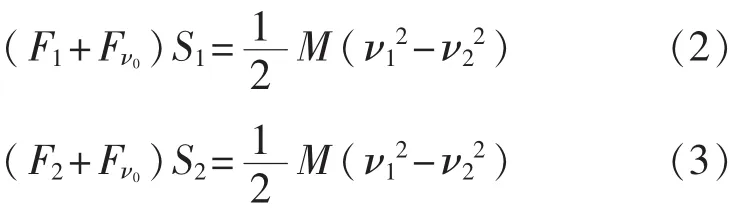
式中：F1——第1次加载运行时单滚筒底盘测功机的加载力；

F2——第2次加载运行时单滚筒底盘测功机的加载力。

联解式（2）、式（3）可得：

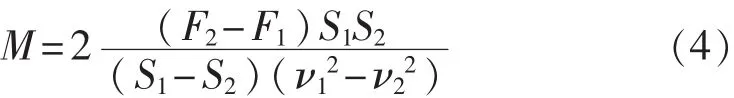
将M代入式（1）即可求出单滚筒底盘测功机在待测速度ν0时的内生摩擦阻力Fν0。

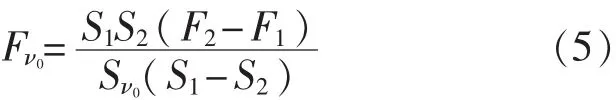
3 算例分析

以AVL公司生产的型号为AVL Roadsim 48″单滚筒底盘测功机为例，选取测试速度点ν0=110km/h，空车开动底盘测功机热机至热平衡状态，进行二次加载滑行，二次加载载荷分别为100N和200N；开始和结束测试时的速度分别为ν1=120 km/h和ν2= 100 km/h，二次加载滑行的测得时间分别为39.03 s和27.01s；二次加载滑行的测得距离分别为1691m和964m。然后再让电机带动单滚筒底盘测功机进行无车无加载滑行，开始和结束测试的速度点同样分别选为ν1=120 km/h和ν2=100km/h，可测得无加载滑行的滑行时间为64.62 s，滑行距离为5967m；将上述测试数据代入Fν0表达式可得速度ν0=110 km/h时单滚筒底盘测功机的内生摩擦阻力Fν0=37.58N。按上述同样方法，在空载滑行和二次加载F1=100N和F2=200N下滑行，其他速度点（如20，40，60，80，100km/h）的单滚筒底盘测功机内生摩擦阻力相关情况见表1。

表1 不同速度点的内生摩擦阻力

利用表中数据进行其多项式拟合，可建立其曲线表达式为

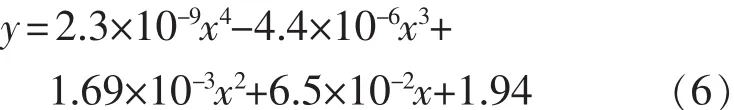
式中：x——速度；

y——单滚筒底盘测功机内生摩擦阻力。

由式（6）可知x4和x3的系数相对x2的系数来说很小，即速度的3次方和4次方对单滚筒底盘测功机内生摩擦阻力影响很小，因此单滚筒底盘测功机的速度与其内生摩擦阻力的关系可近似看成为一条抛物线关系，其表达式为

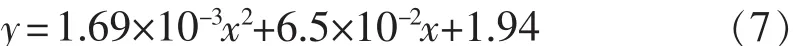
式中x2的系数相对x项和常数项较小，说明单滚筒底盘测功机空气阻力的影响相对其机械阻力的影响较小；x的系数相对常数项较小，说明单滚筒底盘测功机的机械阻力起点较高，固有机械阻力较大。

4 试验验证

将AVL公司生产的型号为AVL Roadsim 48″单滚筒底盘测功机的电涡流测功器与变速器之间的连接装置断开，由带动单滚筒底盘测功机空载运转的电机直接驱动电涡流测功器运转，选取验证速度区间16～128 km/h，以16 km/h为速度间隔，在每个速度点测试时，对电涡流测功器加载，直至其运转速度稳定，则所加载荷即为单滚筒底盘测功机在该速度点的内生摩擦阻力值，然后再至下一速度点，按此方法获取在各测试速度点的内生摩擦阻力值，最后将获取的结果与空车滑行数学模型计算得到的内生摩擦阻力进行比较，其结果如表2。

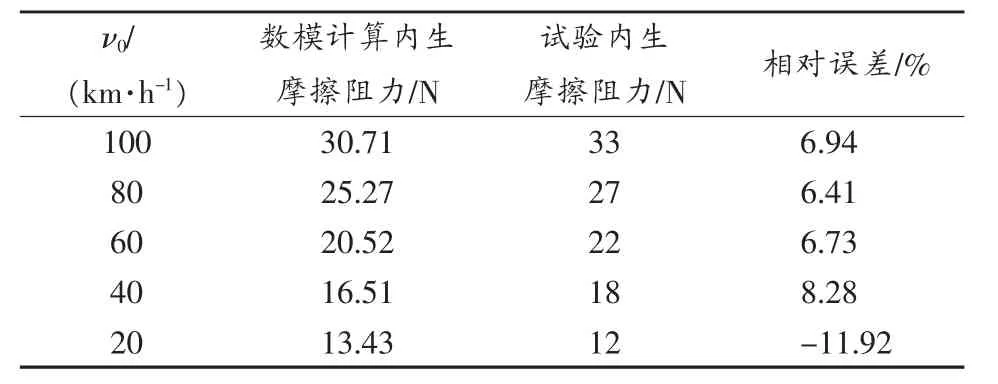
表2 试验和数模计算的内生摩擦阻力比较

相对误差以试验验证得到的内生摩阻为标准计算获得。可以看出，数模计算的单滚筒底盘测功机内生摩阻与试验验证的相差较小，变化规律一致，单滚筒底盘测功机的速度为ν0=80 km/h时的内生摩阻的相对误差最小，说明本文所建立的单滚筒底盘测功机内生摩擦阻力的数学模型基本能反映其实际情况。

5 结束语

1）在单滚筒底盘测功机上进行无车状态下的无加载滑行和二次加载滑行，通过测量无加载滑行的滑行距离Sν0及在两次加载F1和F2下的滑行距离S1和S2，即可获得滚筒底盘测功机的内生摩擦阻力Fν0，其数学关系模型为

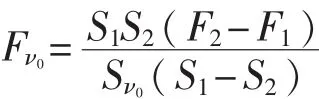
2）型号为AVL Roadsim 48″单滚筒底盘测功机的内生摩擦阻力Fν0与其速度之间存在抛物线关系，其关系式可近似表达为

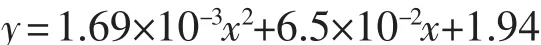
3）滚筒底盘测功机的内生摩擦阻力随速度的增加而增大，其中机械阻力比空气阻力对滚筒底盘测功机的影响更大，且机械阻力的起点较高。

[1]王晓东.底盘测功机模拟车辆道路行驶阻力加载力研究[D].西安：长安大学，2010.

[2]王娜.HYCG-10A型底盘测功机测试性能改进[D].哈尔滨：哈尔滨工程大学，2007.

[3]龚志远，刘志雄，欧阳爱国，等.单滚筒底盘测功机寄生摩擦阻力测量方法研究[J].中国测试，2016，42（6）：5-8.

[4]刘磊.基于底盘测功机台架系统阻力测试方法研究[D].长春：吉林大学，2012.

[5]CHELIF，BRAGHIN F，BRUSAROSCO M，et al.Design and testing of an innovative measurement device foe tyre-road contact forces[J].Mechanical Systems and Signal Processing，2011，25（6）：1956-1972.

[6]任礼行，刘青.轮胎滚动阻力测量与分析[J].汽车工程，2000，22（2）：13-16.

[7]GROVER P S.Modeling of rolling resistance test data[J]. Powder Technology，2011（3）：269-282.

[8]田颖，金振华，聂圣芳.交流电力测功机控制系统的研究[J].汽车工程，2014，36（1）：125－128．

[9]王建强，戴建国，高蔚.台试轮胎滚动阻力模型应用研究[J].农业机械学报，2003，34（4）：35-38.

[10]张绍国，高峰，杭柏林，等.汽车轮胎滚动阻力试验机测试方法分析[J].中国公路学报，2012，25（1）：146-151.

[11]欧阳爱国，肖文龙，陈齐平.单滚筒底盘测功机对轮胎滚动阻力测定的精准度研究[J].中国测试，2015，41（8）：13-16.

[12]欧阳爱国，毕朋飞，肖文龙，等.轮胎滚动阻力精确测试方法研究[J].中国测试，2015，41（12）：16-19.

[13]何建，杨波.汽车底盘测功机阻力设定及其典型问题分析[J].轻型汽车技术，2008,9（3）：20-22.

（编辑：李妮）

Research on mathematical model of com pensation for internal friction resistance of chassis dynamometer in operation

OUYANG Aiguo，LU Jinfu，LIU Yande，WANG Jungang，BI Pengfei
（School of Mechatronics and Vehicle Engineering，East China Jiaotong University，Nanchang 330013，China）

In order to solve the problem that the display value on power testing device was small because of the internal frictional resistance loss in the process of operation of a drum chassis dynamometer and provide theoretical basis for its value compensation.The mathematical model of the internal frictional resistance of a single-drum chassis dynamometer in the operation was established through the test data obtained in the experiment method of the secondary load sliding and the no-load sliding and other related method according to the principle of conservation of energy.The experimental value of internal frictional resistance of a single-drum chassis dynamometer AVL Roadsim 48″(test device)was obtained at the speed of 20，40，60，80，100km∕h and the error between it and the calculating value of mathematical model was less than or equal to 10.47%.The results show that the internal frictional resistance of a drum chassis dynamometer can be obtained by the secondary load value and the sliding distance under secondary load and no-load，and the value of the internal frictional resistance increases with speed，and the friction resistance produced by the air under conventional speed is far less than its mechanical resistance.

chassis dynamometer；internal frictional resistance；mathematical model；slide test

A

1674-5124（2017）05-0124-03

10.11857/j.issn.1674-5124.2017.05.026

2016-10-15；

2016-12-08

国家自然科学基金项目（51265015）；江西省自然科学基金项目（20161BAB206153）；江西省研究生创新专项资金项目（YC2016－S255）；华东交通大学科研启动基金资助项目（26441039）

欧阳爱国（1968-），男，江西南昌市人，教授，硕士生导师，主要从事车辆性能检测和现代传感器测试技术。