基于EEMD能量熵的高速列车蛇行诊断研究

刘棋，宁静，叶运广，陈春俊

（西南交通大学机械工程学院，四川 成都 610031）

基于EEMD能量熵的高速列车蛇行诊断研究

刘棋，宁静，叶运广，陈春俊

（西南交通大学机械工程学院，四川 成都 610031）

为解决列车高速运行时，出现的蛇行失稳故障难以被准确识别的问题，提出一种基于集合经验模态分解（ensemble empirical mode decomposition，EEMD）熵特征和最小二乘法支持向量机（least squares support vector machine，LSSVM）的高速列车蛇行异常运动状态的诊断方法。首先通过EEMD对高速列车蛇行故障振动信号进行分解，再提取固有模态函数（intrinsic mode function，IMF）分量的样本熵特征、香农熵特征和能量熵特征，最后分别用LSSVM进行训练和识别。试验结果表明：高速列车在330～350km/h的运行速度下，EEMD熵特征-LSSVM方法能准确识别高速列车蛇行失稳状态，并且LSSVM的输入特征为能量熵特征时，识别效果优于样本熵特征和香农熵特征，识别率达到95%。

蛇行失稳；集合经验模态分解；固有模态函数；熵特征；最小二乘法支持向量机

0 引言

列车绕着轨道中心线一边横移一边摇头向前耦合运动，即蛇行运动[1]。蛇行运动的最大特点就是它的振动频率随着车辆运行速度的增大而增大，而车辆系统的自振频率与车辆运行速度是基本无关的，这样在某个速度段，蛇行运动频率就有可能和车辆系统的某个自振频率接近，从而产生共振[2]。当列车发生蛇行运动，若车辆运行速度不高，蛇行运动频率低于车辆自振频率时，列车车体、构架、转向架的蛇行运动各振型的幅值会不断减小，即蛇行运动收敛，此时，车辆的蛇行运动是稳定的，且幅值衰减越快，稳定的程度就越高。若车辆以较高的速度运行，蛇行运动频率与车辆自振频率接近时，其振幅不断的增大，那么这时的蛇行运动就丧失了稳定性，即发生了蛇行失稳，且幅值增大越快，失稳的程度就越严重[3]。

国内外学者从动力学角度对高速列车蛇行稳定性进行了研究，并取得大量成果[4-6]，但如何通过监测数据对蛇行失稳异常运动进行实时监测，国内外研究不多。传统的蛇行失稳分析方法通过观察取得加速度较大的数据段，对其峰值进行分析，但这种分析方法效率极低，难以监测整个数据段；或者通过FFT对整个数据段进行频谱分析，但得到的复杂频率成分掩盖了很多问题[7]。为克服这些问题，文献[8]结合多重分形与SVM方法识别高速列车运行状态，文献[9]应用EEMD和球SVM方法对高速列车转向架故障进行了分析，但都未能反映列车运行时的蛇行运动信息特征，并且采用的数据都是实验仿真数据，而非实际运行数据。

高速列车在运行时，振动特性极为复杂，其信号往往是非平稳的，同时夹杂着冲击信号，EEMD具有自适应性和抑制模态混叠的作用，在处理此类信号时有着独特的优势[10]。同时EEMD分解后的IMF分量的样本熵、信息熵、能量熵分布有所差异[11-13]。因此，本文提出了一种适用于高速列车蛇行异常诊断识别的方法，具体信号处理步骤如图1所示。

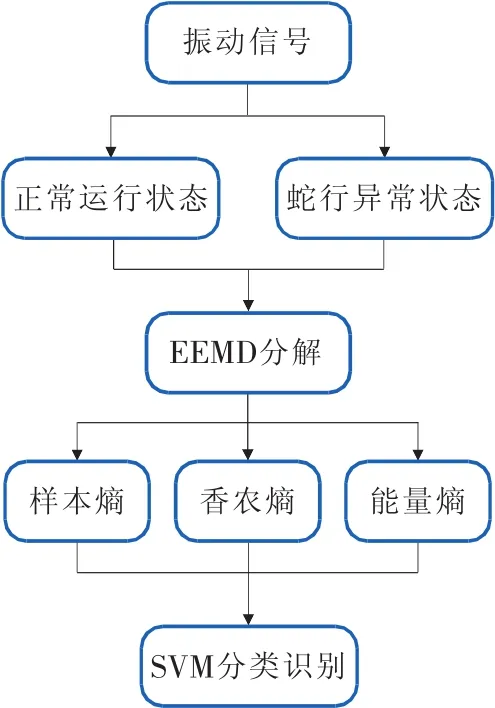
图1 信号处理流程图

1 试验工况

该次试验以某高速列车动车组为研究对象，测试路线为沪杭线。为了准确识别出高速列车蛇行运动状态，需对转向架构架的横向振动规律进行检测[14]。为提高检测数据的可信度，把振动传感器安装在转向架构架的对角上，如图2所示，两个传感器对转向架同时进行检测，并行对比[15]。

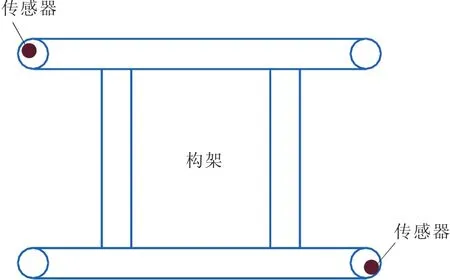
图2 转向架传感器安装示意图

据TB/T 3188——2007《铁道客车行车安全监测诊断系统技术条件》[15]，当转向架构架横向振动加速度峰值连续6次以上达到或者超过极限值8～10m/s2（与转向架的设计相适应）时，即判定为蛇行失稳。按照此标准，当高速列车时速在330～350 km/h发生蛇行异常故障时，分别筛选正常运行和蛇行异常两种工况下的数据段进行分析。

2 EEMD简介

列车运行时，系统振动是速度、里程、轨道等多种因素相互作用的结果，存在复杂的非线性关系，其振动信号属于非平稳信号。当列车发生蛇行故障时，其信号包含有各种冲击成分，为有效抑制EMD分解中出现的模态混叠现象，Huang等[16-17]提出了EEMD解决这一问题。

EEMD的本质是将信号中不同尺度的波动或者趋势逐级分解开来，得到一系列具有不同尺度的真实物理意义的IMF分量[18]。

EEMD步骤如下：

1）向信号加入正态分布白噪声nω（t）。

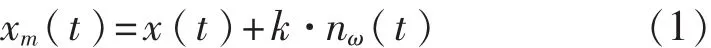
式中k为加入白噪声的幅值系数。

2）对信号xm（t）进行EMD分解，得出一组IMF分量ci，m。

3）m值从1取到n，重复1）、2），每次加入新的白噪声序列，分解出n组IMF分量序列{ci，m}。

4）将n组IMF分量{ci，m}的集成均值作为最终结果。

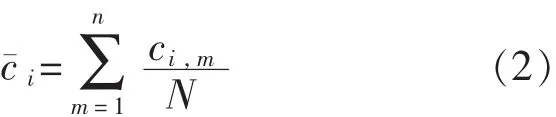
式中：N——EMD的集成次数；

ci，m——第m次EMD所产生的第i个IMF分量。

3 相关特征提取

3.1 样本熵

样本熵是用来刻画时间序列复杂度的一种度量方法，其与时间序列复杂度有着正相应关系，序列复杂度越高，其值就越大；熵值越小，序列的自我相似度越高[11]。列车运行时，其处于不断振动的状态，用EEMD对振动信号进行分解，各阶IMF分量复杂度必然不同，其样本熵值不同。所以理论上采用样本熵作为识别蛇行运动的特征是一种有效的方法。

对于一个时间序列{x（i）|1≤i≤N}的样本熵的计算步骤如下：

1）预先选定模式维数m构造一组m维矢量X（i）。

2）定义矢量Xm（i）与Xm（j）间的距离d[Xm（i），Xm（j）]表示，则：

3）给定阈值r，求取小于r的距离d[Xm（i），Xm（j）]的数目与矢量总个数N-m比值，记为Bim（r），即：

其中i=1，2，3，…，N-m+1，i≠j。

4）将模式构成一组m+1维矢量，重复2）和3），得到：

5）理论上此序列的样本熵为

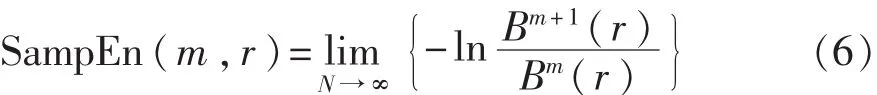
当N为有限值时，按照上述步骤得出的时间序列样本熵的估计值为

3.2 香农熵

香农熵又称为信息熵，通过随机系统的统计特性，反应系统的内部信息。某种事件发生的可能性越大，系统越稳定，香农熵值越小；反之，系统越紊乱，香农熵值越大[19]。

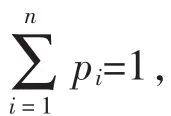
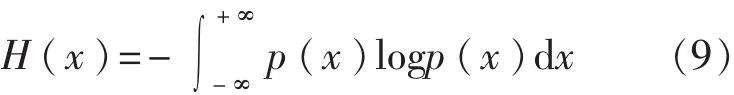
3.3 能量熵

振动信号通过EEMD分解后，得到的各阶IMF分量可以反映频段信息。利用IMF能量熵分布特征，可以有效地揭示高速列车蛇行异常状态。

第i阶IMF能量熵计算步骤：

1）对信号进行预处理，然后进行EEMD分解，得到各阶IMF分量ci（t）。

2）选取适当的IMF分量，计算其IMF分量的能量。

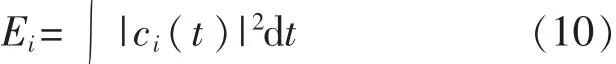
式中pi=Ei/E，即i阶IMF能量与总能量比值。

4 LSSVM

标准SVM训练样本时需要求解二次规划问题，训练速度较慢。文献[20]提出一种新的SVM（LSSVM）方法，其通过求解线性方程组代替求解二次规划问题，避免了不敏感损失函数，大大降低了计算复杂度，提高了运算效率。

其优化问题可表示为

其中，i=1，2，…，n，x是输入矢量，ω是可调的权值矢量，b是偏置，ξi为松弛变量，并且ξi＞0，可以度量一个数据点对模式可分的理想条件下的偏离程度，λ是平衡最小分类边界和最小分类误差的惩罚因子，非线性变换φ（x）将给定输入样本x映射到更高维的特征空间。

可以推得，最优超平面的分类决策函数为

式中K（xi·x）为满足Mercer定理的核函数。

5 试验数据处理与分析

由于蛇行运动的振动频率在2～12.07Hz范围内[10]，根据香农采样定理和经验选取采样频率为250Hz，再对采集的信号进行2～12.07Hz带通滤波处理。按照文献[8]中“当转向架构架横向振动加速度峰值连续6次以上达到或者超过极限值8～10m/s2”这一标准，分别观察筛选蛇行异常和正常两种工况各60组数据，每组数据长度1000。

5.1 信号的EEMD分解

对筛选得到的振动信号分别进行EEMD信号分解，得到结果如图3所示，其中同种状态分解结果相似，不同状态差异明显，由于篇幅所限，只列出蛇行异常振动信号EEMD分解结果。

5.2 相关特征提取

经EEMD分解后的IMF分量为不同的平稳信号，在蛇行异常和正常状态下，各阶IMF包含的样本熵、香农熵、能量熵特征有所区别，因此拟选取IMF分量的样本熵、香农熵、能量熵特征来识别蛇行异常和正常状态。具体步骤如下：

1）对原始信号进行EEMD分解，为保证后续性选取包含主要信息的前6阶IMF分量。

2）取各IMF分量的样本熵、香农熵、能量熵特征，分别构造相关特征向量。由于EEMD是一种主成分提取方法，分解结果中前几个分量包含了信号的主要信息，且实验所得IMF分量个数都大于6，因此利用前6个分量求取熵值。实验表明，高速列车在正常运行和蛇行异常两种工况下，同一工况的特征向量相似，不同工况下的特征向量差异明显，其中能量熵特征差异尤为明显。如表1所示，其中针对两种状态特征差异，EEMD能量熵最大，EEMD样本熵次之，EEMD香农熵最小，由于篇幅限制，分别只给出2组样本的特征值。

6 LSSVM训练与测试

表1 正常运行和蛇行异常下相应IMF熵特征

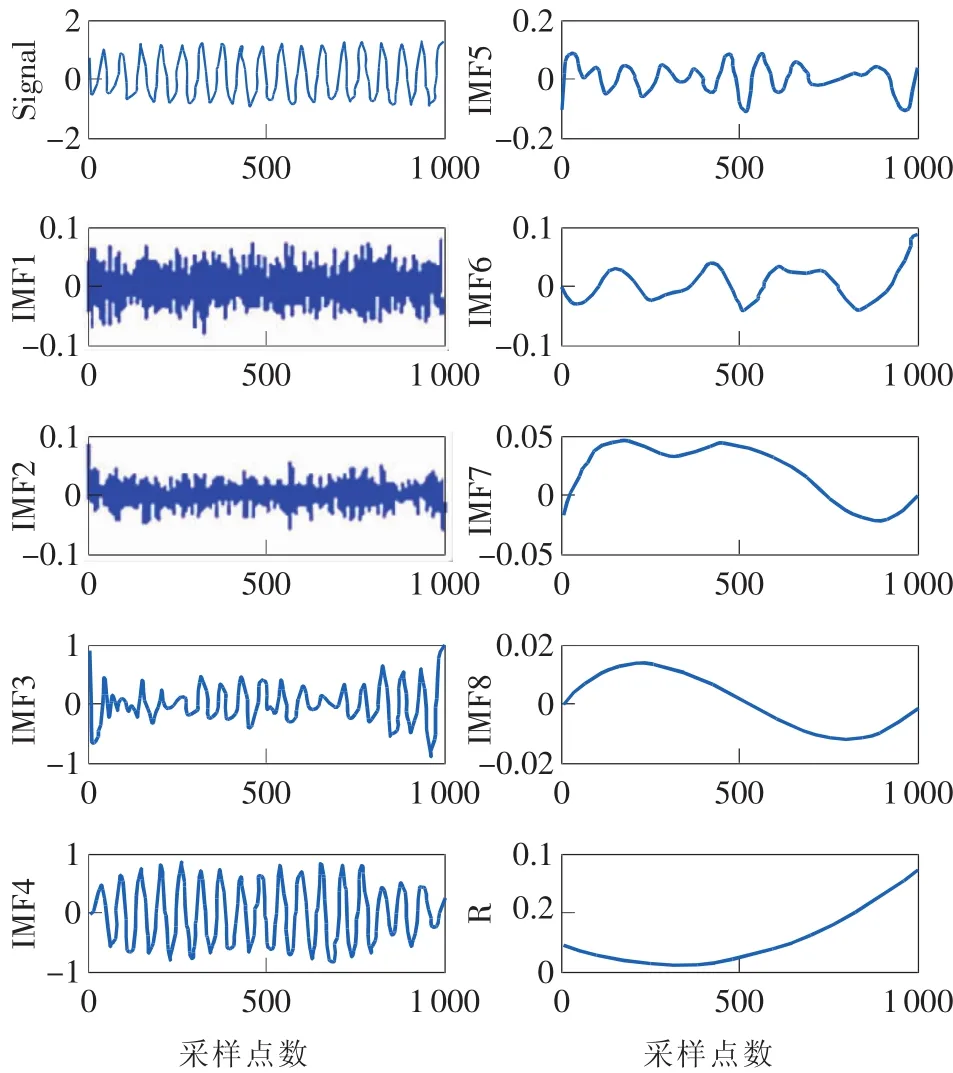
图3 蛇行异常振动信号EEMD分解结果

表2 训练LSSVM期望输出值

将训练样本划分为两类，t=1和t=0，分别代表高速列车正常运行状态和蛇行异常状态。按照5.2提取样本熵、香农熵、能量熵特征作为LSSVM的输入。分别采用60组（30组正常，30组蛇行异常）样本作为训练。表2为训练LSSVM期望输出，其中3种方法正常运行状态输出期望值都设为1，蛇行异常状态输出期望值都为0。

训练完成后，用60组（30组正常，30组蛇行异常）样本作为测试，识别结果如表3所示。通过比较得知，采用能量熵作为LSSVM输入特征的方法效果最好，其次是样本熵，最后是香农熵。

表3 正常运行和蛇行异常状态下LSSVM的正确识别结果

7 结束语

针对蛇行失稳这一故障，本文从数据监测角度出发，结合EEMD和样本熵、信息熵、能量熵特征以及LSSVM来诊断高速列车运行过程中的蛇行失稳故障。通过EEMD对振动信号进行分解，求得IMF分量的样本熵、香农熵、能量熵特征，分别作为LSSVM的输入进行训练和测试，最后数据处理结果表明：

1）EEMD样本熵、香农熵、能量熵特征和LSSVM结合方法都能成功识别高速列车正常运行和蛇行异常状态。

2）EEMD-LSSVM能准确识别高速列车蛇行异常状态，并且提取IMF分量的能量熵特征作为LSSVM的输入特征时，故障识别率最高，识别率达95%，其次是样本熵特征，识别率为86.67%，最后是香农熵特征，识别率为78.33%。

[1]DE-PATER A D.The approximate determination of the hunting movement of a railway vehicle by aid of the method of krylov and bogoljubow[J].Applied Scientific Research，1961，10（1）：205-228.

[2]刘峰，延九磊，董孝卿，等.转向架横向稳定性的实时在线监测[J].铁道机车车辆，2010，30（2）：5-8.

[3]池茂儒，张卫华，曾京，等.蛇行运动对铁道车辆平稳性的影响[J].振动工程学报，2008，21（6）：639-643.

[4]OKAMOTO H，KOTANIM，LIN S，et al.Stabilization control for hunting motion of railway vehicle by gyroscopic damper（experimental analysis using 1/10 scale vehicle model）[J].Transactions of the Japan Society of Mechanical Engineers C，2008，74（2）：235-241.

[5]MOHAMMADI A K，ALI N A.Effects of non-linear suspension on hunting and critical velocity of railway wheelset[J].International Journal of Advanced Design and Manufacturing Technology，2013，6（2）：51-59.

[6]罗仁，曾京.列车系统蛇行运动稳定性分析及其与单车模型的比较[J].机械工程学报，2008，44（4）：184-187.

[7]方松.高速铁路客车振动特性研究[D].成都：西南交通大学，2012.

[8]孙永奎，余志斌，金炜东.基于多重分形与SVM的高速列车运行状态识别方法[J].西南交通大学学报，2015，50（1）：7-12.

[9]翟冰，金炜东，秦娜.基于EEMD和球SVM的高速列车转向架故障估计[J].计算机测量与控制，2014，22（8）：2356-2359.

[10]WU Z H，HUANG N.Ensemble empirical mode decomposition：A noise assisted data analysis method[J]. Advances in Adaptive Data Analys，2009，1（1）：1-41.

[11]RICHMAN J S，MOORMAN J R.Physiological timeseries analysis using approximate entropy and sample entropy[J].American Journal of Physiology Heart and Circulatory Physiology，2000，278（6）：2039-2049.

[12]李亦农，李梅.信息论基础教程[M].北京：北京邮电大学出版社，2005：71-78.

[13]YANG Y,YU D J，CHENG J S.A rolling fault diagnosis method based on EMD energy entropy and ANN[J]. Journal of Sound and Vibration，2006，294（1/2）：269-277.

[14]ZHAIW，WANG K.Lateral hunting stability of railway vehicles running on elastic track structures[J].American Society of Mechanical Engineers，2010，5（4）：1-9.

[15]中华人民共和国铁道部.铁道客车行车安全监测诊断系统技术条件：TB/T 3188-2007[S].北京：中国铁道出版社，2007.

[16]HUANG N E，SHEN Z，LONG S R.The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J].Proc Royal Soc London A，1998，454（1971）：903-995.

[17]宁静，诸昌钤，张兵.基于EMD和Cohen核的轨道不平顺信号分析方法[J].振动与冲击，2013，32(4)：31-38.

[18]SUYKENS J A K，VANDEWALLE J.Least squares support vector machine classifiers[J].Neural Processing Letters，1999，9（3）：293-300.

[19]SU Z Q，TANG B P，LIU Z R，et al.Multi-fault diagnosis for rotating machinery based on orthogonal supervised linear local tangent space alignment and least square support vector machine[J].Neurocomputing，2015，157（1）：208-222.

[20]李鑫滨，陈云强，张淑青.基于LS-SVM多分类器融合决策的混合故障诊断方法[J].振动与冲击，2013，19（32）：159-164.

（编辑：商丹丹）

Study on hunting instability of high-speed train based on EEMD and energy entropy

LIU Qi，NING Jing，YE Yunguang，CHEN Chunjun
（School of Mechanical Engineering，Southwest Jiaotong University，Chengdu 610031，China）

To address the issue of hunting instability for high-speed train，a new method which combines ensemble empirical mode decomposition（EEMD），entropy features and least squares support vector machine（LSSVM）was presented in this paper to diagnose hunting abnormal motion state of high-speed train.Firstly，the vibration signal was decomposed by EEMD.Then，sample entropy features，Shannon entropy features and energy entropy features of IMFs were extracted. Lastly，the features were trained and recognized by LSSVM respectively.The test results show that the method of EEMD entropy features-LSSVM can accurately recognize the instability state of hunting motion when the speed of train is up to 330-350km/h.Furthermore，what can be learned from the experiment is that as an input feature，the energy entropy recognition effect will be superior to Shannon entropy and sample entropy，up to 95%.

hunting instability；EEMD；IMF；entropy features；LSSVM

A

1674-5124（2017）05-0096-05

10.11857/j.issn.1674-5124.2017.05.020

2016-08-20；

2016-11-05

国家自然科学基金项目（51475387）

刘棋（1990-），男，四川自贡市人，硕士研究生，专业方向为智能化状态监测及故障诊断。