花岗岩风化土物理特征曲线间的相关性研究*
2017-06-07夏金文魏玉杰蔡崇法
夏金文 魏玉杰 蔡崇法
(华中农业大学资源与环境学院,武汉 430070)
花岗岩风化土物理特征曲线间的相关性研究*
夏金文 魏玉杰 蔡崇法†
(华中农业大学资源与环境学院,武汉 430070)
花岗岩风化壳水分及收缩特性的研究是花岗岩土体稳定性评价及侵蚀机理研究的基础。通过Van Genuchten(VG)模型对不同风化程度的花岗岩土壤的颗粒累积分布、土水特征曲线和收缩特征曲线进行拟合,分析曲线拟合参数间以及这些参数与基本物理性质间的线性及非线性相关关系。结果表明:VG模型可以很好地用于不同风化程度花岗岩风化土的颗粒组成、土水特征与收缩特征的拟合与预测;曲线拟合参数间具有一定的线性相关关系;曲线拟合参数与基本物理性质间具有一定的线性相关关系,其中土水特征曲线参数与土壤质地以及容重线性相关性较高,收缩特征曲线物理参数与基本物理性质间的线性相关性较收缩特征曲线其他参数高。此外,曲线拟合参数间以及这些参数与基本物理性质间具有一定的非线性相关关系,而关系多为二次、三次非线性相关。根据花岗岩风化土颗粒组成状况及其基本物理性质对其水分特征曲线及收缩特征曲线进行预测具有一定的可行性。
花岗岩;颗粒分布;土水特征曲线;收缩特征曲线;Van Genuchten模型
水分特征作为分析与研究非饱和土力学问题的基础和重要部分[1],被广泛用于非饱和土稳定性评价,土壤水分变化引起的体积收缩对土体稳定性也具有重要影响[2-3],土水特征、收缩特征曲线在非饱和土稳定性研究方面具有重要作用。但目前有关土壤水分与收缩特性的测定方法多耗时费力,对设备要求较高。并且有关土壤收缩特性的研究大多集中在测量方法的改进和曲线拟合方面[4-5],鲜有研究探讨有关土壤收缩曲线间接推求的方法。此外,在土壤水分特征研究方面,近年来有学者通过多重回归[6]及物理经验模型[7]对水分特征进行预测,而这些方法大都适用于单个含水量点下的水分特征参数的预测,很难得到连续的水分特征曲线[8]。基于结构性土壤颗粒累积分布曲线、水分特征曲线形状上的相似性,有研究通过颗粒组成对水分特征曲线进行连续预测[9],但多数模型对细粒土的水分特征曲线预测效果相对较差,拟合预测效果也因不同土壤类型及模型而存在差异。
目前,针对花岗岩风化土的研究多集中于其成土过程和侵蚀环境因素方面[10],而关于其粒度组成及物理力学特性的研究鲜有报道。花岗岩风化壳从上到下风化程度的差异,导致其颗粒组成具有较大的空间异质性。颗粒组成作为土壤的基本性质之一,对土壤的理化性质及过程影响较大[11]。此外,颗粒组成的测定方法相对简单成熟,通过研究土壤颗粒累积分布曲线与水分、收缩特征曲线之间的联系,对预测土壤水分特征及收缩特性具有十分重要的意义。在这一方面,通过土壤颗粒分布曲线预测水分特征曲线的研究已有很多且较为深入,但关于土壤颗粒分布曲线与收缩特征曲线联系的研究则甚少。Braudeau等[12]通过XP模型对雏形土的收缩特征曲线和水分特征曲线进行拟合,发现这两种特征曲线均在同一质量含水率下发生转折,同时研究了土水特征、收缩特征曲线间的相似性,而颗粒累积分布曲线及土水特征曲线间的相似性也被广泛研究[7,9,13],这为收缩特征曲线的预测提供了一种新的思路和方法。因此,本文通过van Genuchten模型对花岗岩风化壳不同层次土壤的颗粒累积分布、水分特征曲线及收缩特征曲线进行拟合,分析颗粒组成与其他两种特征曲线参数间以及曲线拟合参数与基本物理性质间的线性相关关系,并通过回归分析建立拟合参数间及其与基本物理性质间的非线性回归方程,以期充分认识花岗岩土壤物理特征曲线间的关系,达到预测土水特征、收缩特征曲线的目的,为花岗岩地区的土壤侵蚀研究奠定基础。
1 材料与方法
1.1 研究区概况与实验方法
研究区位于湖北省东南部咸宁市通城县,湘、赣、鄂三省交界处,县域内崩岗数量达1 100多处,占湖北省崩岗总数的47%,是崩岗集中分布的典型区域。全县平均气温16.7 ℃,多年平均降雨量1 513 mm,多年平均径流深795 mm。该地区花岗岩出露面积占地区总面积的70%,水土流失总面积为38 410 hm2,在通城地区开展崩岗研究工作具有很强的代表性。
经过野外调查,在通城县五里镇五里社区(113°46′26″ E,29°12′39″ N)的典型崩岗发生区进行采样。根据花岗岩的风化程度将采样剖面划分为淋溶层(0~30 cm)、淀积层(30~65 cm)、过渡层1(65~120 cm)、过渡层2(120~200 cm)、母质层(>200 cm)的土壤进行试验(编号分别为L1、L2、L3、L4和L5)。分别用离心机配套环刀(20 cm2×5 cm)和收缩仪配套环刀(30 cm2×2 cm)在各层次取原状土,采样后迅速将环刀试件放入塑封袋内密封包装,并采集散状土样放入取样袋内,风干后按物理性质分析方法的要求过筛备用。
1.2 测定方法
土壤基本物理性质按常规测定方法测定[14]:饱和导水率采用TST-55型土壤渗透仪测定;土壤比重采用比重瓶法测定;容重采用环刀法测定;机械组成采用筛分法结合吸管法测定;土壤质地采用美国制的土壤质地分类标准进行确定;土水特征曲线采用离心法测定,离心过程中土壤体积的变化采用游标卡尺测量;收缩特征曲线采用SS-1型土壤收缩仪测定;土壤颗粒累积粒径分布特征曲线采用激光粒度仪测定。实验土壤的基本物理性质指标见表1。
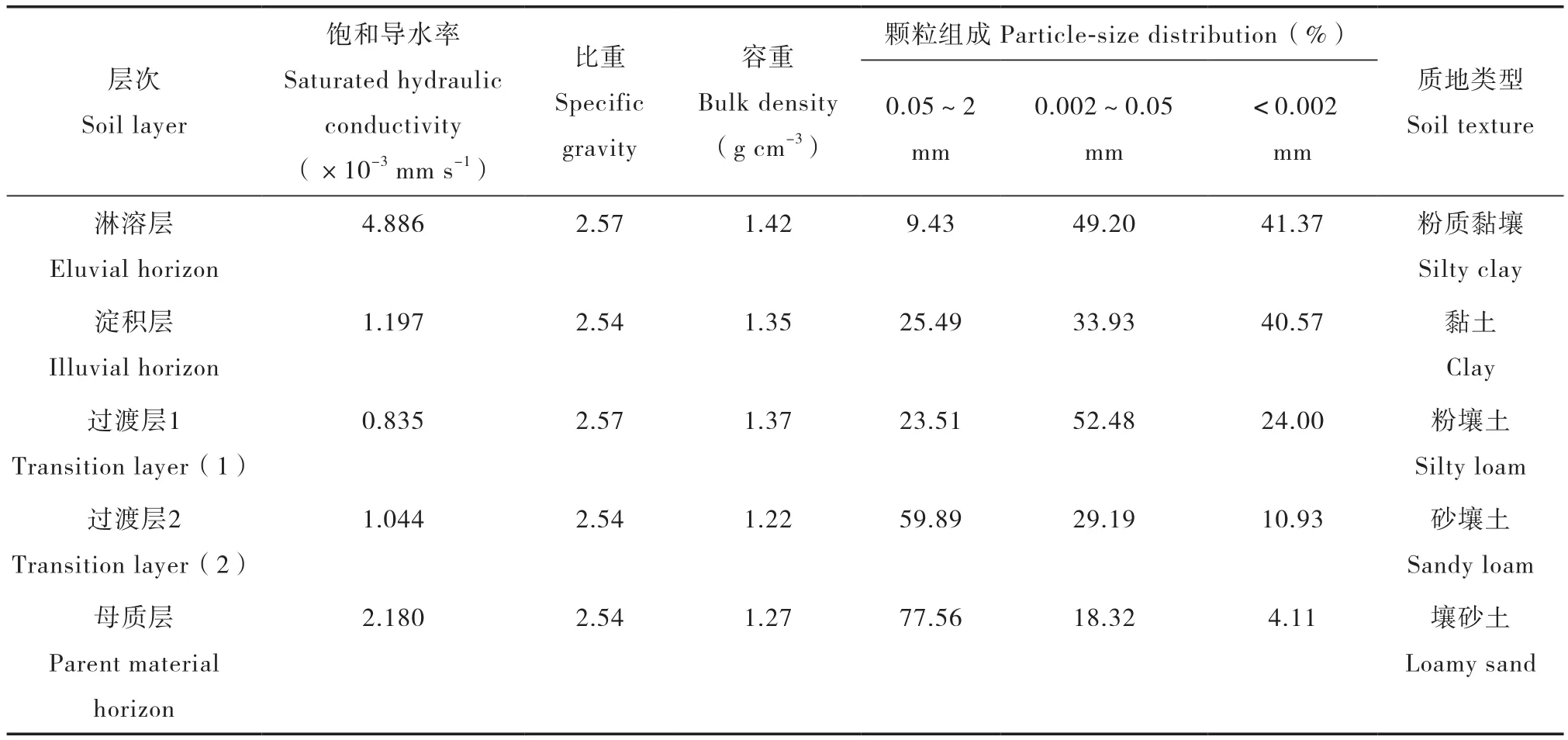
表1 供试土壤基本物理性质指标Table 1 Physical properties of tested soil
1.3 研究方法
对于模型的选用,能拟合土水、收缩特征曲线以及颗粒累积分布曲线的模型有很多[8-9,12],其中Van Genuchten模型(文中简称VG模型)是一种物理经验模型,能很好地拟合多种质地土壤,因此该模型被广泛应用于拟合土水、收缩特征曲线以及颗粒累积分布曲线等多种S型曲线,拟合效果良好[15-19]。
VG模型最初用于描述土壤水分特征曲线,其表达式为[19]:
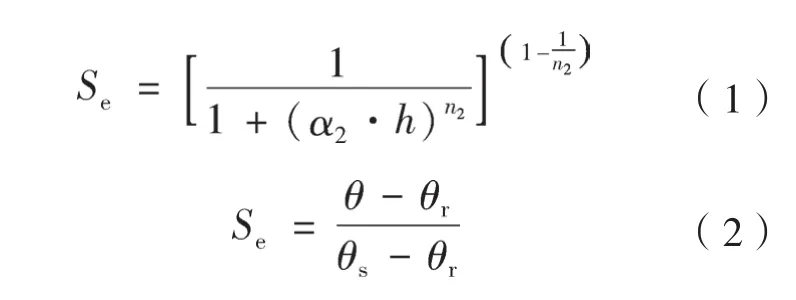
式中,Se为有效饱和度;θ代表土壤体积含水量(cm3cm-3);h为压力水头(cm);θr和θS分别代表土壤的残余体积含水量和饱和体积含水量(cm3cm-3);α2(cm-1)和n2为经验拟合参数(或曲线性状参数)。
土壤水分特征曲线为S型曲线,而收缩特征曲线以及颗粒分布曲线则为相反的倒S型曲线。水分特征曲线中参数n控制曲线斜率,因此,用-n来代替式(1)中的n,用c(小于某粒径的质量百分含量)和D(颗粒粒径)分别代替θ和h,经转化,得到如下的颗粒累积分布公式[16]:
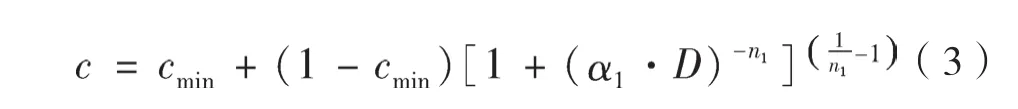
式中,α1、n1为曲线的形状参数;c为小于某粒径的质量百分含量(%);D为颗粒粒径(μm);Cmin为对应于最小粒径Dmin的累积百分含量,本文假设为0。
用-n来代替式(1)中的n,v(土壤比容积)和w(土壤质量含水量)分别代替θ和h,经转化,得到如下的收缩特征曲线公式[17]:
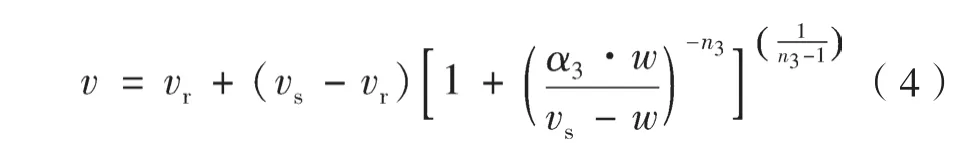
式中,v为土壤比容积(cm3g-1);w为土壤质量含水量(g g-1);vs和vr分别代表土样最大和最小的比容积(cm3g-1);α3(cm-1)和n3为经验拟合参数(或曲线性状参数)。
1.4 数据处理
水分特征曲线采用RETC软件求解,模型拟合采用Origin Pro8.0,参数间相关分析采用SPSS18.0 的Pearson相关系数法,非线性相关性分析采用SPSS18.0的非线性回归分析。
2 结果与讨论
2.1 Van Genuchten模型拟合颗粒分布曲线
土壤颗粒累积分布曲线与式(3)拟合曲线分别如图1中虚线与实线所示。从图中可以看出,供试土壤的颗粒累积分布曲线总体上呈S形,土壤颗粒直径在1~10 μm和100~1 000 μm范围内曲线平滑,在10~100 μm范围内曲线较陡,说明土壤颗粒累积含量主要分布范围10~100 μm;此外,中粒径范围内,实测值与拟合值总体上吻合度较高,而大粒径(>100 μm)和小粒径(<2 μm)范围内,实测值与拟合值均呈现一定程度的差异,表明VG模型对土壤大颗粒以及较小颗粒的累积分布曲线拟合效果稍差。
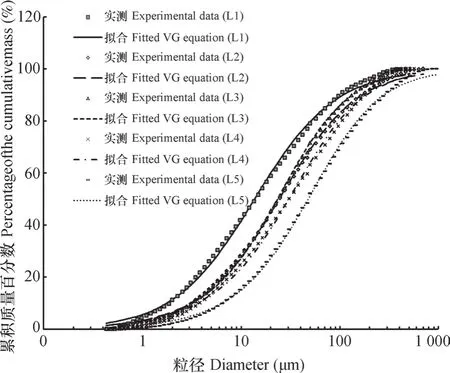
图1 Van Genuchten模型拟合的颗粒累积百分含量曲线Fig. 1 Cumulative fraction content fitted by VG model in percentage
式(3)拟合崩岗不同质地土壤颗粒的累积分布曲线在p<0.01下均达到显著水平,且具有较高的决定系数(R2>0.99)和较低的RMSE值(<3.00),表明VG模型可以很好地模拟花岗岩风化土的颗粒分布情况,并且其拟合参数能够很好地预测土壤颗粒组成状况[12]。表2表示土壤颗粒累积分布曲线VG模型拟合参数与基本物理性质间的线性相关关系。从表2可以看出,土壤颗粒累积分布曲线VG模型拟合参数α1与基本物理性质间的线性相关性较高,其中参数α1与砂粒呈显著的负相关关系(p<0.01,r=-0.919),而参数n1与基本物理性质间的线性相关性较差。

表2 土壤颗粒累积分布曲线VG模型拟合参数与基本物理性质间的相关关系Table 2 Correlation coefficient between VG model fitted parameters of cumulative fraction distribution curve and soil physical properties
2.2 Van Genuchten模型拟合土水特征曲线
VG模型拟合不同质地土壤的水分特征曲线如图2所示。由图2可知,随着基质吸力的增大,土壤体积含水量逐渐减小,但不同质地的土壤在不同的吸力阶段减小的快慢不同;当h<20 cm时,砂粒含量相对较高的L4和L5(砂壤土与壤砂土)体积含水量θ最高,但随基质吸力的增加降低较快,而黏粒含量相对较高的L1与L2(粉质黏壤土与黏土)最小,含水量随吸力变化较小;当h>20 cm时,随着基质吸力的增加,各层土壤含水量降低速率增加,其中砂粒含量较高的土壤(L4与L5)体积含水量θ急剧减小,且在所有供试土样中,其含水量最低,而粉粒含量最高的L3土样体积含水量减小仍然相对较慢,含水量最高;随着基质吸力进一步增大,当h达到一定值时,土壤体积含水量随基质吸力变化又趋于平缓,如对于L4与L5而言,当h>104 cm时,体积含水量低于0.10 cm3cm-3,而对于L3(粉壤土),当h>105cm时,含水量变化趋于平稳;对于L1(粉质黏壤)和L2(黏土),h则需大于2×105cm;在高吸力阶段黏粒含量最高的L1土样持水量最高。

图2 Van Genuchten模型拟合的土水特征曲线Fig. 2 Soil water retention curves fitted by VG model
式(1)和式(2)拟合崩岗不同质地土壤颗粒的水分特征曲线在p<0.01下均达到显著水平,R2均大于0.99且RMSE小于1,表明VG模型可以很好用于不同风化程度的花岗岩母质土壤的水分特征曲线拟合。随着质地由砂变黏,参数θS、α2、n2总体上呈现逐渐减小的趋势。VG模型拟合土壤水分特征曲线的拟合参数与基本性质间的相关分析(表3)表明,土水特征曲线参数θS、α2、n2与土壤质地以及容重线性相关性最高,其次是比重和饱和导水率,其中参数θS与容重、砂粒分别呈极显著负相关(r=-0.974,p<0.01)与极显著正相关(r=0.963,p<0.01),与黏粒呈显著负相关(r=-0.933,p<0.05);参数α2与砂粒及粉粒呈显著正相关,相关系数分别为0.891和0.881;参数n2与容重、砂粒分别呈显著负相关(r=-0.939,p<0.05)与显著正相关(r=0.924,p<0.05),与黏粒呈极显著负相关(r=-0.968,p<0.01)。
颗粒累积分布曲线与水分特征曲线的VG模型参数线性相关性分析表明,颗粒累积分布曲线中的参数α1、与水分特征曲线模型中的参数θS、α2及n2的相关性较高,其中参数α1与θS的线性相关性在p<0.01下达到显著水平,呈现显著的线性相关关系(r=-0.884,p<0.05),而参数n1与水分特征曲线模型中的参数θS、α2及n2的线性相关性较差。
水分特征是分析非饱和土力学的基础和重要部分,对研究土壤水分渗透、运移等有重要意义。然而,直接测量水分特征曲线耗时费力,因此关于如何准确预测土水特征成为了研究热点。关于水分特征曲线的预测方法较多,其中一个很重要的研究点是运用土壤转换方程(PTFs)来预测土水特征曲线。运用土壤转换方程的前提是土水特征参数与基础物理性质间的高相关性,才能采用基础物理性质对土水特征参数进行转换。目前。关于水分特征曲线的预测运用得最多的基础物理性质有土壤颗粒分布、有机质、容重以及颗粒密度[13,18]等,预测所用数据库和土壤种类较多,但关于土水特征曲线的预测多为单点非连续预测,能得出连续的土水特征曲线较少。本文运用同一模型拟合土水特征及颗粒分布曲线,并对两曲线参数进行线性相关分析,得出参数间的高相关性,为土水特征的连续预测奠定了基础。

表3 水分特征曲线VG模型拟合参数与基本物理性质间的相关关系Table 3 Correlation coefficient of VG model fitted parameters of soil water retention curve and soil physical properties
2.3 Van Genuchten模型拟合收缩特征曲线

图3 Van Genuchten模型拟合的收缩特征曲线Fig. 3 Soil contraction characteristic curve fitted by VG model
VG模型拟合不同质地土壤的收缩特征曲线如图3所示。由图可知,随着含水率的降低,土壤比容积逐渐减小并最终趋于稳定;除L5外,其余各土样比容积随着含水率减小而减小的速率先增大后减小,其中L1土样在含水率约为17%时土样体积随含水率的变化最剧烈,L2与L3土样均在含水率约20%时土壤体积对水分变化最敏感,L4土样在含水率约为25%时最敏感;由于供试土样从自然含水率开始脱水收缩,因此所有试验均不存在明显的结构收缩阶段,其中L2和L3土样的收缩曲线则可以明显的区分为正常收缩、残余收缩与零收缩三个阶段[20];此外,L2土样在含水率为15%~30%时,土壤比容积变化最剧烈,其次为L1土样,而L4与L5土样总体上较容积对水分的变化不敏感,表明质地由黏到砂土壤体积随含水率的变化逐渐不明显;随着含水率的降低,L1、L2和L3三个供试土样在含水率降低至25%左右时土壤比容积不再产生明显变化,而L4土样则在10%时土壤比容积趋于稳定。
式(4)拟合崩岗不同质地土壤颗粒的收缩特征曲线在p<0.01下均达到显著水平,且R2均大于0.99而且RSME很小,说明VG模型可以很好地用于不同风化程度花岗岩土样收缩特征曲线的拟合。VG模型参数与基本物理性质间的相关分析(表4)表明,收缩特征曲线VG模型拟合参数vr、vs与基本物理性质间的线性相关性较高,其中参数vr与容重呈显著负相关关系(r=-0.898,p<0.05),与砂粒含量呈显著正相关关系(r=0.905,p<0.05),参数vs与比重呈显著负相关关系(r=-0.928,p<0.05),其次是参数n3与α3。总体而言,收缩特征曲线参数受土壤质地影响较大,其次是容重、饱和导水率以及比重。
颗粒累积分布曲线与收缩特征曲线的VG模型参数线性相关分析表明,颗粒累积分布曲线模型的参数α1与收缩特征曲线模型中的参数vr、vs的相关性相对较高,其中参数α1与收缩特征参数vr呈极显著负相关关系(r=-0.990,p<0.01),而参数n1与收缩特征曲线模型中参数的线性相关性较差。
土壤的收缩特征是指土体随着自身含水率降低而产生体积减小的现象,土壤在干旱收缩过程中会引起土体的收缩变形,降低土体强度、承载力和稳定性[21],破坏土壤中作物的根系,促进土壤水分的蒸发,改变地表水的径流及土壤水分、养分和微生物的迁移规律等[22],因此在农业和工程中,对土壤收缩特征的研究均极其重要。目前关于收缩特征曲线的研究,大多集中在收缩曲线模型的拟合与改进以及土壤收缩过程及收缩特征研究方面,而关于收缩特征曲线与土壤其他特征曲线间的关系及其间接推求方法则研究较少。本文通过研究收缩特征曲线与颗粒分布曲线间参数以及基础物理性质间的关系,对探求土壤收缩特征曲线的间接推求方法有重要意义。
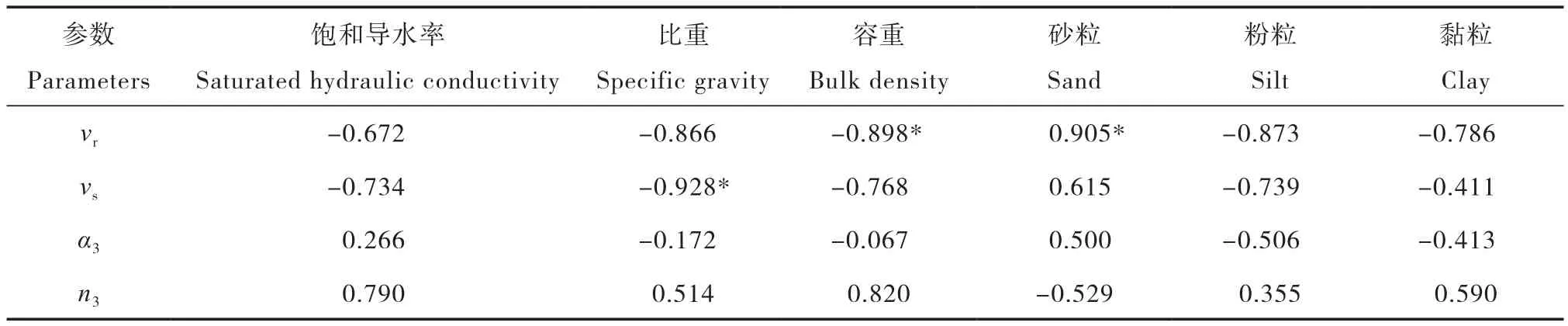
表4 收缩特征曲线VG模型拟合参数与基本物理性质间的相关关系Table 4 Correlation coefficient of VG model fitted parameters of soil contraction characteristic curve and soil physical properties
2.4 Van Genuchten模型拟合曲线参数间回归方程
前面讨论了各拟合曲线参数间以及这些参数与基本物理性质间的线性相关关系,可以看出,部分参数间及其与基本物理性质间具有一定的线性相关性。理论上,收缩特征和土水特征参数均受到颗粒累积分布曲线参数的影响,并且这三种曲线参数均与基本物理性质有关。有研究表明,黏粒含量对土壤收缩特征及土水特征影响显著[23-24],砂粒对土体收缩起抑制作用[4,25],颗粒累积分布也多被用于预测土水特征曲线,这些研究均说明这三种曲线参数间及其与物理性质间具有一定的相关关系,但这些研究多用线性相关关系来说明和讨论特征参数与基本物理性质间的关系,而关于它们间的非线性回归方程的建立则较少。
为进一步分析各拟合曲线参数间以及这些参数与基本物理性质间的相关关系,通过统计回归分析,分析部分参数间及其与基本物理性质间的非线性相关性,分析结果如表5。表5中的方程均通过了显著性检验(p<0.05),未通过显著性检验的方程未标注于表中。从表5中可以看出,水分特征曲线参数α2与黏粒以及颗粒分布曲线参数α1具显著的二次非线性相关关系,决定系数达到0.998和0.964;收缩特征曲线参数α3与砂粒具显著的三次非线性相关关系,决定系数达到0.998;收缩特征曲线参数vs与颗粒分布曲线参数n1具显著的三次非线性相关关系。

表5 曲线参数与物理性质间的非线性回归方程Table 5 Nonlinear regression equations
3 结 论
根据花岗岩风化土颗粒累积分布、水分特征、收缩特征曲线间的相似性以及三种曲线间及其与基本物理性质间的内在联系,通过VG模型对不同风化程度的花岗岩土壤的颗粒累积分布、土水特征曲线和收缩特征曲线进行拟合,分析曲线拟合参数间以及这些参数与基本物理性质间的线性及非线性相关关系。结果表明,VG模型可以很好地用于不同风化程度花岗岩风化土的颗粒组成、土水特征与收缩特征的拟合与预测;曲线拟合参数间具有一定的线性相关关系,其中颗粒累积分布曲线参数α1分别与土水特征曲线参数θS以及收缩特征参数vr呈显著的线性相关关系(r=-0.884,p<0.05)和极显著负相关关系(r=-0.990,p<0.01);曲线拟合参数与基本物理性质间具有一定的线性相关关系,其中土水特征曲线参数θS、α2、n2与土壤质地以及容重线性相关性较高,收缩特征曲线参数vr、vs与基本物理性质间的线性相关性较收缩特征曲线其他参数高;曲线拟合参数间以及这些参数与基本物理性质间具有一定的非线性相关关系,其中水分特征曲线参数α2与黏粒以及颗粒分布曲线参数α1均具显著的二次非线性相关关系,收缩特征曲线参数α3与砂粒以及收缩特征曲线参数vs与颗粒分布曲线参数n1均具显著的三次非线性相关关系。本研究为花岗岩风化土物理特征曲线间相互关系的研究奠定了基础,说明根据花岗岩风化土颗粒组成状况及基础物理性质对其水分特征曲线及收缩特征曲线进行预测具有一定的可行性。
[1] Fredlund D G,Rahardjo H. Soil mechanics for unsaturated soils. New York:Wiley,1993
[2] Lan H X,Hu R L,Yue Z Q,et al. Engineering and geological characteristics of granite weathering profiles in South China. Journal of Asian Earth Sciences,2003,21(4):353—364
[3] Fredlund D G,Morgenstern N R,Widger R A. The shear strength of unsaturated soils. Canadian Geotechnical Journal,1978,15(3):313—321
[4] 刘平,张虎元,严耿升,等. 土建筑遗址表部土体收缩特征曲线测定. 岩石力学与工程学报,2010,29 (4):842—849
Liu P,Zhang H Y,Yan G S,et al. Determination of soil shrinkage characteristic curve of surface soil on ancient earthen architectures(in Chinese). Chinese Journal of Rock Mechanics and Engineering,2010,29 (4):842—849
[5] 栾茂田,汪东林,杨庆,等. 非饱和重塑土的干燥收缩试验研究. 岩土工程学报,2008,30(1):118—122
Luan M T,Wang D L,Yang Q,et al. Experimental study on drying shrinkage of unsaturated compacted soils(In Chinese). Chinese Journal of Geotechnical Engineering,2008,30(1):118—122
[6] Nielsen D R. Development of pedotransfer functions in soil hydrology. Geoderma,2006,136:470—472
[7] Haverkamp R,Leij F J,Fuentes C,et al. Soil Water Retention :I. Introduction of a Shape Index. Soil Science Society of America Journal,2005,69(69):95—104
[8] Mohammadi M H,Meskini-Vishkaee F. Predicting Soil Moisture Characteristic Curves from Continuous Particle-Size Distribution Data. Pedosphere,2013,23 (1):70—80
[9] Sang I H,Powers S E. Using particle-size distribution models to estimate soil hydraulic properties. Soil Science Society of America Journal,2003,67(4):1103—1112
[10] Mareschal L,Turpault M P,Ranger J. Effect of granite crystal grain size on soil properties and pedogenic processes along a lithosequence. Geoderma,2015,249:12—20
[11] Rahardjo H,Indrawan I G B,Leong E C,et al. Effects of coarse-grained material on hydraulic properties and shear strength of top soil. Engineering Geology,2008,101:165—173
[12] Braudeau E,Costantini J M,Bellier G,et al. New device and method for soil shrinkage curve measurement and characterization. Soil Science Society of America Journal,1999,63(3):525—535
[13] Arya L M,Paris J F. A physic-empirical model to predict the soil moisture characteristic from particlesize distribution and bulk density. Soil Science Society of America Journal,1981,45(6):1023—1030
[14] 依艳丽. 土壤物理研究法. 北京:北京大学出版社,2009
Yi Y L. Research methods for soil physics(in Chinese). Beijing:Peking University Press,2009
[15] 王小华,贾克力,刘景辉,等. Van Genuchten模型在土壤水分特征曲线拟合分析中的应用. 干旱地区农业研究,2009,27(2):179—183
Wang X H,Jia K L,Liu J H,et al. Application of Van Genuchten model to analysis of soil moisture characteristic curve(in Chinese). Agricultural Research in the Arid Areas,2009,27(2):179—183
[16] Zhuang J,Yan J,Miyazaki T. Estimating water retention characteristic from soil particle-size distribution using a non-similar media concept. Soil Science,2001,166:308—321
[17] Peng X,Horn R. Modeling soil shrinkage curve across a wide range of soil types. Soil Science Society of America Journal,2005,69(3):584—592
[18] Van Genuchten M T. A closed-form equation forpredicting the hydraulic conductivity of unsaturated soils. Soil Science Society of America Journal,1980,44(5):892-898
[19] 邓羽松,丁树文,蔡崇法,等. 鄂东南崩岗剖面土壤水分特征曲线及模拟. 土壤学报,2016,53(2):355—364
Deng Y S,Ding S W,Cai C F,et al. Characteristic Curves and Model Analysis of Soil Moisture in Collapse Mound Profiles in Southeast Hubei(in Chinese). Acta Pedologica Sinica,2016,53(2):355—364
[20] 邵明安,吕殿青. 土壤收缩特征曲线的实验研究. 土壤学报,2003,40(3):471—474
Shao M A,Lü D Q. Experimental study on soil shrinkage characteristic curves(in Chinese). Acta Pedologica Sinica,2003,40(3):471-474
[21] Rayhani M H T,Yanful E K,Fakher A. Desiccationinduced cracking and its effect on the hydraulic conductivity of clayey soils from Iran. Canadian Geotechnical Journal,2007,44(3):276—283
[22] Bronswijk J J B,Hamminga W,Oostindie K. Fieldscale solute transport in a heavy clay soil. Water Resources Research,1995,31(3):517—526
[23] 魏玉杰,吴新亮,蔡崇法. 崩岗体剖面土壤收缩特性的空间变异性. 农业机械学报,2015,46(6):153—159
Wei Y J,Wu X L,Cai C F. Spatial Variability of Soil Shrinkage Characteristics in Profile of Slope Disintegration Body(in Chinese). Transactions of the Chinese Society of Agricultural Machinery,2015,46 (6):153—159
[24] 林琳,韩少杰,王恩姮. 有机质与黏粒含量对黑土压缩-回弹特性的影响. 土壤学报,2016,53(5):1138—1147
Lin L,Han S J,Wang E H. Effect of organic matter and clay content on compression-rebound characteristics of black soil(in Chinese). Acta Pedologica Sinica,2016,53(5):1138—1147
[25] Indrawan I G B,Rahardjo H,Leong E C. Effects of coarse-grained materials on properties of residual soil. Engineering Geology,2006,82(3):154—164
Correlations between Characteristic Curves of Physical Properties of Weathered Granite Soils
XIA Jinwen WEI Yujie CAI Chongfa†
(College of Resource and Environment,Huazhong Agricultural University,Wuhan 430070,China)
【Objective】Researches on moisture content and contraction characteristics of weathering crust of granite are the basis for evaluation of stability of granite soil and studies on erosion mechanism of the soil. However,direct measurement of the two parameters is very tedious,time consuming,and errors prone. Therefore,a number of indirect measuring methods have been developed to predict soil water retention curves by means of determining particle-size distribution,but most of these methods often yield intermittent soil moisture characteristic data because they are only capable of predicting soil moisture characteristic at individuals points along the curves. It is,therefore,essential to explore for a new method to plot characteristic curves of soil water content and contraction of weathering crust of granite. For that end,it is a first priority to understand relationships between soil moisture retention curve,contraction characteristic curve and particle-size distribution curve,as well as relationships between all the three curves and physical properties of the soil.【Method】To comprehensively understand the relationships,soil samples different in weathering degree were collected from Southeast Hubei for analysis. Based on the similarity of the soil water retention curves,contraction characteristic curves and particle-size distribution curves,the Van Genuchten(VG)model was used to fit the curves of the soil samples different in weathering degree and explore fitting parameters of the curves and linear and non-linear correlations of the fitting parameters with soil physical properties.【Result】Results show that,the VG model may well fit all the three curves of granite soils different in weathering degree. Certain linear relationships were found between the fittingparameters,particularly between parameter α1of the particle-size distribution curves and parameter θSof soil water retention curves(r=-0.884,p<0.05)and but highly significant negative linear ones were between α1and parameter vrof the contraction characteristic curves(r=-0.990,p<0.01);Meanwhile,certain linear relationships were also found between the curve fitting parameters and basic soil physical properties,especially those of the parameters of water retention curves with soil texture and bulk density. And the linear relationships of parameters vrand vsof the contraction characteristic curves with basic soil properties were closer than those of all the others;Besides non-linear relationships also exsited between fitting parameters of these curves and between the parameters and basic soil physical properties. Significant quadratic nonlinear relationships were found of parameter α2of the water retention curves with the clay and parameter α1of the particle-size distribution curves,while significant cubic ones were between parameter α3of the contraction characteristic curves and sand,and between parameter vsof the contraction characteristic curves and parameter n1of the particle-size distribution curves.【Conclusion】In this paper,the VG model was used to fit paricle-size distribution,soil moisture content and contraction characteritics of granite soils different in weathering degree and analyze linear and non-linear relationships between soil water retention curves,contraction characteristic curves and particle-size distribution curves,between fitting parameters of the three types of curves and between the fitting parameters and basic physical properties of the soil. All the findings will certainly be useful to future study on relationships between the three types of curves and have demonstrated that it is feasible to predict soil moisture content and contraction characteristics of granite soils based on their particle-size distribution and physical properties.
Granite;Particle-size distribution;Soil water retention curve;Soil contraction characteristic curve;Van Genuchten model
S152.7
A
(责任编辑:檀满枝)
* 国家自然科学基金项目(41630858)资助 Supported by the National Natural Science Foundation of China(No. 41630858)
† 通讯作者 Corresponding author,E-mail:cfcai@mail.hzau.edu.cn
夏金文(1992—),男,湖北鄂州人,硕士研究生,主要从事崩岗边坡稳定性研究。E-mail:xjw.hzau.edu.cn@
webmail.hzau.edu.cn
2016-06-11;
2016-11-09 ; 优先数字出版日期(www.cnki.net):2017-01-03
10.11766/trxb201606110214
