基于约束HMM的变点检测算法①

庄 玉,何振峰

(福州大学 数学与计算机科学学院,福州 350108)

基于约束HMM的变点检测算法①

庄 玉,何振峰

(福州大学 数学与计算机科学学院,福州 350108)

时间序列的变点分析在现今社会各个领域中都有着广泛的应用.针对时间序列进行变点分析中要求变点状态需要连续持续一定的时间的应用背景,提出了一种结合状态最短连续长度约束的隐马尔可夫模型.给出了约束Baum-Welch训练算法和约束Viterbi状态提取算法.应用在仿真数据和GNP数据集的实验表明,结合状态最短连续长度约束的HMM相比于一般HMM在时间序列变点检测中效率较高.

变点检测;约束隐马尔可夫模型;时间序列分割

时间序列是随时间次序而变化的一系列数据,是一类多维的复杂类型数据[1].当所观察的时间序列跨越时间越长时,形成的时间序列的随机变量会由于某种条件的变化,从某时间点开始不再服从原来的分布,即出现了变点.随着变点问题应用的愈加广泛,在一些文献中有许多同义词,包括了结构断点[2],时间序列分割[3],和检测“异常点”[4].

时间序列的变点检测方法可以很好的用HMM来建模,其中时间序列数据就是HMM中的输出符号,可以通过时间序列数据来检测所处的状态,判断是否出现变点.一般的HMM对隐状态链没有任何限制,即在隐状态链中可以自由的从一个状态转移到其他任何一个状态.这样的HMM称为无约束HMM.在实际工作中,需要解决的问题一般有领域背景.希望训练出的HMM符合用户的预期.例如,在经济学中,至少要有两个连续的负增长(收缩)状态,才能说这段时间处于经济衰退期[5];在遗传学中,一个罕见的遗传现象比如,至少要有几百个碱基长,才能被认为出现了CpG island(Aston and Martin,2007)[6].

针对于此,本文提出了一种结合状态最短连续长度约束的隐马尔可夫模型,一般的HMM假设时间序列是由一系列隐状态构成,而系统的运行本质就是在不同的隐状态间转换,一般的HMM对隐状态之间转换没有限制,本文的方法限制了状态之间的转换.首先扩展状态数为原来的倍,并在训练模型时加约束,限制了状态之间转移,这样学习出约束HMM就自带限制最小变点连续长度,满足在一些特定的应用情况下要求状态持续的长度限制.在解码隐状态序列时,控制最后一个状态一定是扩展状态的最后一个,就能保证只要序列中出现状态变化即出现变点,并且状态已经持续至少h.并将该模型应用在两组已控制变点位置的模拟数据和GNP数据集,检测其变点.

1 相关工作

变点问题的研究始于Page在Biometrika上发表的一篇关于连续抽样检验的文章[7].近二十年来,变点问题的研究在理论和世纪应用等方面有了快速的发展.理论上已有了一系列较为成熟的结果,国外的变点的应用研究主要涉及金融股票市场检测[8]、环境检测[9]、医药与生物工程[10]、系统维护[11]等.我国学者对变点问题的研究始于上世纪80年代,由陈希孺教授和缪柏其教授利用“局部法”开始了变点的研究[12]．在我国对于变点问题的应用还是很少的,只在少数领域中获得了应用,如张学新等[13]研究了最小二乘法检测多个变点的性能,并成功检测出1952-2003年中国主要经济部门GNP的变点.

对实际应用背景下,Chib[14]和 Luong[15]提出了一种带约束的HMM即隐状态链中的状态转移是有一定限制的.Nam[16]提出了基于HMM的限制最小连续长度变点的定义,描述了一个基于该定义的约束HMM,但是他没有给出明确的约束模型的定义,没有说明状态迁移矩阵以及训练该模型的算法.他是用一般的训练算法来学习HMM,对于限制的最小变点连续长度是在分析隐序列时来约束,而且Nam提出的模型是用来做变点的风险分析.而本文提出的结合状态最短连续长度的约束HMM,描述其状态之间的迁移限制,给出了约束HMM的训练算法以及状态提取算法,用来解决实际问题中对于最小状态连续长度的限制的问题.

2 结合状态最短连续长度约束的HMM

2.1 隐马尔可夫模型

HMM是一种双重随机过程,一个是隐含的有限状态马尔可夫链即xt,它描述状态的转移,另一个描述状态与观察值之间的统计对应关系.在实际问题中我们只能看到观察值,而不能直接看到隐状态.只能通过研究观察值序列yt去推断隐状态序列xt[17].隐马尔可夫模型为一五元组其中:

状态转移概率矩阵:

A=(aij)N´N其中即由状态si转移到状态sj的概率且

2.2 变点

使用HMM为时间序列建模,在已知隐状态序列的情况下,时间序列变点的一般定义如定义1.

定义1.在t时刻隐状态链的状态改变,即t时刻出现变点,即:

然而,对于一些实际的应用中,确定一个变点,要求这个状态变化要持续一定的时间,比如第四部分的分析GNP数据的经济周期等,而用一般的HMM分析时,无法限制.在这些应用情况下,Nam定义一个持续的变点如定义2.

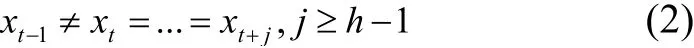
定义2的两个重要的特性:第一,与其他基于HMM 的变点方法相似,变点的分析是从隐状态序列推断的;第二,相比于分析隐马尔科夫链的状态变化,更重要的是分析在隐马尔科夫链中最短持续长度h的状态变化.第二个点就是本文提出结合最短连续长度约束HMM的主要思想.

2.3 结合状态最短连续长度约束的HMM确定在时间t出现变点,即:

针对Nam定义的持续的变点,本文提出结合状态最短连续长度约束的HMM,通过控制了状态之间的转移,来控制状态的最短连续长度,一个约束HMM为一新的五元组

与一般HMM不同的是,约束HMM在学习状态转移矩阵时,对状态之间的转移加上了限制.如图1为状态数为2,h=2时的状态转移图.初始状态只能从扩展状态的第一个状态开始,如图中的s11,s21,当处于同一个状态时,s11只能转移到s12,而处于s12时,说明s1这个状态已经持续了h=2,s12可达的状态可以是自身s12另一个状态的第一个扩展状态s21.在这样的限制下,就可以保证一个状态可以持续至少h=2.

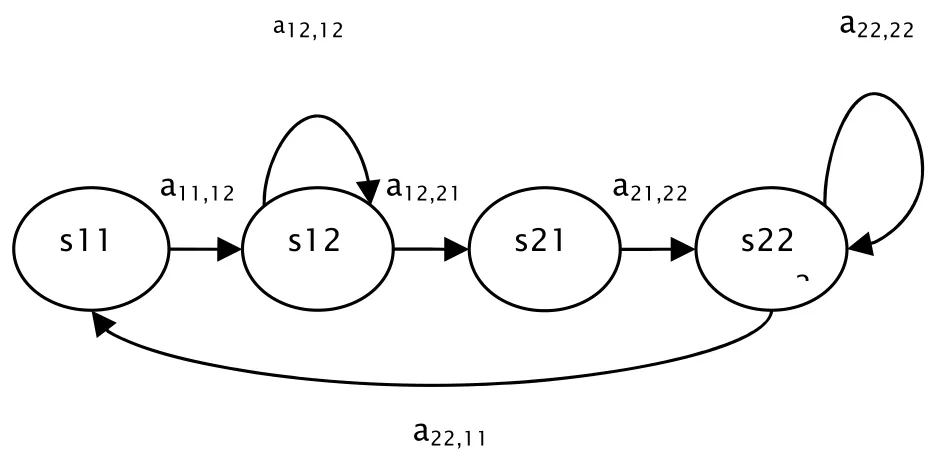
图 1 2-状态,h=2状态转移图

当h=1时,约束HMM就是一般HMM模型.

2.4 约束HMM的学习算法

Baum-Welch算法是隐马尔科夫模型学习问题的一种常用解决方法.约束HMM的学习算法是在Baum-Welch算法基础上加入状态最短连续长度的约束.训练约束HMM的过程如下:

2)计算辅助变量:

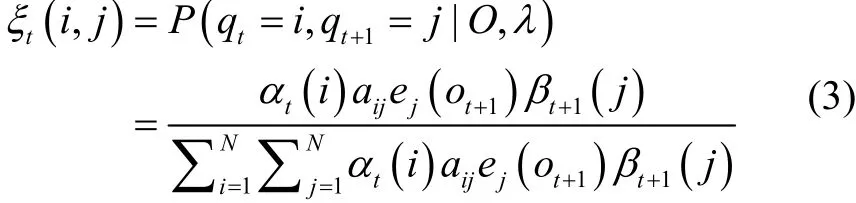
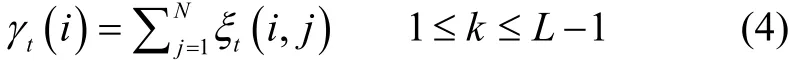
3)参数更新,重估公式:

与一般HMM不同,由于隐状态扩展为原来的h倍,初始状态只能从开始,即m¹1时,.

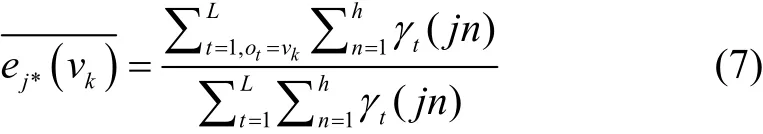
在每次循环的参数重估结束后,都要修改转移矩阵 A:当i=j时,当如果其他情况下当时,当m=1,n=h或者时,其他情况下控制状态之间的转移.

本文的方法与一般的Baum-Welch算法不同的地方就在于在参数重估步骤中,对初始概率,输出矩阵和状态转移矩阵的修改.

2.5 约束HMM的状态提取算法

解决给定模型及观测序列O,求生成此观测序列的最大可能的隐状态序列,一般采用的是Viterbi算法,解码最大可能的隐状态序列.

在分析隐状态序列变点时,有两种情况一种是隐状态序列最后一个状态允许是一半状态,另一种是状态必须满足h个,本文的方法是用到后一种情况来分析Viterbi序列.限制了隐状态序列最后一个状态一定是扩展状态的最后一个状态,保证了最后一个状态的持续时间也不小于h.算法1为约束HMM的状态提取算法.

与一般HMM不同的是,约束HMM要限制隐状态序列最后一个状态一定是扩展状态的最后一个状态,即一定是sih,本文状态提取算法与Viterbi算法不同之处是把其他扩展状态的设置为 -1.

3 实验

3.1 实验设计与数据准备

为了验证本文提出的约束HMM比一般的HMM在检测实际应用上的便捷性,我们将约束HMM应用到实际数据的处理与分析工作之中.

实验中用到的数据集:

①已控制变点位置的模拟数据,变点出现在t=10, t=20处.

第一组序列:

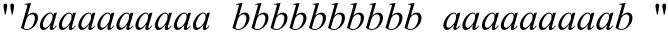
第二组序列:

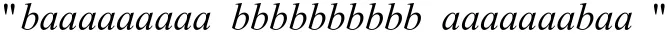
根据经济周期理论,一个完整的经济周期应包括复苏、高涨、衰退、萧条等四个阶段,故将GNP数据即观测序列离散化为四个观测值,离散化的结果如图2.

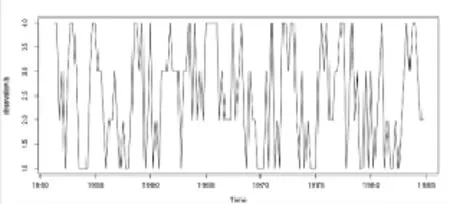
图 2 离散化后的GNP数据

基于约束HMM的变点检测方法步骤:

① 数据集,整理数据

②初始化约束HMM

③ 用约束Baum-Welch算法训练约束HMM

④ 用约束Viterbi算法解码隐状态序列

⑤ 根据实际应用背景分析隐状态序列变点

3.2 实验结果及分析

3.2.1 分别用约束HMM和HMM分析模拟数据

第一组序列:

用HMM为观察序列建模,得出隐状态链得到的是:

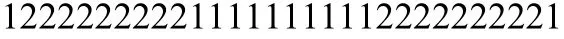
设定h=3,约束HMM得到的隐状态链为:

第二组序列:

用HMM得到隐状态链得到的是:

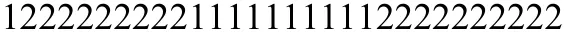
用约束HMM得到的隐状态链为:

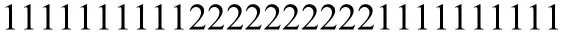
对比序列1和2的结果,一般HMM容易检测出小波动的变点,即状态改变只有一两个时间点,容易检测出额外的变点如t=1,t=29,而使用约束HMM就能够准确地检测到变点的位置,并保证了状态至少持续了h=3时间.

3.2.2 分别用约束HMM和HMM分析GNP数据的经济周期

根据离散化的GNP数据,观测值有四个为(“F”,“G”,“S”,“X”)分别代表一个完整经济周期的四个阶段:复苏、高涨、衰退和萧条.隐状态为(“K”,“S”)分别代表经济活动的扩张和收缩状态.在要求限定下,设置h=2.约束HMM隐状态扩展为(“K1”,“K2”,“S1”,“S2”).

用一般的HMM检测到的变点分布如图3所示.

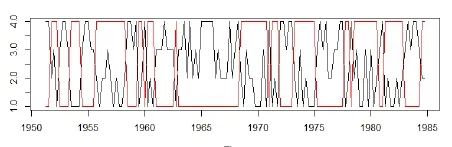
图 3 一般HMM检测到的变点分布

从图3可观察到检测出了12个变点,分别分布在1951/2～1952/2,1953/3～1954/2,1955/4～1958/2,1959/3～1 959/4,1960/2～1960/4,1962/4,1968/3～1970/4,1971/2～197 1/4,1973/2～1975/1,1977/4～1978/1,1978/3～1980/3,1981/ 2～1982/4,1984/3～1984/4

基于约束HMM检测到的变点如图4.

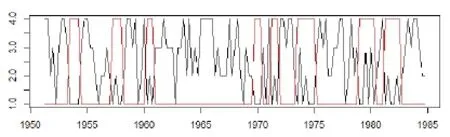
图 4 约束HMM检测到的变点分布

检测出 8个变点分别分布在 1953/2～1954/2, 1957/2～1958/1,1960/2～1960/1,1969/4～1970/2,1971/2～ 1971/4,1973/3～1975/1,1979/1～1980/2,1981/2～1982/3.

由一般HMM检测到的变点和约束HMM检测到的变点对比分析可得到,一般HMM检测到的变点,无法满足经济周期拐点的定义,即无法满足经济周期的衰退期至少持续两个季度,比如变点1962/4,该变点只有一个季度,无法判定为经济周期,并且变点与变点之间相距时间太短,如 1977/4～1978/1和1978/3～1980/3之间,约束HMM因为限制了h故不会出现这种情况.还可以观察到一般HMM会把数据开始和结束当做变点,这在约束HMM结果中不会出现.

4 结语

基于一般HMM的变点检测方法没有考虑到实际应用背景中要求变点状态持续一定时间,比如本文实验中检测经济周期时,需要衰退期至少持续两个季度.本文提出结合状态最短连续长度约束HMM通过控制状态之间的转移,能够有效的检测出时间序列的变点,并且满足相关应用背景对状态持续一定时间的要求.实验结果表明,较之一般HMM,约束HMM在保证检测变点准确度前提下,满足了状态最短持续时间,提高了变点检测效率.

1 Janacek G.Time series analysis forecasting and control. Journal of Time SeriesAnalysis,2010,31(4):303.

2 Davis RA,Lee TCM,Rodriguez-Yam G A.Structural break estimation for nonstationary time series models.Journal of theAmerican StatisticalAssociation,2006,101(473):223–239.

3 Cheong SA,Fornia RP,Lee GHT,et al.The Japanese economy in crises:A time series segmentation study. Economics:The Open-Access,Open-Assessment E-Journal, 2012,6(2012-5):1–81.

4 Zaccarelli N,Li BL,Petrosillo I,et al.Order and disorder in ecologicaltime-series:Introducing normalized spectral entropy.Ecological Indicators,2013,28(5):22–30.

5 Stock JH,Watson M W.Has the business cycle changed and why?Nber MacroeconomicsAnnual,2002,17(1):159–218.

6 Aston JAD,Martin DEK.Distributions associated with general runs and patterns in hidden Markov models.Annals ofApplied Statistics,2007,1(2):585–611.

7 Page ES.Continuous inspection schemes.Biometrika,1954, 41(1/2):100–115.

8 Tseng YH,Durbin P,Tzeng GH.Using a fuzzy piecewise regression analysis to predict the nonlinear time-series of turbulent flows with automatic change-point detection.Flow Turbulence&Combustion,2001,67(2):81–106.

9 Leonte D,Nott DJ,Dunsmuir WTM.Smoothing and change point detection for gamma ray count data.Mathematical Geology,2003,35(2):175–194.

10 Patra K,Dey DK.A general class of change point and change curve modeling for life time data.Annals of the Institute of Statistical Mathematics,2002,54(3):517–530.

11 Moltchanov D.State description of wireless channels using change-point statistical tests. Wired/wireless Internet Communications,2006,(3970):275–286.

12陈希孺.只有一个转变点的模型的假设检验和区间估计.中国科学,1988,31(8):817–827.

13张学新,段志霞.最小二乘法对多变点检验的性能研究.河南师范大学学报:自然科学版,2009,37(6):7–10.

14 Chib S.Estimation and comparison of multiple change-point models.Journal of Econometrics,1998,86(2):221–241.

15 Luong TM,Rozenholc Y,Nuel G.Fast estimation of posterior probabilities in change-point analysis through a constrained hidden Markov model.Computational Statistics &DataAnalysis,2013,(68):129–140.

16 Nam CFH,Aston JAD,Johansen AM.Quantifying the uncertainty in change points.Journal of Time Series Analysis,2012,33(5):807–823.

17 Concha OP,Xu RYD,Moghaddam Z,et al.HMM-MIO:An enhanced hidden Markov model for action recognition. CVPR Workshops,2011:62–69.

Change Point Detection Based on Constrained Hidden Markov Model

ZHUANG Yu,HE Zhen-Feng

(School of Mathematics and Computer Science,Fuzhou University,Fuzhou 350108,China)

The change point detection of time series is widely applied in various fields.In some applications,a minimum period is required before a state change.Motivated by such applications,a constrained Hidden Markov Model,which combines with the shortest state continuous length constraint,is proposed in this study.Moreover,a constrained Baum-Welch training algorithm and a constrained Viterbi state extraction algorithm are also given.And experimental results based on the simulation data and GNP data sets indicate that the constrained HMM has higher performance than the general HMM.

change point detection;constrained Hidden Markov Model;time series segmentation

2016-08-06;收到修改稿时间:2016-09-20

10.15888/j.cnki.csa.005712