基于深度优先搜索的正方化树图布局算法①

刘旭

(SAP中国研究院 商务智能部,上海 201203)

基于深度优先搜索的正方化树图布局算法①

刘旭

(SAP中国研究院 商务智能部,上海 201203)

正方化布局算法在树图可视化形式中得到广泛使用,然而经典正方化树图布局算法无法获得平均长宽比最优的结果.通过分析经典正方化树图布局算法的实现细节,特别是每一步矩形块位置的选择过程,论证了经典正方化算法由于使用贪心算法原理导致的缺陷,结合深度优先搜索技术,提出了基于深度优先搜索的正方化树图布局算法(DSS算法).在详细阐述DSS算法实现过程的基础上,结合实证研究,对DSS算法在平均长宽比方面的优势,时间性能的改进方向和本质特点进行了深入探讨.

可视化;树图;正方化;深度优先;搜索

层次数据的常见可视化形式是树形图,然而树形图的连接线段之间存在大量空白无法利用,当数据量增加时,子结点会逐渐密集排列在一起,从而难以区分.Treemap(树图)使用具有一定面积的块来表示数据结点,而利用结点之间的位置关系来表示数据之间的层次关系[1].相对于树形图,Treemap的优点是充分利用了空间[2],可以通过结点的大小,颜色表示数据的各种属性[3],同时,Treemap的结点位置还可以表示数据的分布关系[4].

Treemap的基本形式是用一个矩形区域表示根结点,将根结点划分为多个矩形区域以表示子结点,这样递归地表示整个层次结构数据[5].图1描述了一个Treemap的生成步骤[6].基本布局算法是Treemap绘制过程中必须首先解决的问题.由于Treemap是一个递归结构,要实现一个Treemap的布局算法,最关键的问题就是实现单层Treemap子结点的布局,也即在给定结点权重和结点序列的情况下,确定在二维的平面上排布矩形的方案[7].不同的排布方案会产生不同的可视化效果.

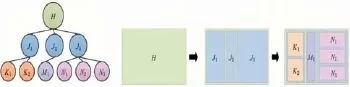
图1 Treemap的生成步骤[5]

在Treemap的主要布局算法中,以生成平均长宽比较小的矩形为目标的经典正方化(Squarified)算法有广泛的应用[8],但是此算法所使用的贪心算法原理令其在很多情况下无法获得最优解,有些时候获得的结果与最优解差距较大.如果在经典正方化算法的基础上加入搜索技术,可以给出一种改进的算法获得更优结果.

1 经典正方化算法的实现细节

如果Treemap布局中划分出大量细长的小矩形,则难以进行辨认和鼠标点击.为了解决这个问题,需要有一种布局算法降低生成矩形的平均长宽比,经典正方化算法就是为了这一目的而提出的.如果要获得平均长宽比最低的结果,此问题是一个NP难问题,但是在实际情况中,只需要得到一个平均长宽比相对较低的结果[9].

经典正方化算法是贪心算法的应用,其思路是首先将子结点按从大到小排序,然后从第一个结点开始,按照从短边开始的策略填充.从第二个矩形开始,当填充第i个矩形时,在当前的Row(即当前行列)中插入或者新建Row这两种策略中选择,而选择的依据是第1至第i-1个已经填充矩形的最高长宽比或平均长宽比,最高长宽比或平均长宽比较低的填充策略则为第i个结点的填充方式[10].如果用伪代码描述,经典正方化算法为:

图2是经典正方化算法的一个示例[8],使用的排序后的序列为6,6,4,3,2,2,1.可以看出此算法可以得到平均长宽比较低的布局.

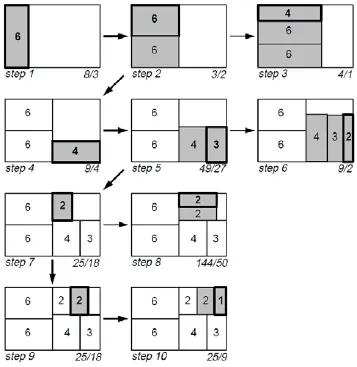
图2 经典正方化算法示例[8]

对于经典正方化算法,首先要进行排序,使用归并排序的最坏时间花销为O(nlogn),然后,要进行n个步骤,每一步需要计算当前的行或列的平均长宽比.在最坏情况下,所有的矩形都放置于初始的行或列中,则算法在选择策略上的时间花销为0+1+2+…+(n -1)=n(n-1)/2,故在最坏情况下,经典正方化算法的时间性能为O(n2),可以看出此时间性能是可以接受的[11].

2 对经典正方化算法缺陷的分析

在对经典正方化算法进行大量的测试之后,易知该算法在大多数情况下获得的结果令人满意,但是在有些情况下获得的结果明显较差.图3显示的是一个无法获得最优解的典型情况,给定的矩形是一个长宽各为100的正方形,需要放入的三个矩形块序列为[4800,4800,400].图3(a)显示的是一个较优解,此布局下的各矩形平均长宽比为3.5395,然而使用经典正方化算法只能获得图3(d)所示的结果,此布局下的各矩形平均长宽比为9.6133,从图中可以明显看出最后一个矩形长宽比很大,视觉效果不佳.

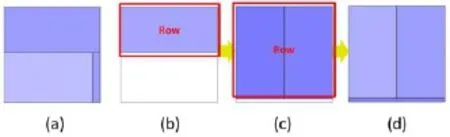
图3 经典正方化算法对于[4800,4800,400]不能获得最优解的情况

出现这种情况的直接原因在于,经典正方化算法在对第二个矩形块布局时选择了插入已有的Row,而不是新建Row.如图3(b)所示,在放入第二个矩形块时,当前的Row中有第一个矩形,容易算出,此时插入当前Row的两个矩形平均长宽比为1.92,而新建Row之后两个矩形的平均长宽比为2.0833,故按照贪心算法的原理应该选择如图3(c)所示的那样插入当前Row,但是,在对第三块矩形布局时,不管是插入现有的Row还是新建Row,都会成为一个狭长的矩形,导致最终所有矩形块的平均长宽比反而不如在第二块矩形新建Row,并在第三块插入第二块新建的Row所获得的图3(a)所示的效果.

通过进一步分析布局过程,可知按照经典正方化算法对序列元素逐个布局的方式,为了取得较小的平均长宽比,对每一个新加入的矩形块实际上有三种可能的布局方式:(1)插入当前的Row(插入的方向由当前Row的方向确定);(2)在空白区域靠短边新建Row; (3)在空白区域靠长边新建Row[12].由于经典正方化算法只保证已经加入的矩形块具有最小的平均长宽比,不考虑未加入的矩形块,这意味着经典正方化算法会错过那些对于已经加入的矩形块不利,但是对未来新加入的矩形块有利的布局.例如在图3所示的情况下,第二个矩形块应该是新建Row比插入当前Row更加有利.特别地,经典正方化算法不会在空白区域靠长边新建Row,因为对于当前Row中的矩形块而言肯定是靠短边较优,但是在有些情况下靠长边新建Row反而对未来的矩形块有利.

图4显示了一种靠长边新建Row更好的典型情况,矩形空间长为400,宽为300,需要放入的矩形块序列为[400,400,100,100,100,100],图4(a)显示的是最佳布局方案,此时所有的矩形块都是正方形,平均长宽比为1,但是使用经典正方化算法只能得到图4(b)所示的结果,易知此时所有矩形块的平均长宽比为1.7778.图5详细分析了导致这种结果的原因.为了得到最佳布局方案,第一块矩形新建Row时应该选择靠长边,这样第二块矩形加入Row之后即可获得两个正方形的矩形块.但是经典正方化算法的特点是在加入第一个矩形块时不考虑第二块,故对第一块矩形新建Row时选择的是靠短边,这样开始的两个矩形块就错过了选择最佳方案的机会,之后的矩形块无论是插入Row还是新建Row,第一块矩形的长宽比都不可能达到1.

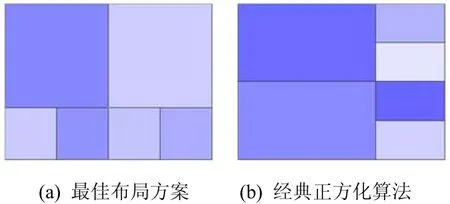
图4 经典正方化算法对于[400,400,100,100,100, 100]不能获得最优解的情况

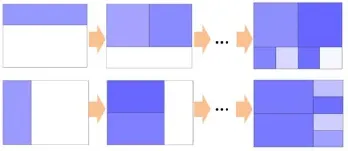
图5 靠长边新建Row获得更优布局的步骤分析

3 完整搜索的DSS算法

从以上的分析可以看出,为了获得更优结果,在每一步选择布局方案时不仅需要考虑当前矩形块的平均长宽比,还要探测后继矩形块的布局情况,探测的矩形块越多,越可能选择出更优结果.理想情况下,检查了所有矩形块布局方案之后就可以获得在逐步靠边新建Row的这一算法框架下的最优解.

为了探测所有可能的布局情况,算法中需要引入搜索技术,以当前的布局方案为基点扩展搜索树．搜索树的扩展方式有多种,但最基本的是广度优先和深度优先两种方式．在搜索方式的问题解决过程中,一般在搜索树的某些分支深度可能无限,或是搜索结果可能在浅层结点出现时会优先考虑广度优先搜索.然而就当前问题而言,搜索树的深度是有限的,搜索层数一定要达到最深才能获得搜索结果,这意味着深度优先搜索具有和广度优先搜索一样的完备性,而且使用广度优先搜索也不可能在较浅的搜索层次上提前获得搜索结果.使用广度优先搜索的缺点在于需要维护一个先进先出的队列保存搜索树状态,算法会有较高的空间复杂度[13].

如果使用深度优先搜索,由于已经搜索过结点的所有后代结点都可以不再保存,需要保存的搜索树状态大大减少.搜索树的状态需要记录在栈中,如果使用JavaScript等高级语言,间接递归的程序设计方式即可很简明的实现搜索栈,同时,深度优先搜索在这个问题上的另一个优势是如果有一条搜索路径搜索到所有矩形块均为正方形的方案,例如出现图4(a)所示的情况,即可直接结束搜索,广度优先搜索在获得这一结果之前必须探测所有的较浅层结点,需要检查的结点数量比深度优先搜索多.如果在经典正方化算法的基础上加入深度优先搜索技术,可以得到基于深度优先搜索的正方化算法(Depth-first Search Squarified算法,简称DSS算法),此算法可以有效地改进最终布局结果.

如果使用JavaScript伪代码,一个完整搜索所有布局方案的DSS算法可以用以下函数表示:

DSS算法的执行需要调用 DSSquarify函数, rectObjs是当前用于布局的数组,itemIndex是指当前用于布局的数组元素索引,在初始状态下为 0, currentRowRect表示当前的Row,初始状态下长宽都是0,currentLiveRect表示当前未被填充的矩形空间. evaluateAspectRatio函数用于计算当前布局方案的所有矩形平均长宽比,计算之后获得的newCtx_inRow, newCtx_newRowShort,newCtx_newRowLong包含有完整的布局方案.DSSquarify函数实际上就是比较三种方案的平均长宽比,用min函数选择平均长宽比最低的值,然后返回最低值对应的布局方案. evaluateAspectRatio函数为了计算出所有矩形块的平均长宽比,需要完成整个布局过程. evaluateAspectRatio函数的伪代码如下:

可以看出,evaluateAspectRatio函数的执行过程实际 上 是 先 调 用 insertAndLayoutRow 或 者makeNewRowAndLayout函数按照不同的方案摆放当前的矩形块,然后递归地调用缩小了问题规模的DSSquarify函数完成剩下矩形块的摆放,最后进行对于当前方案的估值.其中的insertAndLayoutRow是当前矩形块插入当前 Row 的布局过程,而makeNewRowAndLayout是当前矩形块新建Row的布局过程,参数isLongFirst指定了Row是靠长边还是靠短边.在调用DSSquarify完成了剩下的矩形块布局之后,evaluateAspectRatio函数调用evaluateAllRects完成对于当前布局方案的估值,估值的过程就是计算所有矩形块的平均长宽比.

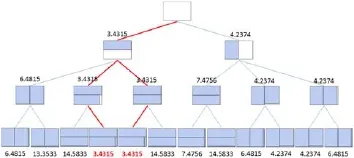
图 6 完全搜索的DSS算法执行示意图

图6 用树形图直观显示了完全搜索的DSS算法的一个执行过程,其中矩形空间长为150,宽为100,需要放入的矩形块序列为 [48,48,4].可以看出,DSS算法一共进行了三层搜索,搜索的过程就是以深度优先的方式遍历整个树形结构,并在叶子结点进行估值计算,而每一个父结点的估值都是由最小的叶子结点估值决定的.一般而言,在每一层搜索都有三种可选的方案,只有第一层和最末层是例外(以叶子结点为搜索的最末层),由于在最末层只剩下一个矩形块,只有插入Row和填充全部空白新建Row这两种摆放方式,而在第一层,由于Row还没有建立,不存在插入Row的摆放方式,仅能以两种不同方式新建Row.从图中可以看出,红线加粗的两种方案的最终估值均为3.4315,为各种方案中最小值,而这两种方案的第一步都是靠长边新建Row,这是使用经典正方化算法无法获得的结果.

4 对完整搜索的DSS算法的改进

完整搜索的DSS算法似乎已经在通过新建Row来逐步完成布局的框架下给出了一个最优的解决方案,然而,完整搜索的DSS算法是缺乏实用价值的,其最大的问题在于时间性能.根据上文的分析,在一般情况下,每一层搜索都有三种可能的布局方式,即使假定每一层的布局时间开销为常数,完成n个矩形块的布局搜索需要的时间也高达O(3n),这是指数时间的算法,实际上每一层布局的时间还与n有关,在运行中,时间开销会随着n的增大迅速增加,因此该算法一般不能用于实际应用程序.JavaScript语言兼具面向对象和函数式编程风格,已经在可视化软件开发中得到广泛应用[14].如果应用程序使用JavaScript编制并运行于Chrome中,当n=20时,完整搜索的DSS算法在一台CPU为Intel Core 2 Duo 2.20GHz的个人电脑上的运行时间已经超过6秒,这样的性能是令人无法接受的.

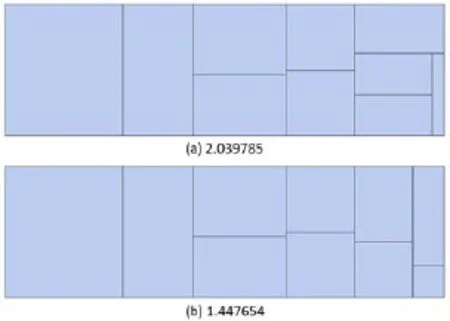
图7 经典正方化算法和完整搜索的DSS算法布局比较

由于时间的开销是由于搜索层数的增加,为了改进完整搜索的DSS算法,一个最直观的策略就是减少搜索层数,即指定一个搜索层数S,每次搜索时仅搜索当前位置开始的S层,在还没有对所有矩形块完成布局的情况下,使用已经完成布局的S层矩形块进行估值.如果以N表示矩形块个数,可见完整搜索的DSS算法中S=N,而经典正方化算法即为S=1的DSS算法.减少搜索层数实际上是一种质量和效率的折衷,其优点是可以显著加快算法运行速度,但也使得估值结果不够准确,从而可能无法获得完整搜索的DSS算法可以获得的最优方案.另一个提高时间性能的策略是在开始进行较少层次的搜索,仅在最后L层进行完全搜索.图7显示的是在矩形空间长为100,宽为30的情况下,分别使用经典正方化算法和完整搜索的DSS算法对序列[3366,1857, 5437,2668,3867,1920,2695,9192,2605,583]进行布局获得的结果,其中的2.039785和1.447654是两种布局方案的平局长宽比.可以看出,完整搜索的DSS算法获得的结果较优,但是两种算法对于开始的6个矩形块的布局方案是完全一样的,区别仅在于最后4个矩形块布局的不同,尤其是最后一个矩形块.这一现象的出现不是偶然的,而是经典正方化算法的贪心原则导致的.在布局的开始阶段,由于剩下的矩形块个数较多,长宽比例较大的矩形块还可能在后续的布局中得到调整,但是对于后续的矩形块,调整的机会越来越少,从而最后的几个矩形块布局方案往往较差,影响了所有矩形块的平均长宽比.通过对经典正方化算法生成的大量布局方案进行统计,可知在超过85%的情况下,长宽比最高的那个矩形块出现在最后10%的矩形块中.

既然经典正方化算法的弱点主要集中在最后的几个矩形块,仅在最后L层进行完全搜索即可在时间代价较小的情况下获得较优的布局,例如,仅需搜索最后两层即可避免图3示意的对于[4800,4800,400]不能获得最优解的情况.在引入S作为搜索层数和L作为最终完全搜索层数这两个参数之后,可以获得一般形式的,更加具有实用价值的DSS算法,可根据实际的硬件水平和应用场景选择合适的S和L.一般情况下,在DSS算法的运行中取S=1,L=6即可获得时间性能较好,同时明显优于经典正方化算法的结果.在这里也不难看出,完全搜索的DSS算法和经典正方化算法实际上都是DSS算法的两个特例,在完全搜索的DSS算法中S=N,L=N,而在经典正方化算法中S=1,L=1.

5 实验和进一步分析

在具有实际意义的信息可视化过程中,过大的N值往往会导致多数显示的矩形块面积过小而难以看清,故一般会采用适当的数据聚合方式以使N的值不会很大,N在100之内的情况比较常见.普通用户对于图形渲染可接受的等待时间一般在3秒之内,考虑到硬件的发展,在实验中认为6秒是DSS算法最大可接受运行时间.

表1列出了DSS算法在不同的S值和L值下运行的实验结果,实验的硬件条件是一台CPU为Intel Core i7 2.93 GHz,内存16GB的个人电脑,软件环境是Windows 7企业版,DSS算法使用JavaScript实现,运行于Chrome浏览器.表格中的实验结果都是取随机数运行100次之后的平均值,其中N代表矩形块的个数,时间的单位是毫秒,S=1,L=1即为经典正方化算法,S=N,L=N为完整搜索的DSS算法,标记为N/A的单元格表示因为需要的运行时间超过6秒(6000毫秒)而不予统计结果.

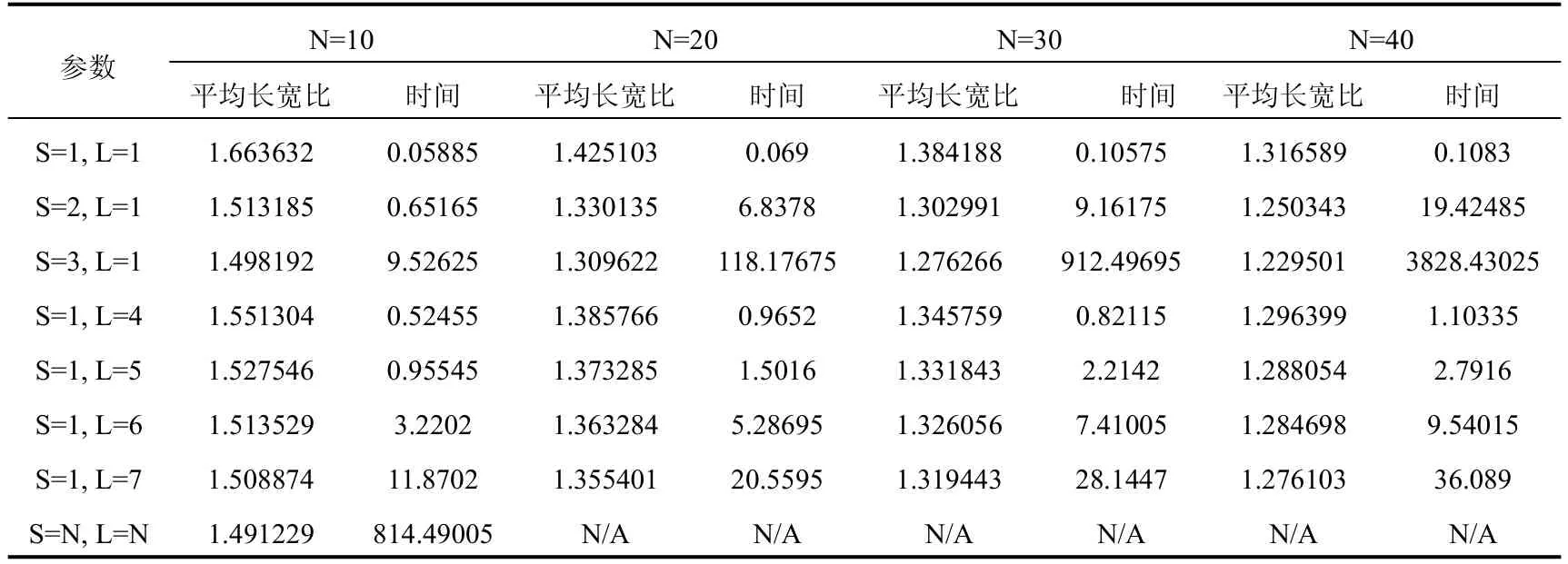
表1 DSS算法在不同参数下运行的实验结果

通过实验数据不难看出,S值和L值越大,平均长宽比越低,但是需要的时间也越长.为了进一步分析表格中的数据,可以使用可视化的方式对平均长宽比和时间的变化分别生成折线图.图8显示了平均长宽比变化的折线图,从图形可知平均长宽比随着N的增加而降低,而S和L对于平均长宽比的影响在N较小时更加显著.这说明在使用DSS算法时,可以在问题规模较小(N较小)时使用较大的S和L值以获得更优结果,由于问题规模小,付出的时间代价有限,而在问题规模较大时,由于平均长宽比会降低,可以适当减小S和L值以获得更优的时间性能.

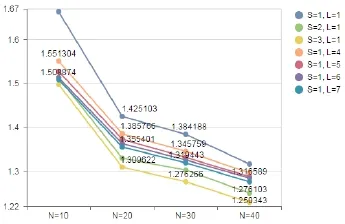
图8 平均长宽比变化折线图

图9 显示的是运行时间随S值和N值变化的折线图.从图中可以看出时间的消耗对S值的变化高度敏感,S较大时,运行时间随N值增长很快,近似于指数曲线,这是由搜索算法的特点决定的.在L=1,N=40的情况下,S=3时算法需要的执行时间是S=2时的将近200倍,接近4秒.在实际的应用中,一般不宜取较大的S值.

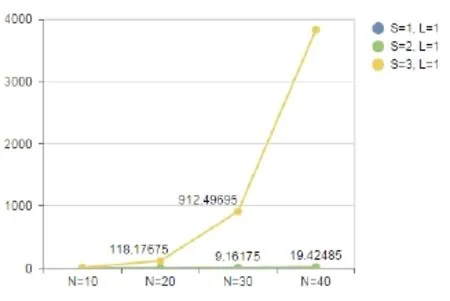
图9 运行时间随S值和N值改变的折线图

图10显示的是运行时间随L值和N值变化的折线图.不难看出,当L值变大时,运行时间随N的增长率也变大,但是增长的趋势比较平缓,近似于线性.在实际的应用中,可以考虑取L=6或L=7.

为了提升DSS算法的时间性能,除了选择适当的S和L值之外,还可以考虑更多策略,例如在搜索过程中引入启发式规则,以及使用空间换时间的策略缓存和重复利用中间估值结果.启发式规则在许多深度优先搜索算法中常用,一般是一些经验规则,例如在搜索到一个父结点时,在已经完成布局的矩形块中如果出现长宽比大于10的情况,则停止搜索该结点的所有子结点,并为该结点估值为无穷大.启发式规则可以有效降低搜索时间的消耗,但也有可能错过一些开始布局较差但后续布局较好的方案.在对布局方案的搜素过程中,有可能出现重复的布局情况,例如在图6中的第三层即出现了好几对重复布局.如果之前的布局估值已经被缓存,则在出现重复布局时,如果重复的布局不是最末层结点,就可以避免对子结点的重复搜索,仅需返回已缓存的估值即可.重复利用中间估值结果的方案关键需要是实现快速的布局比较和合适的缓存结构[15].

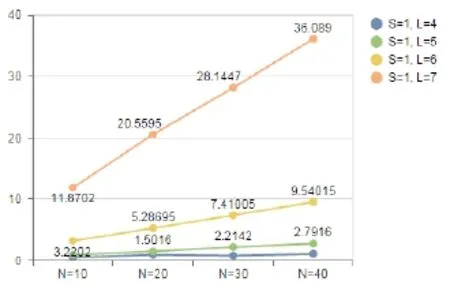
图10 运行时间随L值和N值改变的折线图

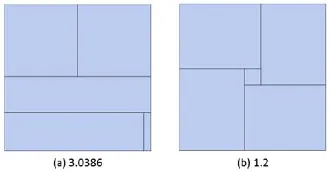
图11 使用完整搜索DSS算法不能获得数学上最优解的情况

此外,必须提到的一点是,在矩形空间中对若干矩形块布局是一个NP难问题,要获得数学意义上的最优解非常困难.DSS算法的实现仍然沿用了经典正方化算法的基本思路,即逐块矩形不断靠边新建Row或插入已有的Row,将空白区域保留在靠矩形空间角落的地方,这一思路是无法涵盖所有可能的布局的.即使是完整搜索的DSS算法,在某些情况下获得的依然不是数学意义上的最优解.例如图11显示的情况,矩形空间长宽均为9,矩形块序列为[20,20,20,20,1],图11(a)显示的是完整搜索的DSS算法获得的布局,平均长宽比为3.0386,但是图11(b)是一个显然的更佳布局,平均长宽比仅为1.2,然而,图11(b)的这一布局是不可能通过DSS算法搜索到的,因为最后的小矩形块不被保留在矩形空间的任何一个角落上.

6 结论

DSS算法是在对于Treemap的经典正方化布局算法进行深入分析的基础上提出的,从本质上来说,它是对经典正方化布局算法的一种扩展,以更多的时间和空间换更优解,即通过对于搜索状态树上更多结点的探测获得更佳的布局结果.DSS算法中的参数,本质上是算法性能和更优结果之间的一种折衷,而经典正方化布局算法实际上就是DSS算法的一个时间与空间代价最小,然而布局效果最差的特例.在实际应用中,需要结合实际情况使用最适合当前应用场景的参数设置,也可考虑使用启发式规则和缓存技术进一步改进DSS算法.从工程的角度来说,DSS算法已经明显改善了经典正方化算法的布局结果,但是如果要获得数学意义上的最优结果,仍然需要更多探索.

1 Bederson BB,Shneiderman B,Wattenberg M.Ordered and quantum treemaps:Making effective use of 2D space to display hierarchies.ACM Trans.on Graphics(TOG),2002, 21(4):833–854.

2 Chintalapani G,Plaisant C,Shneiderman B.Extending the utility of treemaps with flexible hierarchy.Proc.Eighth International Conference on Information Visualisation, 2004(IV 2004).IEEE.2004.335–344.

3 Vliegen R,Van Wijk JJ.Visualizing business data with generalized treemaps.IEEE Trans.on Visualization and Computer Graphics,2006,12(5):789–796.

4 Balzer M,Deussen O,Lewerentz C.Voronoi treemaps for the visualization of software metrics.Proc.of the 2005 ACM Symposium on SoftwareVisualization.ACMF.2005.165–172.

5 Tu Y,Shen HW.Visualizing changes of hierarchical data using treemaps.IEEE Trans.on Visualization and Computer Graphics,2007,13(6):1286–1293.

6陈谊,胡海云,李志龙.树图布局算法的比较与优化研究.计算机辅助设计与图形学学报,2013,25(11):1623–1634.

7张昕,袁晓如.树图可视化.计算机辅助设计与图形学学报, 2012,24(9):1113–1124.

8 Bruls M,Huizing K,Van Wijk JJ.Squarified treemaps. Springer.2000.

9谷建涛,周哲,曹建亮.基于正方化算法的树图生成方法研究.计算机应用与软件,2008,25(7):74–76.

10 Shneiderman B,Wattenberg M.Ordered treemap layouts. IEEE Symposium on Proc.of the Information Visualization. IEEE Computer Society.2001.73.

11 Engdahl B.Ordered and unordered treemap algorithms and their applications on handheld devices[Master’s Thesis]. Department of Numerical Analysis and Computer Science, Stockholm Royal Institute of Technology,2005.

12周哲.双向正方化树图生成算法[硕士学位论文].长沙:湖南大学,2005.

13 Russell SJ,Norvig P,Canny JF,et al.Artificial intelligence: A modern approach.Prentice hall Upper Saddle River, 2003.

14刘旭.ChromeV8引擎中的JavaScript数组实现分析与性能优化.计算机与现代化,2014,(10):66–70.

15 Tamassia R.Handbook of graph drawing and visualization. CRC press,2013.

Squarified Treemap Layout Algorithm Based on Depth-First Search

LIU Xu

(Department of Business,Intelligence of SAP Labs China,Shanghai 201203,China)

Squarified layout algorithm is widely used in the Treemap Visualization,but classic Squarified algorithm cannot achieve the best average aspect ratio.By analyzing implementation details of Squarified Treemap layout algorithm,especially each step of the rectangular block position selection process,the paper demonstrates the drawback of classic Squarified algorithm caused by using greedy algorithm.Combining with depth-first search technique,it also proposes Squarified Treemap layout algorithm based on depth-first search(DSS algorithm).Based on elaborating implementation process of DSS algorithm,combining empirical research,the advantage of the DSS algorithm in the aspect ratio,the improvement direction and the essential characteristics of the time performance are discussed.

visualization;treemap;squarified;depth-first;search

2016-08-02;收到修改稿时间:2016-09-27

10.15888/j.cnki.csa.005734